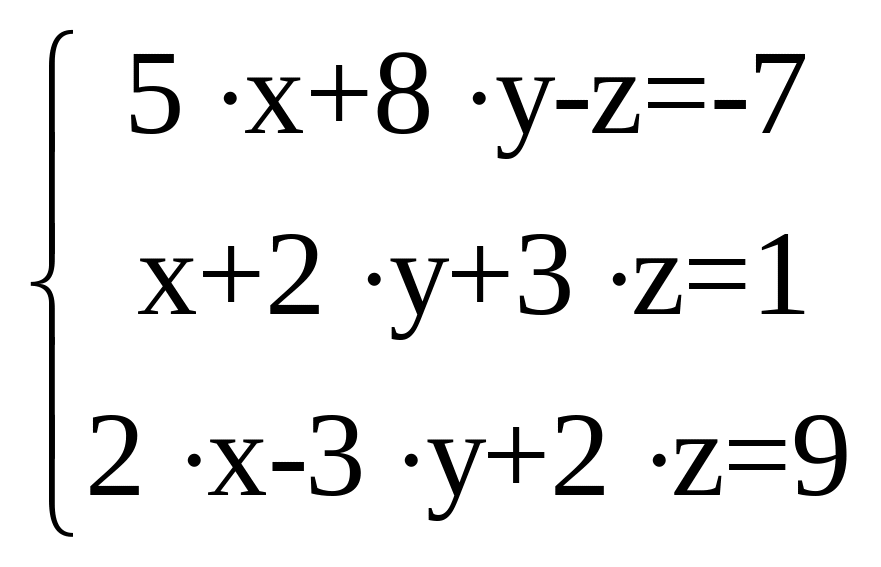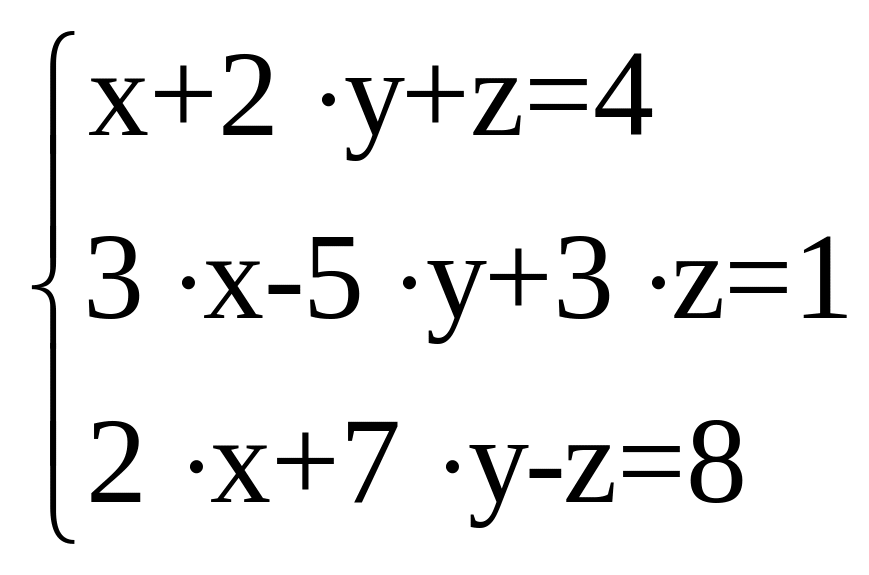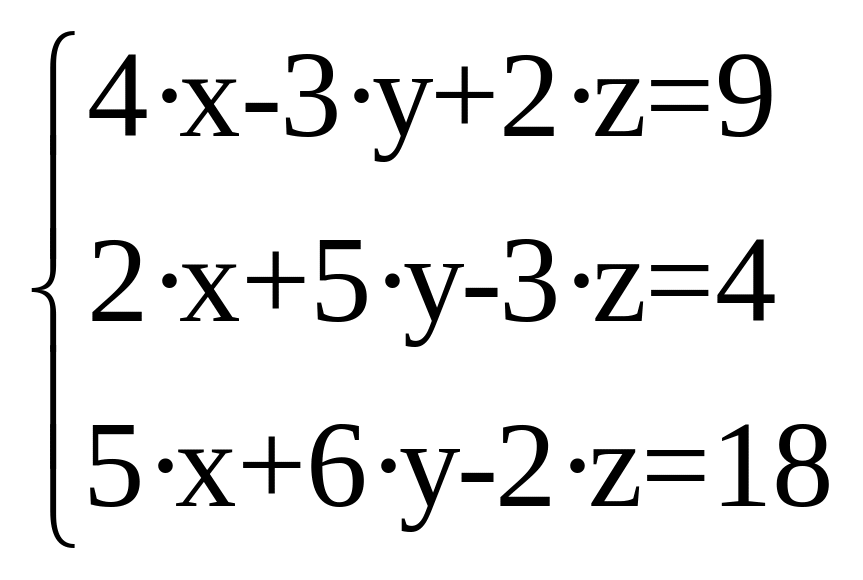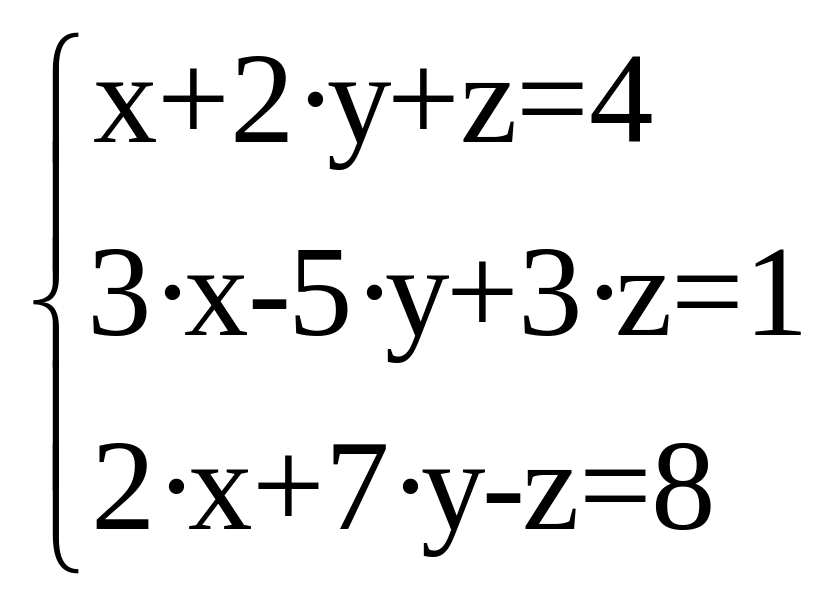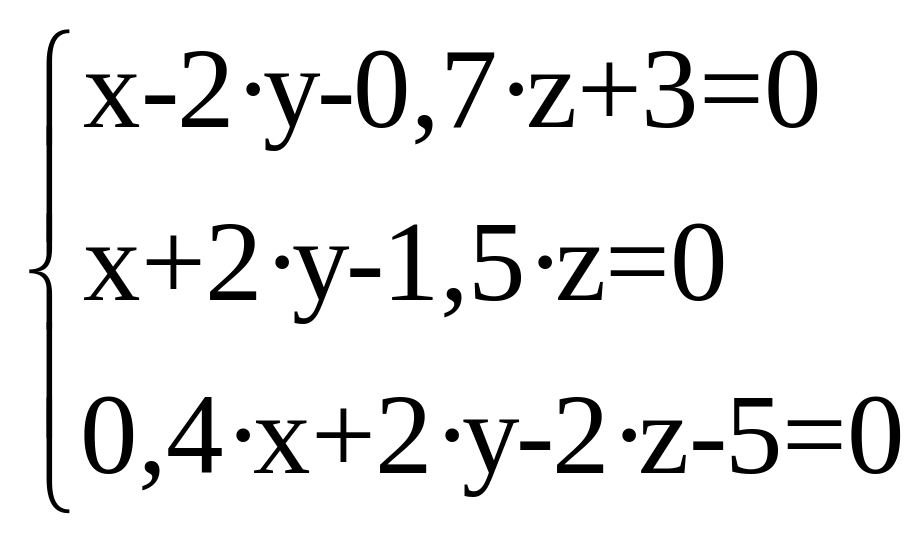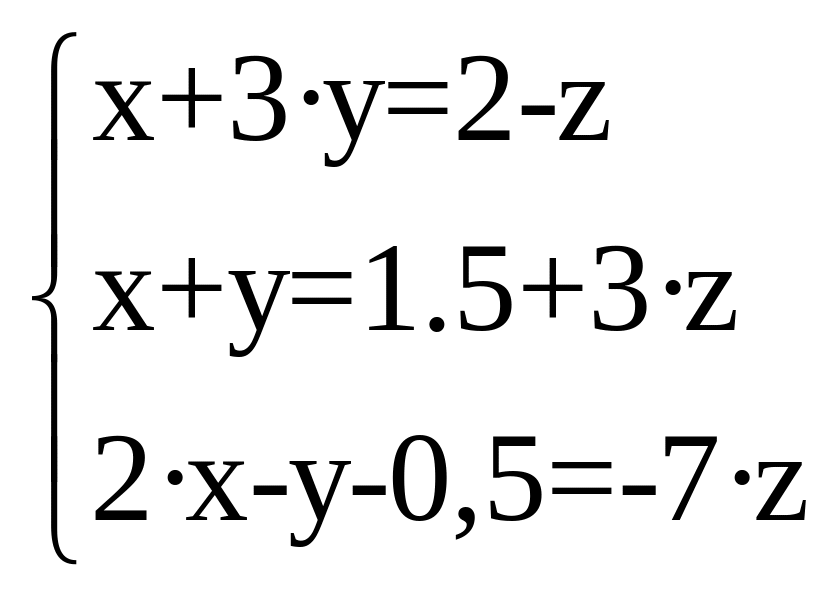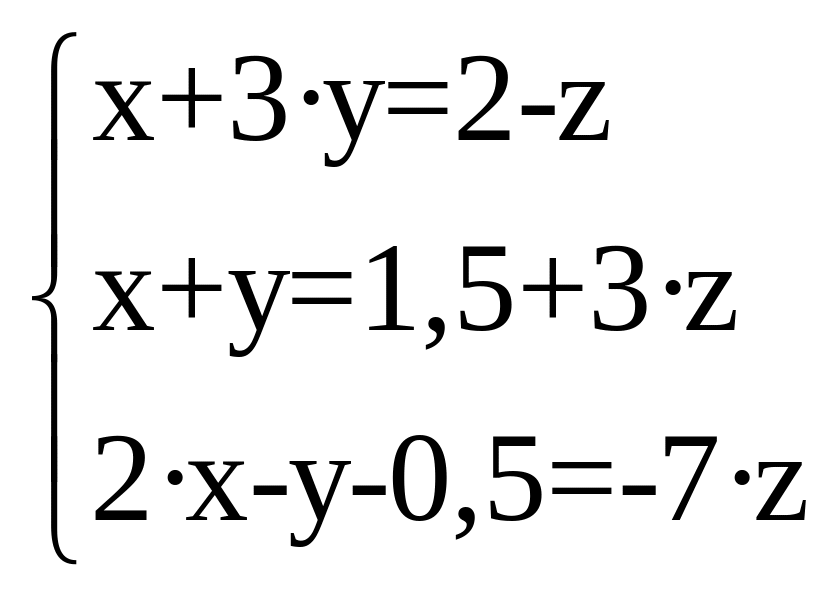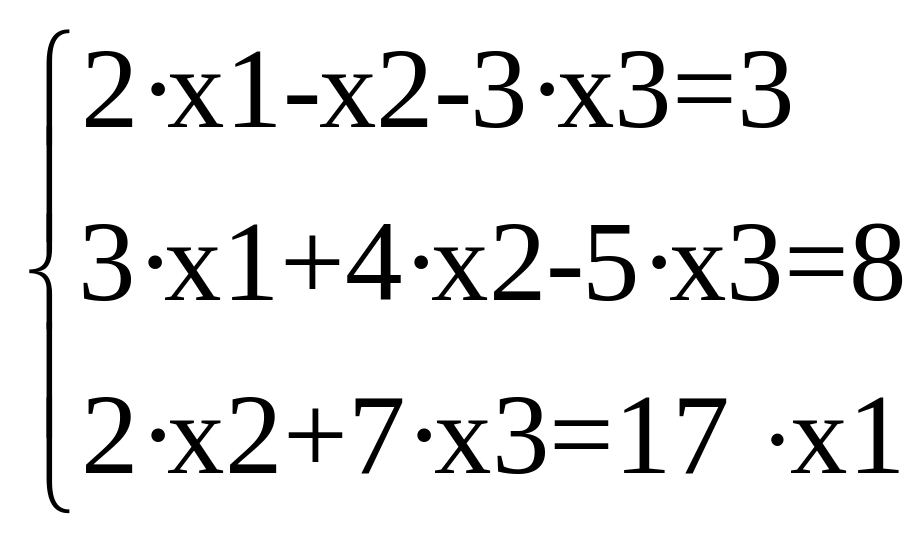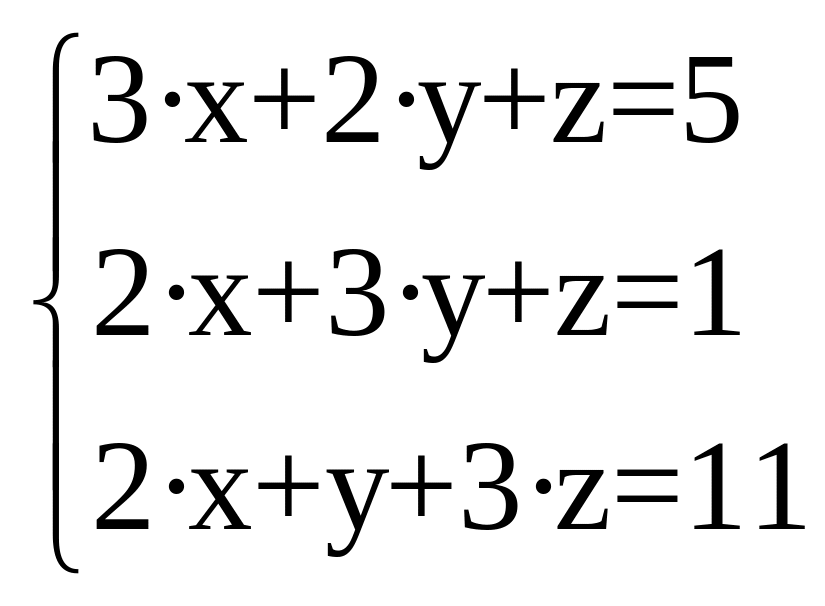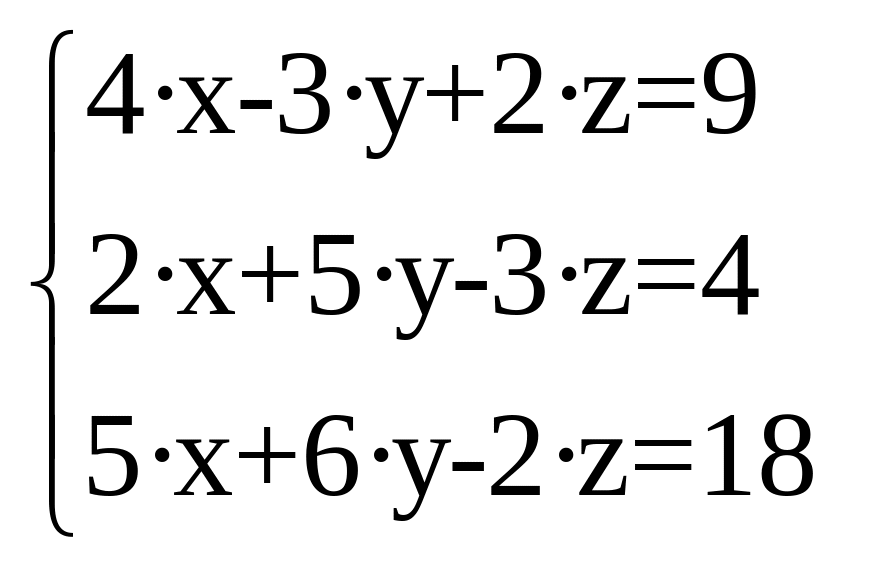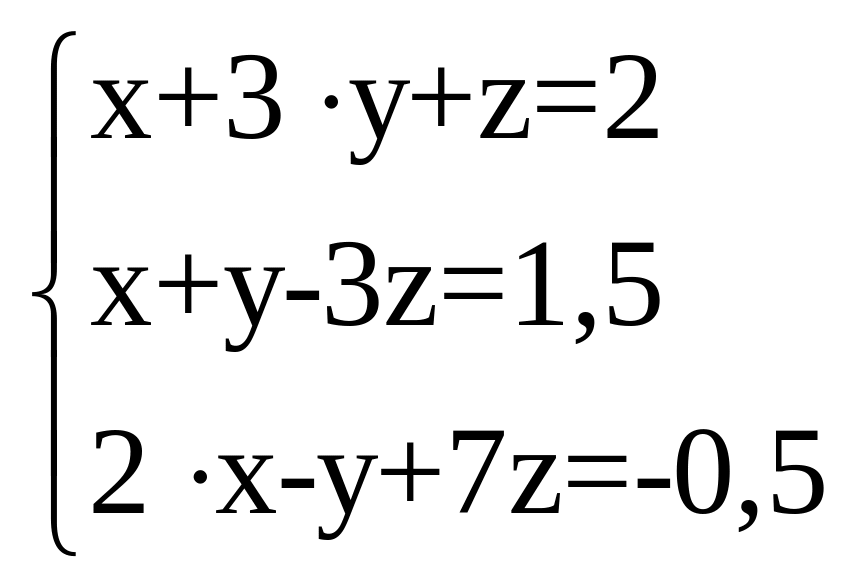2. С помощью преобразованной (обратной) матрицы

Для поиска решения системы уравнений используем соотношение: ,

где: M – матрица системы уравнений; – преобразована (обратная) матрица; V – вектор правых частей уравнений; VX – вектор неизвестных.

Последовательность вычисления

1. Запишите уравнение в матричной форме:

• матрица коэффициентов – ячейки A3:C5;

• вектор правых частей уравнений – ячейки G3:G5.

2. Преобразуйте матрицу коэффициентов (вычисление обратной матрицы) – ячейки A8:C10.

3. Умножьте обратную матрицу на вектор правых частей уравнений.

В результате будет получен вектор, элементы которого являются искомыми неизвестными, – ячейки G8:G10.

Совет. Для получения обратной матрицы и вычисления произведения матриц (матрицы на столбец) используйте функции из категории «математические».

Результаты решения системы приведены ниже.

3. Решение системы уравнений с помощью надстройки «Поиск решения»

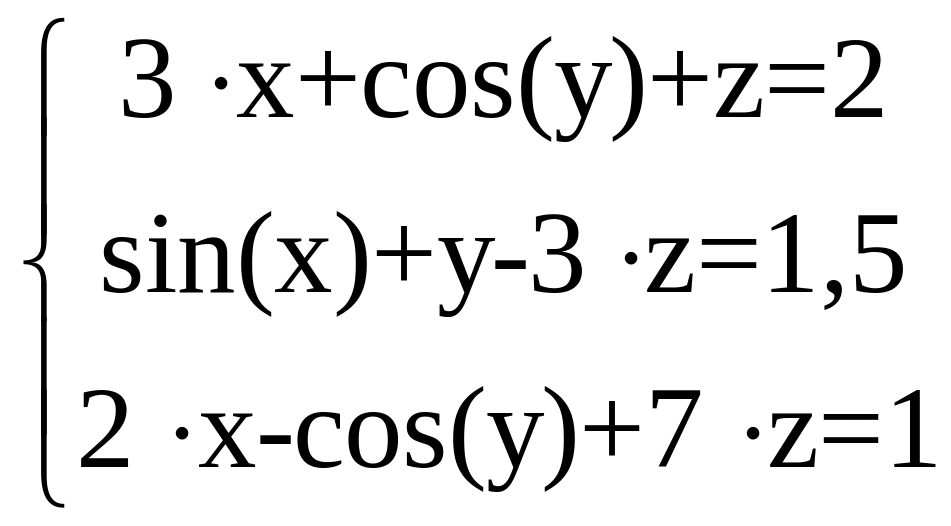
• Для поиска значений x, y и z, при которых F(x)=0 составьте функцию:

• Задайте начальные приближения для переменных x, y, z, введя в ячейки необходимые значения, например 1 (A3→1, B3→1, C3→1, по умолчанию начальные приближения равны 0).

• В ячейку D3 введите формулу, которая определяет значение функции F.

• Откройте диалоговое окно «Поиск решения» и задайте сценарий решения (см. ниже).

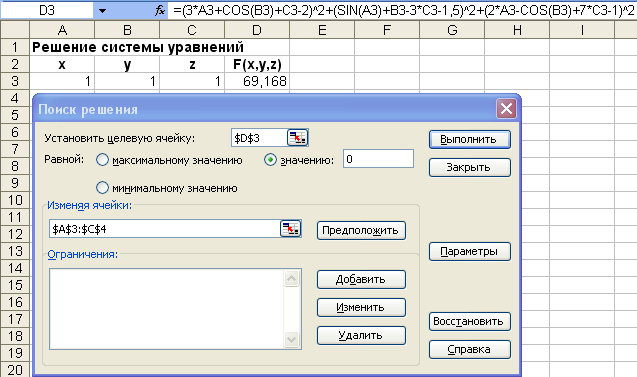
• Нажмите кнопку Выполнить (Solve), получаем решение x=0,516841 (значение в ячейке A3), y=1,161748 (значение в ячейке B3), z=0,052001 (значение в ячейке C3), а в ячейке D3 значения функции.

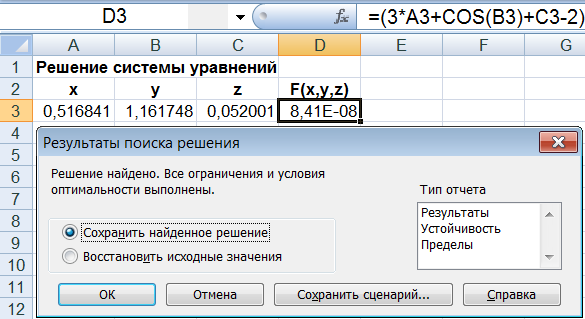
• Нажмите OK для сохранения результатов на листе. Если нужен отчет, воспользуйтесь полем Тип отчета (Reports), для выбора типа отчета: Answer – Результаты; Sensitivity – Устойчивость; Limits – Пределы.

Среда пакета Mathcad

3. Выполнить указанные ниже операции с векторами и матрицами

Построить матрицу М по заданным уравнениям (см. табл. 2), найти максимальный элемент N-го столбца (вектора V) и минимальный элемент матрицы.

Выполнить такие действия:

• получить матрицу M1 (транспонировать матрицу M)

• вычислить сумму элементов N-ой строки матрицы М1.

• построить вектор V (N-ый столбец матрицы M1)

• объединить вектор V с матрицей М.

• суммировать матрицы М и М1.

• найти сумму элементов матрицы, полученной после суммирования.

Последовательность выполнения задания достаточно полно проиллюстрирована на листинге, который приведен ниже и дополнительных пояснений не требуется.

Среда пакета Mathcad

4. Использовать встроенные функции пакета для работы с файлами

1. В любой среде программирования написать программу вычисления элементов вектора V и матрицы M по заданным формулам (смотри таблицу 2), со последующим выводом полученных данных в файл последовательного доступа.

Построение вектора и матрицы можно выполнить с помощью какого либо текстового редактора, или в любой другой среде, например Mathcad, Excel, или с консоли, набрав последовательно их элементы (задавая произвольно), разделяя запятыми, с последующим сохранением в файле.

Для исключения возможных ошибок при обращении к файлу его имя должно иметь расширение .prn (или .dat, .txt).

Внимание! Для исключения ошибок при выполнении операций с векторами и матрицами количество элементов в векторе должно равняться количеству элементов в столбце матрице.

2. Прочитать данные файла (вектора и матрицы), и последовательно выполнить операции, которые приведены на листинге ниже.

Последовательность выполнения задания достаточно полно проиллюстрирована фрагментом документа приведенного на листинге и отдельных объяснений не требует.

Внимание! В приведенном документе вектор и матрица построены непосредственно в среде пакета Mathcad.

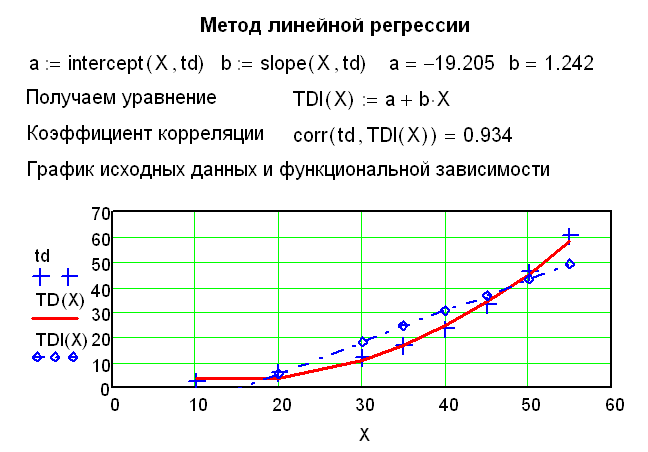
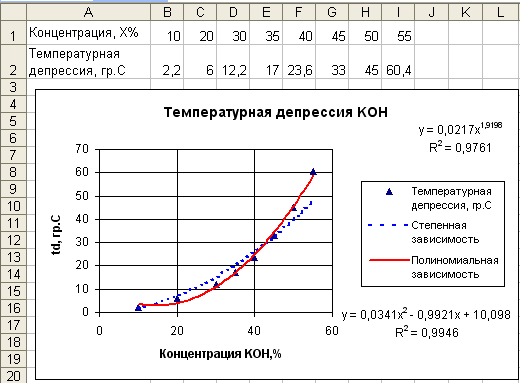
5. По данным эксперимента (или табличным данным) определить функциональную зависимость

Построить матрицу исходных данных, выбрать вид кривых (два варианта) и определить коэффициенты функциональных зависимостей, которые описывают экспериментальные данные с ошибкой ±5%, построить графики исходных данных и функции.

Выполнить проверку и анализ представления экспериментальных данных полученными зависимостями (определить коэффициенты корреляции).

Среда пакета Mathcad

Совет. Для аппроксимации с высокой точностью можно воспользоваться и другими функциями Mathcad, например:

linfit – аппроксимация линейной комбинацией функций;

genfit – аппроксимация нелинейными функциями и др.

Среда пакета Excel

Список рекомендуемой литературы

1. Коцаренко В.О., Селихов Ю.А. Обчислення у MATHCAD. Навч. посіб./ – Х.: НТУ «ХПІ», 2011. – 200 с.

2. Коцаренко В.А., Иванов В.А., Соловей Л.В. Методические указания к выполнению лабораторных работ и расчетных заданий (Инженерные расчеты в среде Excel). – Харьков: НТУ „ХПИ”, 2006. – 104с.

3. Коцаренко В.О., Селихов Ю.А., Горбунов К.О. Розрахунки у середовищі Excel : навч. посіб.  – Х.: НТУ «ХПІ», 2011 . – 270 с.

4. Ларсен Рональд У. Инженерные расчеты в Excel.: Пер. с англ. – М.: Издательский дом “Вильямс”, 2002. – 544 с.

5. Кирьянов Д.В. Mathcad 13. – Спб.: БХВ – Петербург, 2006. –590с.

Приложение 1. Титульный лист

Министерство образования и науки, молодежи и спорта Украины

Национальный технический университет

“Харьковский политехнический институт”

Кафедра интегрированных технологий, процессов и аппаратов

РАСЧЕТНОЕ ЗАДАНИЕ (КУРСОВАЯ РАБОТА)

курс «Информатика»

вариант №

Студента (ки):

Группа:

Преподаватель:

Расчетное задание

(Курсовая работа)

защищено с оценкой:

Харьков 2011

Приложение 2

Л И С Т З А Д А Н И Я

1. Выполнить исследование функции: .

Построить график функции в диапазоне Х=1 15 (шаг изменения переменной X равняется 0,1), определить количество корней и экстремумов и найти их значение.

2. Решить систему уравнений:

3. Выполнить указанные операции с векторами и матрицами.

4. Использовать встроенные функции пакета для работы с файлами.

5. По данным эксперимента (или табличным данным) определить функциональную зависимость.

Построить матрицу входных данных, выбрать вид кривых (2 варианта) и определить коэффициенты функциональных зависимостей, которые описывают экспериментальные данные с ошибкой ±5%, построить графики исходных данных и функции.

Концентрация, X% КОН	10	20	30	35	40	45	50	55
Температурная депрессия, td°C	2,2	6	12,2	17	23,6	33	45	60,4

Выполнить проверку и анализ представления экспериментальных данных выбранными зависимостями (определить коэффициенты корреляции).

Задание выдано:

Приложение 3. Варианты расчетных заданий.

Таблица 1. Задание 1, 2.

Вар. 1 X = 0÷15	Вар. 2 X = 0÷10
Вар. 3 x = -5÷5 W(x) = x + 2·e(x·cos(x))	Вар. 4 x =-5÷5 Q(x) = x + 2·e(x·sin(x))
Вар. 5 x = 1÷5 Y(x) = 2 – (x –1)2+3·cos(3·x)	Вар. 6 x = 1,2÷7 G(x) = (cos(x)3+0,5)/(x+cos(x))
Вар. 7 x = 1÷10 M(x) = (4·x+7)(1/3)–3·cos(x) –4	Вар. 8 x = 1÷10 Q(x) = 1 – log(x)·sin(x)
Вар. 9 x = 1÷10 C(x) = 1 – sin(x)2·cos(x)2	Вар. 10 x = 0÷15 S(x) = xatan(x)·cos(x) – 7

Продолжение таблицы 1

Вар. 11 x = 0÷10 R(x) = 1 – atan(x)2·cos(x)	Вар. 12 x = 1÷10 K(x) = 2 – ln(x)2·sin(x)
Вар. 13 x = 1÷20 L(x) = 1 –log(x)cos(x)	Вар. 14 x = 1÷15 D(x) = (x+1)3·sin(x)2+x –10
Вар. 15 x = 10÷15 W(x) = (x –1)·cos(x) –5·esin(x)	Вар. 16 x = 1÷15 P(x) = sin(x)(x)–0,5·e4·cos(x)
Вар. 17 x = 1÷7 Y(x) = (x –1)3·sin(x)2–(x+1)2	Вар. 18 x = 1,2÷9 T(x) = sin(x)3/(x –2·cos(x)3)
Вар. 19 x = 1÷5 Y(x) = x2·sin2(x) –(x –1)3	Вар. 20 X = 1÷5 B(x) = x cos(x)· (x) –sin(x)

Продолжение таблицы 1

Вар. 21 x = 1÷8,5 Y(x) = x5·sin(x)2+x –20	Вар. 22 x = 0÷7 Z(x) = (sin(x)3+0,3) /xcos(x) +5
Вар. 23 x = 1÷9 T(x) = (sin(x)3 –0,6) /x2	Вар. 24 x = 0÷10 F(x) = 5cos(x) +5·sin(x)2 – 3
Вар. 25 x = 1÷10 C(x) = (sin(x)3 – 0.7) /x	Вар. 26 x = 1÷10,5 S(x) = (cos(x)3 – 0,2) /x
Вар. 27 x = 0÷7 Z(x) =(cos(x)3–0,5·x)/(xsin(x) +7)	Вар. 28 x = 1÷9 T(x) = sin(x)3/(x –2·cos(x)3)
Вар. 29 x = 1,2÷5,5 F(x) =(sin(x)3 –0,5)/(xsin(x)+7)	Вар. 30 x = 1÷7,2 G(x) = (cos(x)3+0,5)/(x+cos(x))

Таблица 2. Задание 3, 4.

Варианты зависимостей для вычисления элементов векторов и матриц.

Вар.	Зависимость	Вар.	Зависимость
1	Vk = 2·k/(k+1) Ms,k = 1/(s + k)	16	Vk = 2·k/(2·k+1) Ms,k = 2·s + 3·(s + k)
2	Vk = (2·k –1)·2·k Ms,k = 10·s + 2·k	17	Vk = 15/k+1,5 Ms,k = 2·s + 5·(k+1)
3	Vk = 1/(3·k-2) Ms,k = 10·s + 1/k	18	Vk = 2·k+1+2/k Ms,k = 2·(s + k)+0,5·k
4	Vk = 2·k/k Ms,k = k·2 + (s + k)·2	19	Vk = (2·k+5)·2·k+1 Ms,k = 10·s+1+3·k
5	Vk = 10/4·k Ms,k = 3·s + 2·k	20	Vk = 0,5+2·(k – 1,5) Ms,k = 5·s + 15·k
6	Vk = 10/k·2 Ms,k = 2·s + 5·(k+1)	21	Vk = 5/(3·k–3) Ms,k = 10·s+1+5/k
7	Vk = 0,5·k/2 Ms,k = 2·s + 10·k	22	Vk = 0,8·k/3 Ms,k = 3·s + 15·k
8	Vk = 10/k Ms,k = 0,5·s + 0,1·k	23	Vk = 20/k2+3 Ms,k = 1,5·s + 5,1·k
9	Vk = sin(k)/k Ms,k = (k +s ) ·05	24	Vk = sin(k)/3·(k+1) Ms,k = 2·(k +s )+ 2·s
10	Vk = cos(2·k)/k Ms,k = (1 + k)/(s +k)	25	Vk = cos(2·k)/2·(k -1,5) Ms,k = (5 + k)/(s +5)
11	Vk = cos(k)/k Ms,k = (k +s ) ·(1/3)	26	Vk = cos(k)/(k+0,1) Ms,k = (k +s ) ·(1/2)
12	Vk = (5·k+1)·2 Ms,k = 2·s –3·k	27	Vk = 5·(k+2)+3 Ms,k = 3·s –2·k
13	Vk = 20/(2+2·k) Ms,k = 3·s + (2+k)·3	28	Vk = 20/(5+3·k) Ms,k = 2·s+2·(1+k)
14	Vk = 2,5·k/k Ms,k = 10·s+(1+3·k)	29	Vk = 10/k Ms,k = 1,5·s + 5,1·k
15	Vk = sin(k)/k Ms,k = 2·(k +s ) +2·s	30	Vk = cos(2·k)/k Ms,k = (5 + k)/(s +5)

где значение s изменяется от 0 до 2, а значение к – от 0 до 4

Таблица 3. Задание 5.

Навчальне видання

Методичні вказівки до виконання розрахункових завдань (курсової роботи) з курсу «Інформатика» (Інженерні розрахунки у середах Excel та Mathcad) для студентів хімічних спеціальностей усіх форм навчання – Харків: НТУ „ХПІ”. 2012. – 24 с.

Укладачі: Коцаренко Віктор Олексійович

Іванов Віталій Анатолійович

Соловей Людмила Валентинівна

Роботу до друку рекомендував проф. В.І. Тошинський

Відповідальний за випуск проф.В.Є. Ведь

В авторській редакції

План 2011 р., п.

Підписано до друку 21.06.11 р. Формат 6084 1/16. Папір офісний.

Riso-друк. Гарнітура Таймс. Ум. друк. арк. 0,6. Облік. – вид.арк.0,7.

Наклад 100 прим. Зам № Ціна договірна.

__________________________________________________________________

Видавничий центр НТУ «ХПІ».

Свідоцтво про державну реєстрацію ДК №3657 від 24.12.2009 р.