3.5. Сетевая модель реализации решения

Планирование и управление комплексом работ по реализации решения представляет собой сложную и, как правило, противоречивую задачу. Оценка временных и стоимостных параметров, осуществляемая в рамках этой задачи, может быть произведена разными методами. Среди существующих хорошо зарекомендовал себя метод сетевого планирования и управления. Основой метода сетевого планирования является сетевой график (сетевая модель), представляющий собой информационно-динамическую модель, в которой отражаются взаимосвязи и результаты всех работ, необходимых для достижения конечной цели разработки.

Сетевая модель изображается в виде сетевого графика (сети), состоящего из стрелок и кружков. Стрелками в сети изображаются отдельные работы, а кружками - события. Над стрелками указывается ожидаемое время выполнения работ [4, 17].

Этапы разработки и управления ходом работ с помощью сетевого графика имеют следующую последовательность основных операций:

• составление перечня всех действий и промежуточных результатов (событий) при выполнении комплекса работ и графическое их отражение;

• оценка времени выполнения каждой работы;

• составление сетевого графика,

• расчёт основных параметров сетевого графика,

• определение критического пути,

• анализ сетевого графика и его оптимизация.

Определим события:

1. Сбор информации о фирмах разработчиках информационных систем.

2. Анализ информации собранной информации.

3. Выбор фирмы разработчика.

4. Заключение договора.

5. Совместное предпроектное обследование финансового управления.

6. Повышение квалификации персонала.

7. Выполнение фирмой разработчиком работ по созданию информационной системы (кодирование).

8. Установка необходимого оборудования.

9. Развертывание информационной системы в подразделениях финансового управления.

Для наступления каждого события необходимо выполнить соответствующие работы. Для этих работ необходимо определить продолжительность и количество трудовых ресурсов.

В таблице 3.2 представлены исходные данные для построения сетевой модели.

Таблица 3.2

Исходные данные для расчета параметров сетевого графика

Работа, непосредственно предшествующая данной (i-j)-й работе	Работа сетевого графика(i-j)	Трудоемкость (длительность) данной работы, дн.	Потребность в ресурсах для выполнения данной работы, чел.
-	1-2	3	3
-	1-3	5	3
-	1-6	1	3
1-2	2-3	1	4
1-2, 1-3, 2-3	3-4	1	3
1-2, 1-3, 2-3	3-5	3	3
1-2, 1-3, 2-3, 3-4	4-7	1	4
1-2, 1-3, 2-3, 3-5	5-7	3	2
1-2, 1-3, 2-3, 3-5	5-8	4	3
1-6	6-9	14	10
1-2, 1-3, 2-3, 3-4, 3-5, 4-7, 5-7	7-9	56	5
1-2, 1-3, 2-3, 3-5, 5-8	8-9	7	3

По исходным данным построим сетевую модель реализации выбранного варианта (рис. 3.1).

Проведем анализ сетевой модели с целью установления оптимальности плана. Для этого проведем подсчет показателей сетевого графика.

Раннее начало работы самое раннее время начала работы, определяется продолжительностью самого длинного пути от начального события до предшествующего события данной работы.

Рисунок 3.1 - Сетевой график выполнения работ

Раннее окончание работы - время окончания работы, если она начата в ранний срок.

Критический путь – самая продолжительная последовательность работ от исходного события до завершающего.

№ пути	Работы, лежащие на пути	Продолжительность, дни
TL1	1-2, 2-3, 3-4, 4-7, 7-9	62
TL2	1-2, 2-3, 3-5, 5-7, 7-9	66
TL3	1-2, 2-3, 3-5, 5-8, 8-9	18
TL4	1-6, 6-9	15
TL5	1-3, 3-4, 4-7, 7-9	63
TL6	1-3, 3-5, 5-7, 7-9	67 критич.
TL7	1-3, 3-5, 5-8, 8-9	19

Позднее окончание работы - самое позднее время окончания работы, которое не вызовет задержки всего комплекса работ, определяется разностью продолжительности критического пути и самого длинного пути от конечного события данной работы до завершающего события.

Позднее начало работы – самый поздний срок наступления окончания работы, из возможных, не срывающих сроков выполнения последующих работ.

Сопоставление ранних и поздних характеристик работ выявит запас времени. Если эти характеристики совпадают, то работы лежат на критическом пути и запасы времени у них отсутствуют.

Для остальных работ определяются запасы времени, представляющие собой разность поздних и ранних характеристик (начал и окончаний работ).

Общий резерв времени (Rij) - количество времени, на которое можно перенести начало работы или увеличить её продолжительность без изменения общего продолжительности процесса (разность позднего и раннего начала и/или разность позднего и раннего окончания).

Результаты расчетов временных параметров сетевого графика приведены в таблице 3.3.

Таблица 3.3

Результаты расчетов временных параметров сетевого графика

Работа	Временные параметры сетевого графика
ij	tij	tрнij	tроij	tпоij	tпнij	Rij
1-2	3	0	3	4	1	1
1-3	5	0	5	5	0	0
1-6	1	0	1	53	52	52
2-3	1	3	4	5	4	1
3-4	1	5	6	10	9	4
3-5	3	5	8	8	5	0
4-7	1	6	7	11	10	4
5-7	3	8	11	11	8	0
5-8	4	8	12	60	56	48
6-9	14	1	15	67	53	52
7-9	56	11	67	67	11	0
8-9	7	12	19	67	60	48
Длина критического пути: Tкр = 67 дней
Работы критического пути: 1-3, 3-5, 5-7, 7-9

Выполним краткий анализ сетевого графика.

Сетевой график содержит семь полных путей, один из которых критический. Критическим (наиболее продолжительным) является путь: 1-3, 3-5, 5-7, 7-9. Его продолжительность равна 67 дням (5+3+3+56). Задержка при выполнении любой работы на критическом пути (на рисунке выделен жирной линией) приведет к нарушению срока наступления соответствующего события критического пути, а следовательно, и к срыву всего комплекса работ. Остальные шесть полных путей короче критического и поэтому имеют некоторый резерв времени, например, путь 1-2, 2-3, 3-4, 4-7, 7-9 имеет резерв в 5 дней, путь 1-3, 3-5, 5-8, 8-9 имеет резерв в 48 дней.

Произведем оптимизацию выполнения комплекса работ с учетом ограничений по ресурсам.

Для оптимизации строится диаграмма (Рисунок 3.2), на которой совмещаются последовательные пути выполнения работ в соответствии с ранним началом событий и потребное количество людских ресурсов в каждый интервал времени (день).

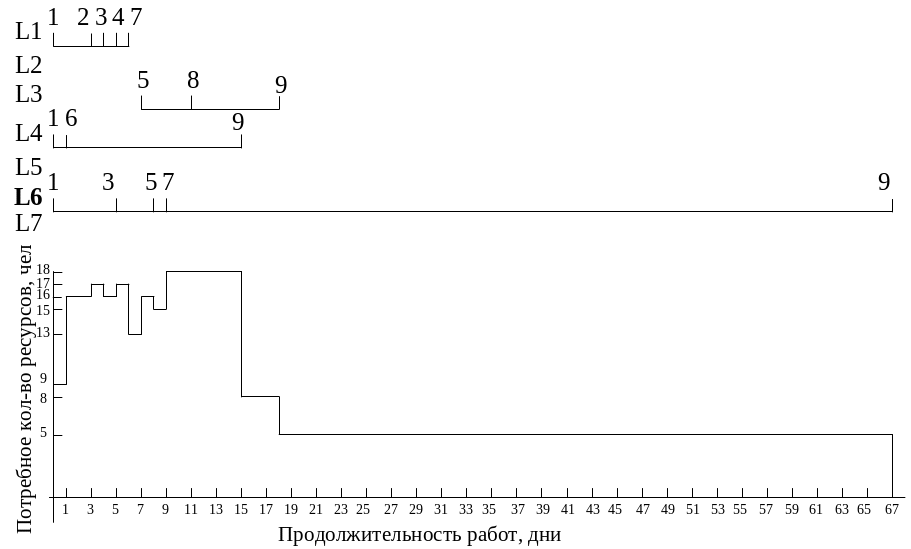
Рисунок 3.2 – Оптимизационная диаграмма

Например, в первый день количество потребных ресурсов составляет 9 человек (для выполнения работ 1-2 (3 чел.), 1-6 (3 чел.), 1-3 (3 чел)); во второй день потребно 16 человек (для выполнения работ 1-2 (3 чел.), 6-9 (10 чел.), 1-3 (3 чел) и т.д.

Оптимизацию графика проводить не требуется, так как наличное количество людских ресурсов - 20 человек превышает максимально необходимое потребное количество ресурсов.