10.4.2. Метод неполной взаимозаменяемости

Это метод, при котором требуемая точность замыкающего звена размерной цепи получается не при любых сочетаниях, а при ранее обусловленной части сочетаний размеров составляющих звеньев.

Сборка осуществляется без пригонки, регулировки и подбора звеньев.

Метод исходит из предположения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный характер, и вероятность того, что все звенья с самыми небла­гоприятными сочетаниями окажутся в одном изделии, весьма мала.

Такой метод расчета, который учитывает рассеяние размеров и вероятность их различных со­четаний, называется вероятностным методом расчета. Другими словами, метод допускает малый процент изделий, у которых замыкающее звено выйдет за рамки поля допусков. При этом расши­ряются допуски составляющих цепь размеров, и тем самым снижается себестоимость изготовле­ния деталей.

Задачей расчета является назначение допусков на составляющие звенья, соответствующих оди­наковой степени точности.

Учитывая случайный характер сочетаний действительных размеров деталей в изделии, восполь­зуемся уравнением для определения дисперсии суммы независимых случайных величин:

Допустим, что погрешность всех звеньев изменяется по закону нормального распределения, а границы рассеяния размеров для составляющих звеньев 6а совпадают с границами полей до­пусков, тогда:

Для замыкающего звена допустим, что:

где t — коэффициент риска. Тогда:

Обозначим через

(10.8)

Формула (10.8) устанавливает связь между допуском на замыкающий размер и допусками на со­ставляющие звенья.

Для того чтобы добиться одинаковой точности составляющих звеньев размерной цепи, восполь­зуемся известной формулой и подставим ее в выражение (10.8). Потребуем, чтобы к у всех звеньев были одинаковыми, тогда:

Окончательно получим:

(10.9)

Если предполагается, что рассеяние размеров близко, например, к закону Симпсона, то

При неизвестном характере рассеяния размеров рекомендуется принимать закон равной веро­ятности с

На основании предельных теорем теории вероятностей независимо от характера рассеяния размеров составляющих звеньев разброс размеров замыкающего звена размерной цепи будет близок к закону нормального распределения.

В зависимости от принятого процента риска Р значения t выбирают из ряда, приведенного в табл. 10.4.Приложение Д1.

Таблица 10.4

р, %	32.00	10.00	4.50	1.00	0.27	0.10	0.01
t	1.00	1.65	2.00	2.57	3.00	3.29	3.89

Пример

Вероятностный метод расчета рассмотрим на том же узле (см.рис.10). По техническим требо­ваниям необходимо обеспечить осевой зазор . Требуется назначить допуски и откло­нения на составляющие звенья при и нормальном законе распределения рассеяния размеров составляющих звеньев (процент брака и закон распределения студент выбирает сам).

Допуски и отклонения на ширину подшипниковых колец и монтажную высоту подшипников каче­ния, входящих в размерную цепь, назначать условно, как и на другие детали.

Решение

1. Определение номинальных размеров составляющих звеньев.

Этот пункт решения задачи полностью соответствует первому пункту при расчете на макси­мум — минимум.

2. Определение средней точности размерной цепи. Воспользуемся зависимостью (10.9):

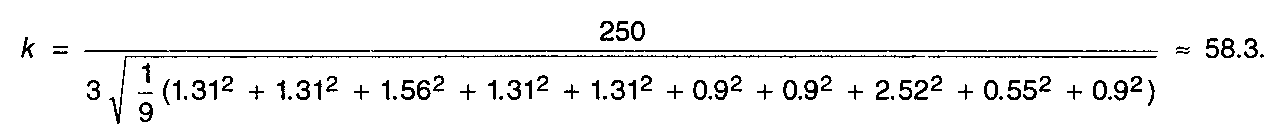
Найденное число единиц допуска лежит ближе к стандартному значению , что соот­ветствует 10-му квалитету. Допуски на все звенья назначаются по 10-му квалитету.

3. Определение истинного процента брака.

Из формулы (10.8):

что соответствует 0.693% брака (значения процента брака определяется по табл. П.7.1 прило­жения).

Полагаем, что такой процент брака нас устраивает. Если же количество брака мы сочли бы чрезмерным, тогда необходимо было допуски на ряд звеньев назначить по 9-му квалитету. Результаты поэтапных расчетов внесены в табл. 10.5.

Таблица 10.5

Обозна­чение звена	Номи­нальный размер, мм	, мкм	Обозна­чение основного отклонения	Квалитет	Допуск Т	Верхнее отклонение В	Нижнее отклонение Н	Середина поля допуска С
					мкм
	0.2	—	—	—	250	+250	0	+125
	19	1.31	h	10	84	0	-84	-42
	20	1.31	h	10	84	0	-84	-42
	42	1.56	h	10	100	0	-100	-50
	20	1.31	h	10	84	0	-84	-42
	19	1.31	h	10	84	0	-84	-42
	10	0.9		10	58	+29	-29	0
	8	0.9	h	10	58	0	-58	-29
	130	2.52	h	10	160	0	-160	-80
	2.2	0.55	—	10	40	+36	-4	+16
	10	0.9		10	58	+29	-29	0

4. Определение предельных отклонений звена .

Вначале определим координату середины поля допуска звена по формуле (10.5):