Амплитудно-импульсная модуляция

Дискретный модулирующий сигнал это чередующиеся посылки фиксированного уровня. Частным случаем дискретного модулирующего сигнала является цифровой сигнал, т.е. сигнал фиксированного уровня и фиксированной длительности. [ Баскаков].

Дискретный сигнал это, прежде всего, периодический сигнал, отвечающий следующему условию

Здесь Т – период повторения импульсов (рис.2.2).

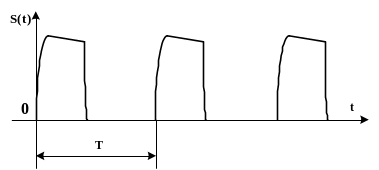
Периодическая импульсная последовательность

Известно, что любой периодический сигнал можно представить в виде бесконечного ряда синусоидальных колебаний с определенной амплитудой, начальной фазой и частотами кратными частоте повторения F₀=1/T

Этот ряд именуют рядом Фурье данного сигнала. Иная форма записи ряда Фурье с использованием ортогональных синусоидальных функций имеет вид

Коэффициенты S₀, а_n, b_n ряда Фурье рассчитываются по формулам

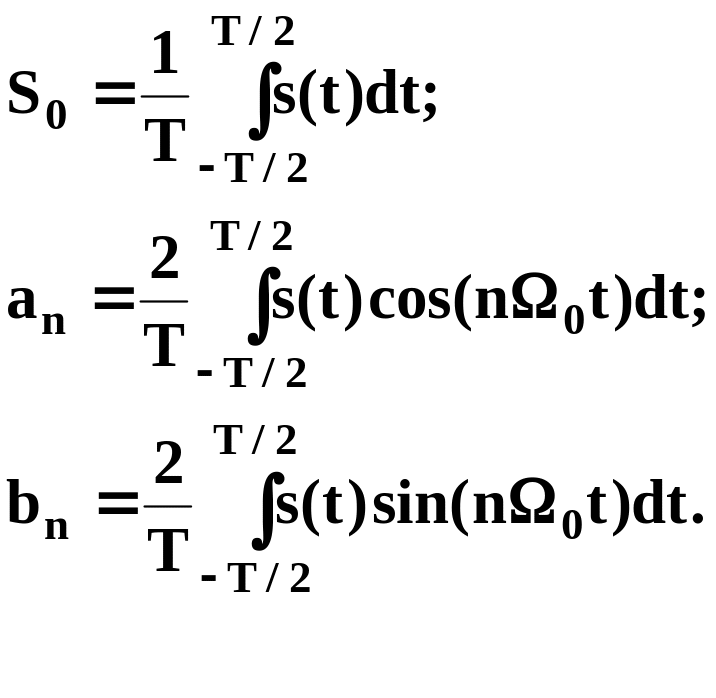
Строгое математическое описание импульсной последовательности по форме, близкой к прямоугольной, затруднительно. По этой причине при анализе передатчиков с импульсной модуляцией используется сигнал идеальной прямоугольной формы, математическое описание которого не вызывает затруднений.

Рассмотрим разложение в ряд Фурье периодическую импульсную последовательность прямоугольной формы.

Последовательность импульсов прямоугольной формы

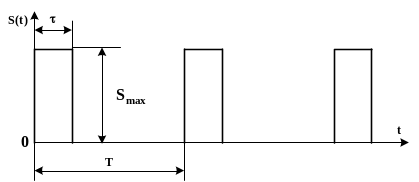
Ряд Фурье для периодической импульсной последовательности прямоугольной формы имеет вид

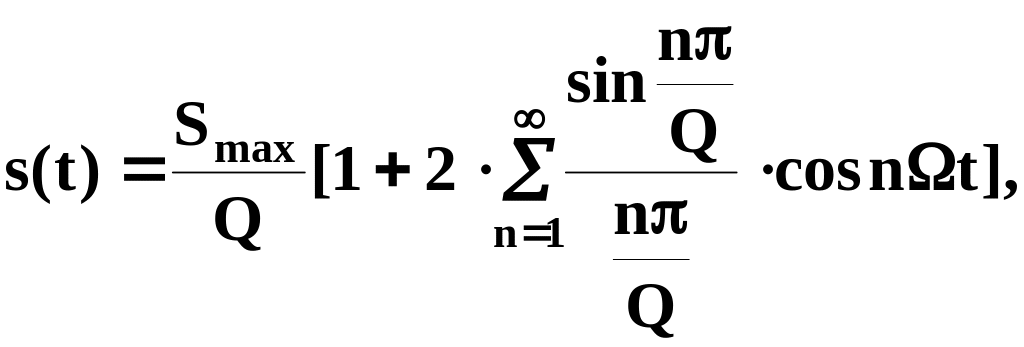где S_max – амплитуда импульсов, - скважность (величина обратная коэффициенту заполнения), - период повторения импульсов и их длительность соответственно.

На рис. представлены огибающие спектра прямоугольной импульсной последовательности при Q=3 и Q=10.

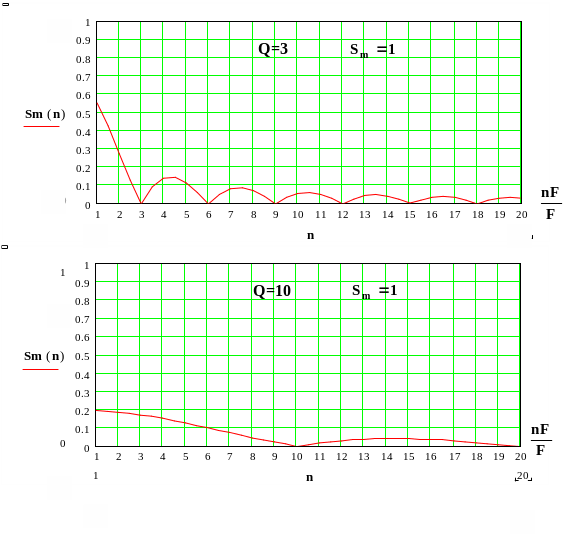
Как следует из формулы и видно из рисунков спектр частот прямоугольной импульсной последовательности линейчатый с бесконечным числом спектральных составляющих. Основная энергетическая нагрузка ложится на спектральные составляющие с частотами . Поэтому за полосу частот периодического сигнала прямоугольной формы принимают полосу, определяемую из соотношения

,

из которого следует, что полоса, занимаемая сигналом, тем шире, чем больше скважность (короче импульс) и чем больше частота повторения.

Если в качестве модулирующего сигнала использовать импульсную последовательность прямоугольной формы, то передатчике будет осуществляться импульсная модуляция по одному из параметров ВЧ сигнала: амплитуде, частоте или фазе. Каждая из перечисленных импульсных модуляций находит широкое применение в системах связи. Возможны также комбинированные виды импульсной модуляции, например, амплитуды и частоты в.ч. колебания. Из всего этого многообразия мы остановимся на наиболее простом виде – амплитудно импульсной модуляции (АИМ). В этом случае на выходе передатчика будет иметь место радиоимпульсы с амплитудой

.

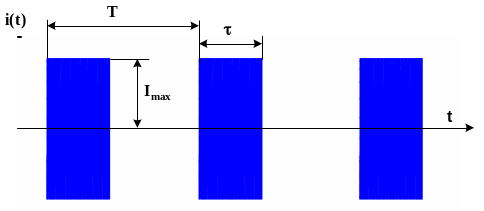
Радиоимпульсная последовательность

Математическое описание В.Ч. сигнала с АИМ имеет следующий вид

.

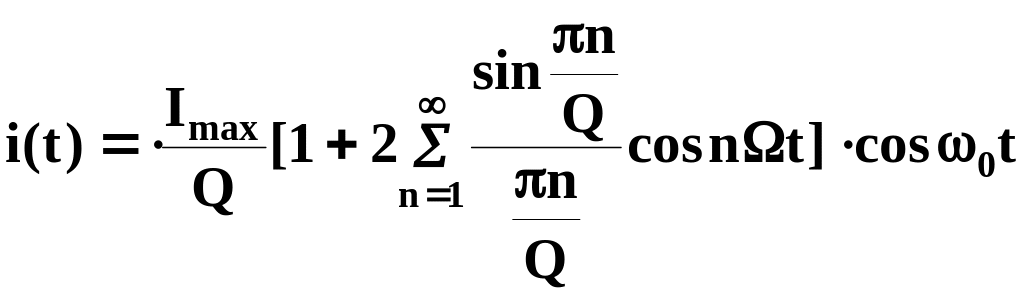Выполнив тригонометрическое преобразование заменой произведения косинусов на косинусы суммы и разности двух углов, получим выражение удобное для спектрального анализа

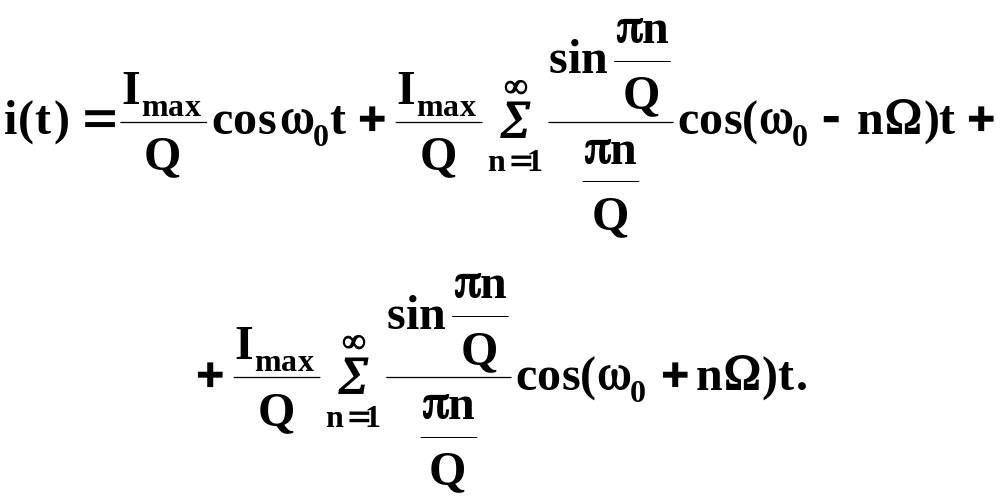
Спектр сигнала с АИМ показан на рисунке.

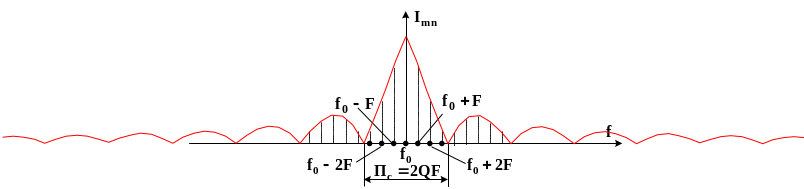
За полосу, занимаемую амплитудно импульсным сигналом, принимают

П_с= 2QF,

где F – частота следования радиоимпульсов, Q – скважность радиоимпульсной последовательности.