Угловая модуляция

Частотная и фазовая модуляции – это две разновидности угловой модуляции. Они имеют абсолютно одинаковый вид амплитудой модуляционной характеристики, но отличаются видом частотной модуляционной характеристики. При ЧМ ведущее значение имеет девиация частоты , которая обеспечивается частотным модулятором. Индекс модуляции является ведомой функцией и связан с девиацией частоты соотношением

При ФМ ведущее значение приобретает индекс модуляции , который обеспечивается фазовым модулятором. Девиация частоты является ведомой функцией и связана с индексом модуляции формулой

Частотные модуляционные характеристики для ведомых функций показаны на рисунке сплошными линиями

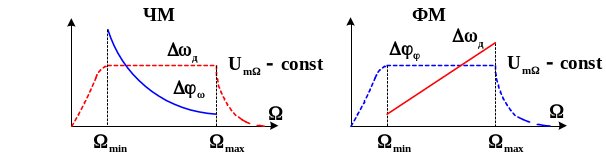
Математические соотношения и приведенные рисунки говорят о том, что фазовую модуляцию можно преобразовать в частотную, если модулирующий сигнал пропустить через блок частотных предъискажений, уменьшающий амплитуду модулирующего сигнала обратно пропорционально модулирующей частоте (примерно 6дБ на октаву)

,

а частотную модуляцию превратить в фазовую, если воспользоваться блоком частотных предъискажений, обеспечивающим рост амплитуды модулирующего сигнала пропорционально частоте модулирующего сигнала (примерно 6дБ на октаву)

.

Частотная модуляция полученная с помощью фазового модулятора и блока частотных предъискажений модулирующего сигнала получила название косвенного метода получения ЧМ.

Фазовая модуляция полученная с помощью частотного модулятора и блока частотных предъискажений модулирующего сигнала получила название косвенного метода получения ФМ.

Спектр сигнала с угловой модуляцией

Если убрать индексы при , то запись сигнала с ЧМ и ФМ неразличимы. Следовательно, спектр сигнала с ЧМ и ФМ будет иметь формально одинаковый вид. Выполним тригонометрические преобразования сигнала с УМ, положив для простоты

Известно, что выражения такого вида разлагаются в ряды с помощью функции Бесселя первого вида. Выполнив необходимые преобразования, получим следующее выражение

(1)

Широкополосная УМ.

Спектр сигнала с УМ при индексе модуляции .

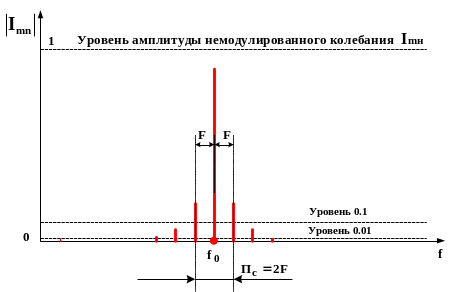
Оценка полосы, занимаемой сигналом с УМ, можно оценить либо по уровню 0.1 от амплитуды немодулированного колебания, либо по уровню 0.01 от амплитуды немодулированного колебания. В первом случае энергия всех составляющих спектра, которые превышают уровень 0.1, содержит 99% энергии всего сигнала. Полоса спектра сигнала при этом ограничении определяется соотношением

.

При ограничении по уровню 0.01 энергия всех составляющих спектра, которые превышают уровень 0.01, содержит 99.99% энергии всего сигнала. Полоса спектра сигнала при этом ограничении определяется формулой Манаева

.

В этой формуле индекс модуляции округляется до большего целого числа.

Угловая модуляция с индексом модуляции называется широкополосной, а с - узкополосной

Узкополосная УМ.

Спектр сигнала с УМ при индексе модуляции .

Спектральные составляющие верхней и нижней боковых частот при УМ различаются по фазе. Это видно из выражения (1). Поэтому информация без искажений может быть получена на приемной стороне только при наличии спектра нижней и верхней боковых полос. Использование одной полосы (верхней или нижней) для передачи информации при УМ не возможна.