Занятие 8. Сравнение бесконечно малых

Цель занятия:

отработать процедуру сравнения бесконечно малых.

Краткие теоретические сведения

1. Сравнение бесконечно малых функций:

Чтобы сравнить две функции и , являющиеся бесконечно малыми в окрестности одной и той же точки , нужно рассмотреть предел их отношения при :

;

по результату вычисления этого предела получаются следующие ответы:

1. если , то при , т.е. имеет более высокий порядок малости, чем б.м. , при ;

2. если , то при , т.е. имеет более высокий порядок малости, чем , или имеет более низкий порядок малости по сравнению с при ;

3. если А – это число , то при , т.е. и имеют одинаковый порядок малости при ;

в частности, если А=1, то при , т.е. и эквивалентны при ;

4. если предел А не существует, то б.м. и сравнить нельзя.

Таким образом, для решения задачи «сравнить две бесконечно малые функции» нужно вычислять предел отношения этих функций при , где – это та точка, в которой обе сравниваемые функции являются бесконечно малыми.

2. Порядок малости одной бесконечно малой функции относительно другой:

Число р называется порядком б.м. относительно б.м. при , если при , т.е. если и имеют одинаковый порядок малости при .

Из этого определения следует, что число p определяется из следующего условия:

, где - число, .

Аудиторные задания

Задача 1

Сравните две бесконечно малые величины:

1) и при ;

2) и при ;

3) и при ;

4) и при ;

5) и при ;

6) и при ;

Ответы:

1) ; 2) ; 3) ;

4) ; 5) ; 6) .

Задача 2

Определите порядок малости p относительно x функции f(x), которая является бесконечно малой при :

1) ; 2) ; 3) ; 4) ; 5) .

Ответы: 1) p=2; 2) p=1/2; 3) p=1/2; 4) p=3/2; 5) p=1.

Задания для домашнего выполнения

Задача 1

Сравните две бесконечно малые величины:

1) и при ;

2) и при ;

3) и при ;

4) и при ;

5) и при ;

Задача 2

Определите порядок малости p относительно x функции f(x), которая является бесконечно малой при :

1) ; 2) ; 3) ; 4) ; 5) .

Ответы к заданиям для домашнего выполнения

Задача 1

1) ; 2) ; 3) ;

4) ; 5) .

Задача 2

1) p=1; 2) p=10; 3) p=1; 4) p=1; 5) p=2.

Занятие 9. Исследование функций на непрерывность

Цель занятия:

1. отработать основные определения, связанные с непрерывностью функции в точке;

2. научиться описывать по графику свойство непрерывности функций.

Краткая теоретическая справка

1. Определение непрерывности функции в точке:

Функция называется непрерывной в точке x₀, если выполняются следующие условия:

1. точка 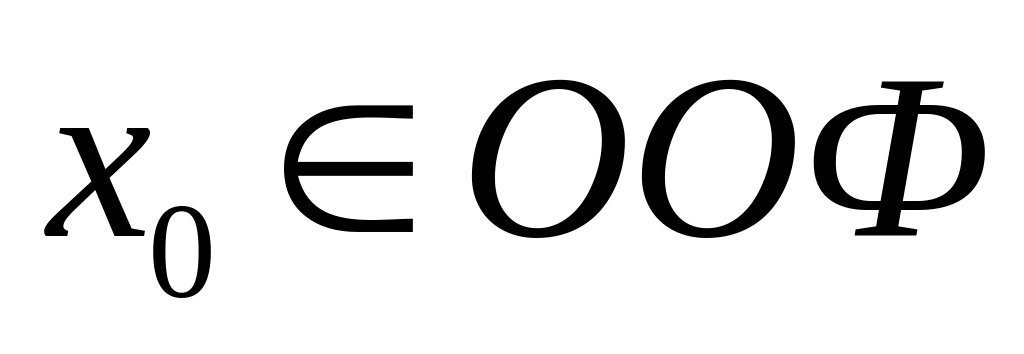вместе с некоторой своей окрестностью;

2. конечный ;

3. , т.е. этот предел совпадает со значением функции в точке .

Если функция непрерывна в точке , то это означает, что её график проходит через точку , не прерываясь.