1. Определение предела функции при на языке последовательностей (по Гейне):

2. Определение предела функции при на языке окрестностей (по Коши):

3. Определения предела функции на языке « »:

1)

т.е. , означает, что значения функции становятся сколь угодно близкими к числу А, если брать значения аргумента x достаточно близкими к числу a;

2)

т.е. означает, что значения функции становятся сколь угодно большими по модулю, если брать значения аргумента x достаточно близкими к числу a;

3)

т.е. означает, что значения функции становятся сколь угодно близкими к числу A, если брать значения аргумента x достаточно большими по модулю;

4)

т.е. , означает, что значения функции становятся сколь угодно большими по модулю, если брать значения аргумента x также достаточно большими по модулю.

4. Определение бесконечно малой (б.М.), бесконечно большой (б.Б.) и локально ограниченной (лок.Огр.) функции при и некоторые связи между этими понятиями:

1. – б.м. при

2. – б.б. при

3. – лок.огр. при в которой множество значений функции является ограниченным;

4. если конечный то функция является локально ограниченной при

5. если , то функция является бесконечно большой при

6. существование конечного предела функции при равносильно представлению этой функции в виде суммы этого предела и бесконечно малой функции при :

где – это б.м. функция при

5. Односторонние пределы и их связь с пределом функции:

1. левосторонний предел:

правосторонний предел:

2. 

3. 

Аудиторные задания

Задача 1

Используя определение предела функции на языке докажите что:

1) ; 2) ; 3) ;

4) ; 5) ; 6) .

Задача 2

По графику функции дайте ответы на вопросы о предельном поведении функции в окрестностях различных значений её аргумента:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. укажите точки в окрестностях которых функция является бесконечно малой;

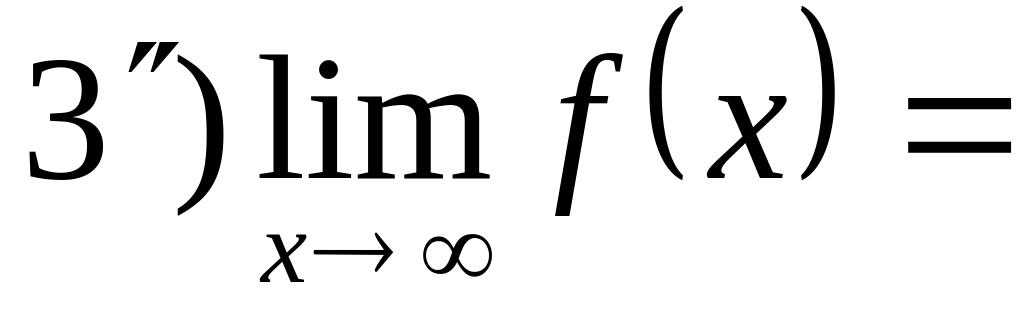
9. укажите точки в окрестностях которых функция является бесконечно большой;

10. укажите точки, в окрестностях которых функция является локально ограниченной.

Задача 3

Представьте функцию , имеющую конечный предел в каждой из точек , в виде суммы этого предела и функции , бесконечно малой при :

1)

2)

3)

Ответы:

1) если , то , где , - б.м. при ;

если , то , где , - б.м. при ;

2) если , то , где , - б.м. при ;

если , то , где , - б.м. при ;

3) если , то , где , - б.м. при ;

если , то , где , - б.м. при ;

если , то , где , - б.м. при .

Задания для домашнего выполнения

Задача 1

Используя определение предела функции на языке , докажите что:

1) ; 2) ; 3) ; 4)

Задача 2

По графику функции ответить на вопросы о предельном поведении функции в окрестностях различных значений её аргумента:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. укажите точки в окрестностях которых функция является бесконечно малой;

9. укажите точки в окрестностях которых функция является бесконечно большой.

10. укажите точки, в окрестностях которых функция является локально ограниченной.

Задача 3

Представьте функцию , имеющую конечный предел в каждой из точек , в виде суммы этого предела и функции , бесконечно малой при :

1)

2)

3) .

Ответы к заданиям для домашнего выполнения

Задача 3

1) если , то , где , - б.м. при ;

если , то , где , - б.м. при ;

если , то , где , - б.м. при ;

2) если , то , где , - б.м. при ;

если , то , где , - б.м. при ;

3) если , то , где , - б.м. при ;

если , то , где , - б.м. при .

Занятие 5. Теоремы о функциях, имеющих конечные пределы, о бесконечно малых, бесконечно больших и локально ограниченных функциях. Раскрытие основных неопределенностей, образованных алгебраическими функциями

Цель занятия:

1) использовать теоремы о конечных пределах функций, о бесконечно малых, бесконечно больших и локально ограниченных функциях для практического вычисления пределов;

2) рассмотреть приемы раскрытия неопределенностей , , , образованных алгебраическими функциями.

Краткие теоретические сведения