74

Тема 1. Предел и непрерывность функций одной переменной

Всего 10 занятий.

Занятие 1. Определение предела числовой последовательности; сходящиеся и

расходящиеся последовательности; бесконечно малые, бесконечно большие и

ограниченные последовательности. Признаки существования пределов.

Занятие 2. Вычисление пределов последовательностей с помощью свойств

сходящихся, бесконечно малых, бесконечно больших и ограниченных

последовательностей.

Занятие 3 . Самостоятельная работа №1 «Последовательности и их пределы».

Занятие 4. Определения предела функции в точке , и при .

Бесконечно малые, бесконечно большие и локально ограниченные функции.

Чтение предельного поведения функции по её графику.

Занятие 5. Теоремы о функциях, имеющих конечные пределы, о бесконечно малых, бесконечно больших и локально ограниченных функциях. Раскрытие основных неопределенностей, образованных алгебраическими функциями.

Занятие 6. Основные правила раскрытия неопределенностей. Замечательные пределы. Раскрытие неопределенностей с помощью замены эквивалентных бесконечно малых.

Занятие 7. Самостоятельная работа № 2 «Пределы функций».

Занятие 8. Сравнение бесконечно малых.

Занятие 9. Исследование функций на непрерывность.

Занятие 10. Контрольная работа.

Цели работы по теме:

1. усвоить основные понятия, связанные с предельным поведением изменяющихся величин (независимых переменных, последовательностей, функций одного аргумента) – на уровнях определений и чтения по графикам;

2. отработать практические приемы вычисления пределов и раскрытия основных неопределенностей;

3. сформировать навыки качественного описания и графического иллюстрирования предельного поведения функций;

4. усвоить основные определения в сравнении бесконечно малых функций, непрерывности функций, точек разрыва;

5. уметь исследовать функцию на непрерывность в точке и описывать непрерывность функции по её графику.

Занятие 1. Определение предела числовой последовательности; сходящиеся и расходящиеся последовательности; бесконечно малые, бесконечно большие, ограниченные и монотонные последовательности. Признаки существования предела последовательности

Цель занятия:

отработать основные определения, связанные с пределом числовой последовательности.

Краткие теоретические сведения

1. Определение числовой последовательности:

Числовой последовательностью называется отображение множества натуральных чисел на некоторое числовое множество :

.

2. Определение конечного предела последовательности:

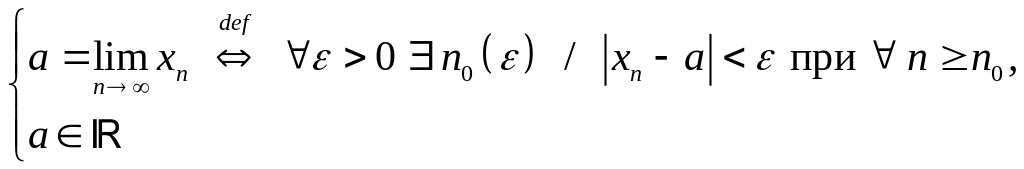
т.е. если то это означает, что для достаточно больших номеров n члены последовательности становятся сколь угодно близкими к числу a.

3. Определение бесконечного предела последовательности:

если переобозначить где – это большое число, то последнее определение можно сформулировать так:

т.е. если то это означает, что для достаточно больших номеров n члены последовательности становятся по модулю сколь угодно большими.

4. Определение сходящейся и расходящейся последовательности:

называется

5. Определение бесконечно малой, бесконечно большой , ограниченной и монотонной последовательности:

послед. называется бесконечно малой, если

послед. называется бесконечно большой, если

послед. называется ограниченной, если её члены образуют ограниченное множество, т.е. числа A и B, такие что при

;

послед. называется монотонно возрастающей, если ;

послед. называется монотонно убывающей, если .

6. Признак существования конечного предела последовательности

Для того, чтобы последовательность имела конечный предел a, необходимо и достаточно, чтобы эта последовательность представлялась как сумма числа a и бесконечно малой последовательности:

6. Теорема Вейерштрасса о пределе монотонной последовательности

Аудиторные задания

Задача 1

Среди данных последовательностей укажите номера последовательностей:

а) сходящихся, б) расходящихся, в) бесконечно малых, г) бесконечно больших,

д) ограниченных, е) монотонных:

1) 2) ; 3) ;

4) ; 5) ; 6) ; 7) ;

8) 9) 10)

Ответ: а) сходящиеся последовательности: 1), 2), 8), 9), 10);

б) расходящиеся последовательности: 3), 4), 5), 6), 7);

в) бесконечно малые последовательности: 1), 2), 8), 9);

г) бесконечно большие последовательности: 3), 5), 7);

д) ограниченные последовательности: 1), 2), 6), 8), 9), 10);

е) монотонные последовательности: 1), 5), 7), 8), 10).

Задача 2

Используя определение предела последовательности докажите, что

1)

2)

3) является бесконечно малой, если ;

4) является бесконечно большой, если .

Задача 3

Используя признак существования конечного предела последовательности, докажите, что

1) 2) 3) 4)

Задача 4

Используя теорему Вейерштрасса, докажите, что следующие последовательности являются сходящимися:

1) ;

2) .

Задания для домашнего выполнения

Задача 1

Среди данных последовательностей укажите номера последовательностей:

а) сходящихся, б) расходящихся, в) бесконечно малых, г) бесконечно больших,

д) ограниченных, е) монотонных:

1) 2)   3)  ; 4)

5) 6) ;            7) ;        8) ;

9) ; 10) .

Задача 2

Используя определение предела последовательности докажите, что

1) является бесконечно большой, если ;

2) является бесконечно малой, если ;

3) , если

4) , если ;

5) если ;

6) если .

Задача 3

Используя признак существования конечного предела последовательности, докажите, что:

1) ; 2) ;   3)   .

Задача 4

Используя теорему Вейерштрасса, докажите, что следующие последовательности являются сходящимися:

1)

2) ;

Ответы к задачам для домашнего выполнения

Задача 1

а) сходящиеся последовательности: 1), 3), 5), 6), 8), 10);

б) расходящиеся последовательности: 2), 4), 7), 9);

в) бесконечно малые последовательности: 1), 6), 8), 10);

г) бесконечно большие последовательности: 2);

д) ограниченные последовательности: 1), 3), 4), 5), 6), 7), 8), 10);

е) монотонные последовательности: 3), 6), 8).

Задача 4

1)

конечный - сходящаяся последовательность;

2)

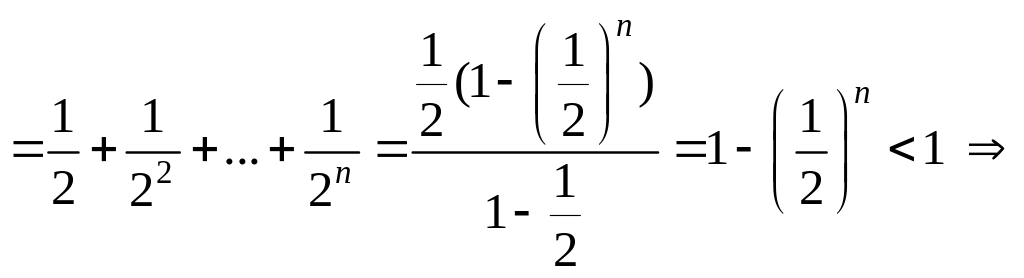
конечный сходится.