1.3.2 Влияние напряжений на перераспределение вакансий при ионном облучении

Результаты экспериментов по ионному облучению свидетельствуют, что эволюция дефектов является существенно неравновесным процессом [11, 16-26]. Поскольку характерное время формирования дефектной структуры оказывается существенно меньшим, чем время распространения дефектов за счет диффузии, для описания эффекта “дальнодействия” необходимы методы неравновесной термодинамики, учитывающей отсутствие локального равновесия [13]. Облученный материал, в общем случае, обладает сложной дефектной структурой, эволюционирующей во времени и не поддающейся прямому наблюдению в процессе эволюции. Тем не менее, анализ экспериментальной ситуации показывает, что эффект “дальнодействия” наиболее ярко проявляется тогда когда исходный материал насыщен дефектами (в частности, вакансиями и дислокациями), причем распространение вакансий может играть основополагающее значение.

При моделировании влияния напряжений на перераспределение вакансий при ионном облучении рассматривается процесс облучения пластины, толщина которой d<<L, где L – характерный поперечный размер пластины (Рис. 8). Верхний слой толщиной W(E), определяется энергией имплантируемых атомов (область каскадного перемешивания), представляет собой частично разрушенную решетку, насыщенную межузельными атомами, вакансиями, атомами примеси и прочими дефектами.

Рис. 8. Схематичное изображение облучаемой пластины.

При ионной имплантации в результате торможения ионов генерируются упругие волны. Они могут воздействовать на примесно-дефектные атмосферы протяженных дефектов и способствовать их модификации на больших расстояниях от поверхности пластины. Если ограничиться предположением, что облучаемая пластина – бездислокационный монокристалл, то в такой ситуации релаксация облученной системы к положению равновесия будет полностью определяться динамикой точечных дефектов. Соответственно напряженное состояние системы в каждый момент времени является стационарным и определяется мгновенным распределением дефектов.

1.3.4 Эволюции кластеров радиационных дефектов при ионном облучении твердых тел

В работе [15] проведен анализ эволюции концентрации точечных дефектов при ионном облучении твердых тел. Предложена приближенная аналитическая методика для ее описания с учетом диффузии и некоторых вторичных процессов (рекомбинация точечных дефектов и образование дивакансий). Рассмотрена среда, в которой образовывается кластер точечных радиационных дефектов (вакансий имеждоузельных атомов) с эллипсоидальной симметрией и гауссовым распределением концентрации после попадания в нее быстрой частицы (электрона, иона). Дефекты диффундируют с постоянным коэффициентом диффузии и участвуют в образовании дивакансий (по бимолекулярному механизму). Одновременно происходит прямая рекомбинация дефектов друг с другом. В работе определялись концентрации междоузельных атомов, вакансий и дивакансий, как функции координат и времени, при наложении (в пространстве и времени) на кластер дефектов, сформированный одной радиационной частицей (ионом), кластеров, созданных другими частицами (ионами), в зависимости от дозы и плотности ионного тока.

В результате попадания одной частицы образуется кластер дефектов [15]. Предполагается, что междоузельные атомы имеют существенно больший коэффициент диффузии и покидают поврежденную область образца быстрее вакансий. Распределение концентрации междоузельных атомов I(r,,z,t) и вакансий V(r,,z,t) по радиальной (r), угловой () и осевой (z) координатам в момент окончания динамической стадии эволюции каскада, принятый за начало отсчета по времени t=0 имеет вид:

где – функция ошибок [2].

Динамика точечных радиационных дефектов на этапе стабилизации кластеров может быть описана с учетом их диффузии, а также их рекомбинации друг с другом и образования дивакансий [15]. В цилиндрической системе координат можно записать:

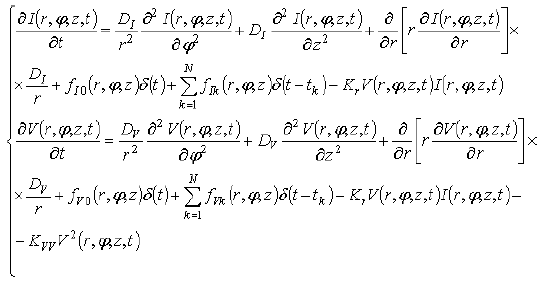
Данная система описывающим перераспределение дивакансий уравнением:

где (r,,z,t) и D_ – соответственно концентрация и коэффициент диффузии дивакансий, – кинетический коэффициент распада дивакансий,

В работе [15] определялись концентрации междоузельных атомов, вакансий и дивакансий, как функции координат и времени, при наложении (в пространстве и времени) на кластер дефектов, сформированный одной радиационной частицей (ионом), кластеров, созданных другими частицами (ионами), в зависимости от дозы и плотности ионного тока. Расчеты произведены приближенно помощью метода усреднения функциональных поправок с учетом дискретного во времени и пространстве попадания ионов на поверхность образца.