14.3. Расчет эффективной ставки сложных процентов при выдаче ссуды по сложной процентной ставке

Пусть i – сложная процентная ставка, п – период начисления, i_э – эффективная ставка сложных процентов. Банк выдает ссуду на срок п по ставке i, удерживает с нее долю комиссионных h и хочет выяснить доходность этой операции. Наращенные суммы равны:

P(1 + i)ⁿ = (P – hP)(1 + i_э)ⁿ

Отсюда (1 + i)ⁿ = (1 – P)(1 + i_э)ⁿ → i_э = .

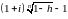Пример 68. При выдаче кредита на n = 3 года по сложной процентной ставке i = 12% годовых удерживаются комиссионные h = 1% суммы ссуды. Определим доходность этой операции в виде эффективной ставки сложных процентов.

Доходность операции равна:

i_э = = (1 + 0,12) 0,124 (= 12,4% годовых).

Задача 68. При выдаче кредита на n = 2 года по сложной процентной ставке i = 14% годовых удерживаются комиссионные h = 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки сложных процентов.

Замечание. Аналогично вышесказанному разбираются и другие возможные случаи.

9