13.4. Случай сложной процентной ставки

Пусть Р – первоначальная сумма, п – период начисления, i – сложная процентная ставка, q – ставка налога на проценты.

Метод взыскания налога (сумма налога на проценты определяется сразу за весь период начисления или каждый год отдельно) в случае сложной процентной ставки не влияет на общую сумму налога. Но для плательщика налога вовсе не безразлично, когда он его платит.

Наращенная сумма без учета налога S = P(1 + i)ⁿ, а проценты I = P(1 + i)ⁿ – P.

Поэтому величина налога на проценты qI= q(P(1 + i)ⁿ – Р).

Отсюда наращенная сумма с учетом налога

S = P(1 + i)ⁿ – qI = P(1 + i)ⁿ – q(P(1 + i)ⁿ – P) = P((1 – q)(1 + i)ⁿ + q).

Пример 65. Первоначальная сумма Р= 5000 руб., период начисления п = 3 года, сложная процентная ставка i = 15% годовых, ставка налога на проценты q = 12%.

Тогда наращенная сумма

S = P((1 – q)(1 + i)ⁿ + q).= 5000×((1 – 0,12)(1 + 0,15)³ + 0,12) = 7291,85 руб.

Задача 65. Первоначальная сумма Р= 7000 руб., период начисления п = 2 года, сложная процентная ставка i = 14% годовых, ставка налога на проценты q = 13%. Найти наращенную сумму.

Замечание. Аналогичные рассуждения о реальной ставке доходности с учетом налога можно провести и для случаев номинальной ставки сложных процентов и непрерывного начисления процентов.

Глава 14. Доходность удержания комиссионных

Рассмотрим несколько случаев расчета доходности при удержании банком комиссионных.

Пусть h – доля комиссионных в размере ссуды, то есть первоначальная сумма Р уменьшается на величину hР.

14.1. Расчет эффективной ставки простых процентов при выдаче ссуды по простой процентной ставке

Пусть i – простая процентная ставка, п – период начисления, i_э – эффективная ставка простых процентов. Банк выдает ссуду на срок п по ставке i, удерживает с нее долю комиссионных h и хочет выяснить доходность i_э этой операции.

Наращенные суммы равны: P(1 + ni) = (Р – hP)(1 + ni_э). Отсюда

1 + ni = (1 – h)(1 + ni_э) →

Если срок п выражен в днях, то в последнюю формулу нужно подставить п = t/K, где t – срок (в днях), K – продолжительность года:

Пример 66. При выдаче кредита на п = 0,5 года по простой процентной ставке i = 12% годовых удерживаются комиссионные h = 1% суммы ссуды. Определим доходность этой операции в виде эффективной ставки простых процентов.

Доходность операции равна:

0,1414 (= 14,14% годовых).

Мы видим, что доходность операции по выдаче ссуды с удержанием комиссионных выше, так как сумма выданной ссуды уменьшается.

Задача 66. При выдаче кредита на п = 0,25 года по простой процентной ставке i = 14% годовых удерживаются комиссионные h = 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки простых процентов.

14.2. Расчет эффективной ставки сложных процентов при выдаче ссуды по простои процентной ставке

Пусть i – простая процентная ставка, п – период начисления, i_э – эффективная ставка сложных процентов. Банк выдает ссуду на срок п по ставке i, удерживает с нее долю комиссионных h и хочет выяснить доходность этой операции. Наращенные суммы равны:

P(1+ni) = (P – hP)(1 + i_э).

Отсюда 1+ni = (1 – h)(1 + i_э) → i_э = .

Пример 67. При выдаче кредита на п = 3 года по простой процентной ставке i = 20% годовых удерживаются комиссионные h = 1% суммы ссуды. Определим доходность этой операции в виде эффективной ставки сложных процентов.

Доходность операции равна:

i_э = 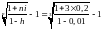≈ 0,174 (= 17,4% годовых).

Задача 67. При выдаче кредита на п = 2 года по простой процентной ставке i = 18% годовых удерживаются комиссионные h = 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки сложных процентов.