3. Пример расчёта фнч

Требуется рассчитать ФНЧ Баттерворта с граничной частотой полосы пропускания 1000 Гц и граничной частотой полосы задерживания 3125 Гц, с максимальным затуханием в полосе пропускания 0,08 дБ и гарантированным затуханием в полосе задерживания 71,6 дБ, двусторонне нагруженного на сопротивления 600 Ом.

В принятых обозначениях технические требования к фильтру имеют вид: ФНЧ Баттерворта с = 0,08 дБ на fc = 1000 Гц, = 71,6 дБ на fs = 3125 Гц, R1 = R2 = 600 Ом.

1. Определяем требуемый порядок ФНЧ Баттерворта в соответствии с выражением (2)

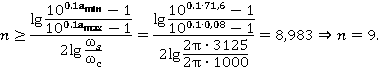
2. Определяем значение нормированной частоты среза .

Известно, что табулированный нормированный ФНЧ Баттерворта на имеет затухание . Для определения такой , на которой ФНЧ Баттерворта имеет затухание , воспользуемся выражением (1), присвоив переменным следующие значения: = 3 дБ на = 1, = 0,08 дБ на :

Решая полученное уравнение относительно , получим:

3. Выбираем принципиальную схему ФНЧ Баттерворта. Так как поря­док фильтра n= 9 - нечётный, то остановимся на варианте А схемы (рисунок 4), содержащем меньшее количество индуктивностей. Выбранная принципиальная схема представлена на рис.6.

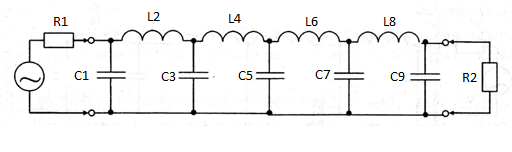
Рис 6. Принципиальная схема ФНЧ Баттерворта 9-го порядка

4. Определяем параметры нормированного ФНЧ Баттерворта 9-го по­рядка по таблице значений элементов фильтров Баттерворта (табл. П.1):

5. Определяем частотный масштабный множитель в соответствии с выражением (6):

и коэффициент масштабирования импедансов в соответствии с (9)

6. Масштабируем (денормируем) та6улированный нормированный ФНЧ-прототип Баттерворта по частоте и импедансу, используя выражения (10), (11),(12):

Корректировать полученные значения емкостей конденсаторов под промышленные номиналы в данном примере не представляется возможным ввиду относительно большого их количества при порядке n=9.

7. Построение и анализ АЧХ и ФЧХ полученного ФНЧ Баттерворта.

Составим эквивалентную расчётную схему, заменив в принципиальной схеме (рис.4) фильтр каскадным соединением трёх, эквивалентных П- и Т- образным звеньям фильтра, четырехполюсников N1,N2 и N3. Полученная эквивалентная схема представлена на рис.7.

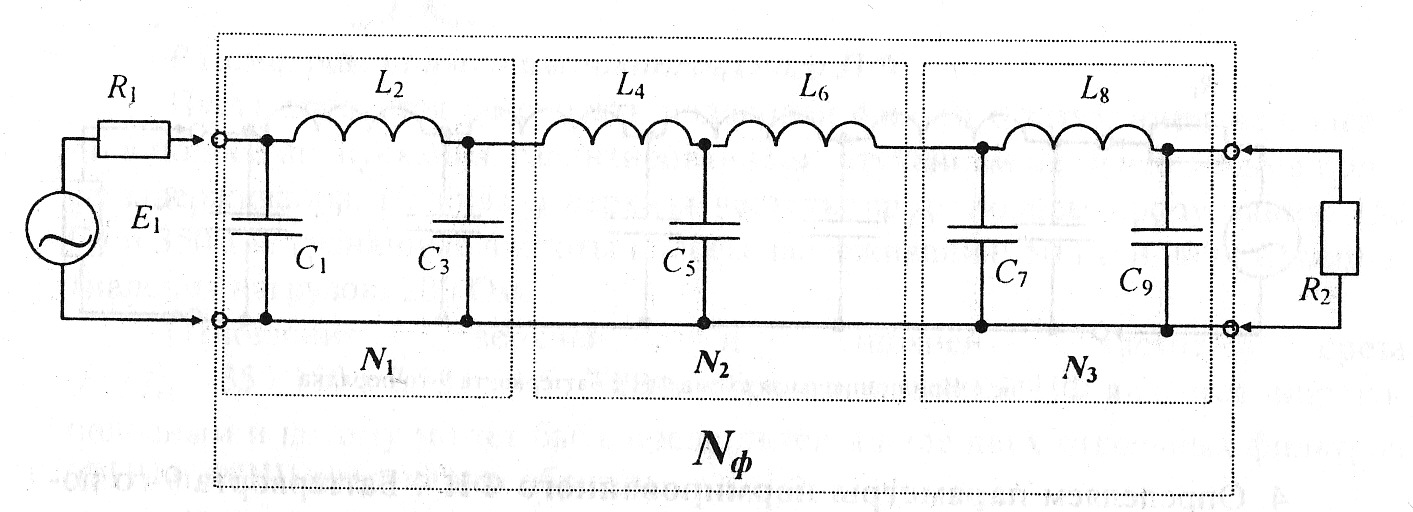
Рисунок 7. Эквивалентная расчётная схема замещения ФНЧ Баттерворта 9-го порядка

Коэффициенты A,В,С,D эквивалентного четырёхполюсника фильт­ра могут быть получены перемножением матриц А, В, С, D-коэффициентов четырехполюсников звеньев:

.

Выразим А, В, С, D-коэффициенты четырёхполюсников через параметры элементов соответствующих звеньев фильтра.

В полученных выражениях полные сопротивления и проводимости соответствующих элементов фильтра:

Комплексная рабочая передаточная функция фильтра

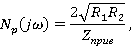
где полное приведённое (к ) сопротив­ление передачи фильтра.

Из комплексной передаточной функции выражается АЧХ фильтра, ее построение и сравнение с заданными параметрами.

4. Исходные данные

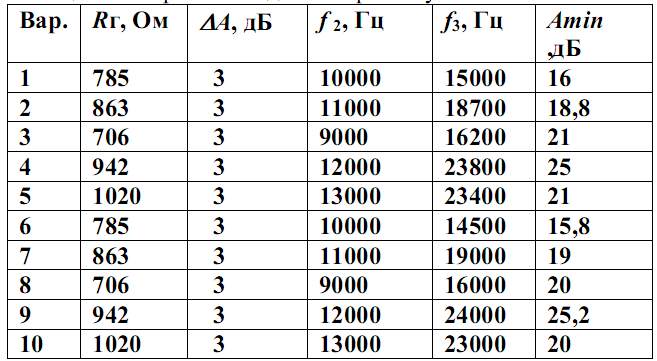
Исходные данные для расчета ФНЧ Баттерворта приведены в таблице 6.1, для ФНЧ Чебышева в таблице 6.2.

Таблица 6.1 Варианты заданий к расчету ФНЧ Баттерворта

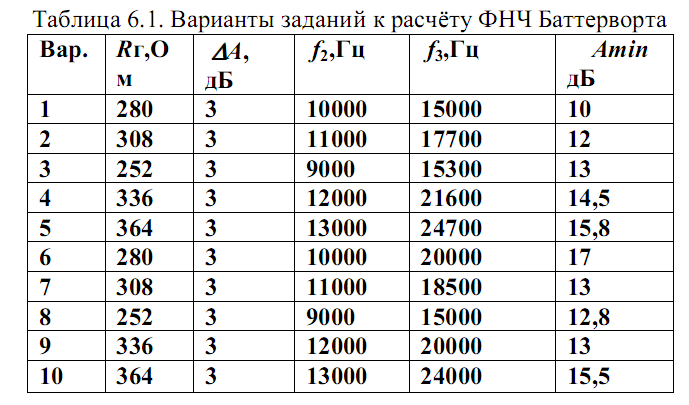
Таблица 6.2 Варианты заданий к расчету ФНЧ Чебышева

ПРИЛОЖЕНИЕ 1

Значения элементов фильтров-прототипов

Эти таблицы предназначены для фильтров, имеющих одинаковые сопро­тивления нагрузки на входе и выходе. Все данные таблиц нормированы для частоты среза полосы пропускания

1 рад/с и входного и выходного сопротив­лений 1 Ом. На частоте среза затухание равно: у фильтров Баттерворта 3 дБ, у фильтров Чебышева - размаху пульсаций в полосе пропускания (дБ). В таб­лицах значения элементов даны таким образом, что верхняя схема соответст­вует обозначениям элементов в верхней части таблицы, а нижняя схема - обо­значения внизу таблицы.

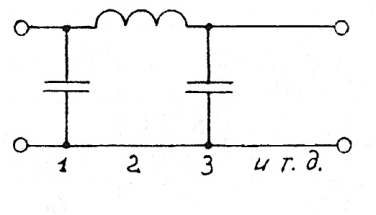
Таблица П. 1.1

Значения элементов фильтров Баттерворта 2-9-го порядков

п	C1	L2	C3	L4	C5	L6	С7	L8	С9
2	1,414	1,414
3	1,000	2,000	1,000
4	0,7654	1,848	1,848	0,7654
5	0,6180	1,618	2,000	1,618	0,6180
6	0,5176	1,414	1,932	1,932	1,414	0,5176
7	0,4450	1,247	1,802	2,000	1,802	1,247	0,4450
8	0,3902	1,111	1,663	1,962	1,962	1,663	1,111	0,3902
9	0,3473	1,000	1,532	1,879	2,000	1,879	1,532	1,000	0,3473
n	L1	С2	L3	C4	L5	С6	L7	C8	L9

Таблица П. 1.2

Значения элементов фильтров Чебышёва 2-9-го порядков при а=0,011дБ

п	C1	L2	C3	L4	C5	L6	С7	L8	С9
3	0,6395	0,9786	0,6395
4	0,6349	1,203	1,203	0,6349
5	0,7664	1,310	1,588	1,310	0,7664
6	0,7275	1,380	1,607	1,607	1,380	0,7275
7	0,8068	1,397	1,757	1,634	1,757	1,397	0,8068
8	0,7670	1,433	1,718	1,754	1,754	1,718	1,433	0,7670
9	0,8242	1,431	1,813	1,712	1,913	1,712	1,813	1,431	0,8242
n	L1	С2	L3	C4	L5	С6	L7	C8	L9

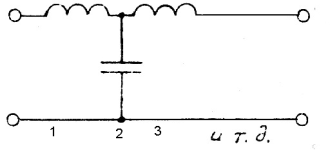
Таблица П. 1.3

Значения элементов фильтров Чебышёва 2-9-го порядков при а=0,028 дБ

п	C1	L2	C3	L4	C5	L6	С7	L8	С9
3	0,7750	1,0684	0,7750
4	0,8402	1,307	1,307	0,7402
5	0,8973	1,359	1,727	1,359	0,8973
6	0.8366	1,449	1,684	1,684	1,449	0,8366
7	0,9350	1,431	1,874	1,634	1,874	1,431	0,9350
8	0,8788	1,487	1,791	1,792	1,792	1,791	1,487	0,8788
9	0,9511	1,459	1,922	1,696	2,009	1,696	1,922	1,459	0,9511
n	L1	С2	L3	C4	L5	С6	L7	C8	L9

Таблица П. 1.4

Значения элементов фильтров Чебышёва 2-9-го порядков при а=0,044 дБ

п	C1	L2	C3	L4	C5	L6	С7	L8	С9
3	0,8533	1,1036	0,8533
4	0,7994	1,354	1,354	0,7994
5	0,9732	1,372	1,803	1,372	0,9732
6	0,8989	1,478	1,721	1,721	1,478	0,8989
7	1,010	1,437	1,941	1,622	1,941	1,437	1,010
8	0,9430	1,507	1,828	1,808	1,808	1,828	1,507	0,9430
9	1,025	1,462	1,985	1,677	2,066	1,677	1,985	1,462	1,025
n	L1	С2	L3	C4	L5	С6	L7	C8	L9

Таблица П. 1.5

Значения элементов фильтров Чебышёва 2-9-го порядков при а=0,099 дБ

п	C1	L2	C3	L4	C5	L6	С7	L8	С9
3	1,0285	1,1468	1,0285
4	0,9277	1,434	1,454	0,9277
5	1,144	1,372	1,972	1,372	1,144
6	1,036	1,516	1,788	1,788	1,516	1,036
7	1,178	1,423	2,094	1,574	2,094	1,423	1,178
8	1,086	1,526	1,902	1,830	1,830	1,902	1,526	1,086
9	1,193	1,443	2,132	1,618	2,203	1,618	2,132	1,443	1,193
n	L1	С2	L3	C4	L5	С6	L7	C8	L9

Таблица П. 1.6

Значения элементов фильтров Чебышёва 2-9-го порядков при а=0,177 дБ

п	C1	L2	C3	L4	C5	L6	С7	L8	С9
3	1,1893	1,1540	1,1893
4	1,041	1,482	1,482	1,041
5	1,302	1,346	2,129	1,346	1,302
6	1,159	1,529	1,838	1,838	1,529	1,159
7	1,335	1,389	2,240	1,515	2,240	1,389	1,335
8	1,215	1,523	1,963	1,840	1,840	1,963	1,523	1,215
9	1,349	1,405	2,274	1,551	2,339	1,551	2,274	1,405	1,349
n	L1	С2	L3	C4	L5	С6	L7	C8	L9

Таблица П. 1.7

Значения элементов фильтров Чебышёва 2-9-го порядков при а=0,28 дБ

п	C1	L2	C3	L4	C5	L6	С7	L8	С9
3	1,3451	1,1412	1,3451
4	1,146	1,513	1,513	1,146
5	1,456	1,307	2,283	1,307	1,456
6	1,277	1,528	1,878	1,878	1,528	1,277
7	1,488	1,343	2,388	1,451	2,388	1,343	1,488
8	1,340	1,508	2,019	1,844	1,844	2,019	1,508	1,340
9	1,502	1,357	2,420	1,481	2,480	1,481	2,420	1,357	1,502
n	L1	С2	L3	C4	L5	С6	L7	C8	L9

37