ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

ЗАБАЙКАЛЬСКИЙ ИНСТИТУТ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

ОДОБРЕНО КАФЕДРОЙ “Энергоснабжение ” Заведующий кафедрой _____________ С.А. Филиппов "___ "__________ 2011 г.

УТВЕРЖДАЮ: Декан факультета НТС ______________В.В. Степанов "___"__________ 2011 г.

Теория линейных электрических цепей ж.Д. Атс

Методические указания к лабораторным работам № 6-8

для студентов II-III курса специальности

190402. Автоматика, телемеханика и связь

НА ЖЕЛЕЗНОДОРОЖНОМ ТРАНСПОРТЕ (АТС)

Чита – 2011

Разработаны на основании примерной учебной программы данной дисциплины, составленной в соответствии с государственными требованиями к минимуму содержания и уровню подготовки инженера по специальности 190402 "Автоматика, телемеханика и связь на железнодорожном транспорте".

С о с т а в и т е л ь – к.т.н., доцент Менакер К.В.

© Забайкальский институт железнодорожного транспорта, 2011

Лабораторная работа №6

Определение реакции цепи на произвольное внешнее воздействие по ее переходной и импульсной характеристикам

Цель работы: получение навыков определения временных характеристик цепей и определения реакции цепи на произвольное внешнее воздействие с помощью интеграла Дюамеля.

1. Теоретические сведения

Переходной характеристикой линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи на воздействие неединичного скачка тока или напряжения к высоте этого скачка при нулевых начальных условиях:

(1)

Из выражения (1) следует, что , если , следовательно, переходная характеристика цепи численно равна реакции цепи на воздействие единичного скачка тока или напряжения.

Импульсной характеристикой линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи на воздействие бесконечно короткого импульса бесконечно большой высоты и конечной площади к площади этого импульса при нулевых начальных условиях:

(2)

Как следует из выражения (2), импульсная характеристика цепи численно равна реакция цепи на воздействие единичного импульса .

Переходная и импульсная характеристики связаны с операторной характеристикой цепи:

;

. (3)

При операторные изображения переходной и импульсной характеристик имеют простой вид:

; . (4)

Для определения переходных (импульсных) характеристик линейной цепи в общем случае необходимо рассмотреть переходные процессы, имеющие место в данной цепи при воздействии на нее единичного скачка (единичного импульса) тока или напряжения. Это может быть выполнено с помощью классического или операторного метода анализа переходных процессов. На практике для нахождения временных характеристик линейных цепей удобно использовать другой путь, основанный на применении соотношений, устанавливающих связь между частотными и временными характеристиками.

При этом сначала составляется операторная схема замещения цепи для нулевых начальных условий. Далее определяется операторная характеристика цепи . С использованием характеристики и выражений (3, 4) определяют искомые временные характеристики.

Пример. Для цепи, представленной на рис. 1, найдем переходную и импульсную характеристики в режиме холостого хода на зажимах .

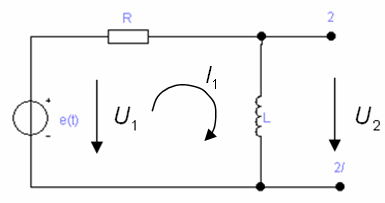
Рис. 1 К примеру

Используя метод контурных токов, составим уравнение для входного напряжения применительно к режиму холостого хода цепи:

,

Операторная характеристика цепи при рассмотрении реакции в виде тока:

Следовательно, операторные изображения переходной и импульсной характеристик в соответствии с выражениями (4) имеют вид:

Используя таблицы обратного преобразования Лапласа , переходим от изображений искомых временных характеристик к оригиналам:

; .

Заменяя в полученных выражениях на , находим временные характеристики цепи при :

; .

На рис. 2 представлен вид временных характеристик .

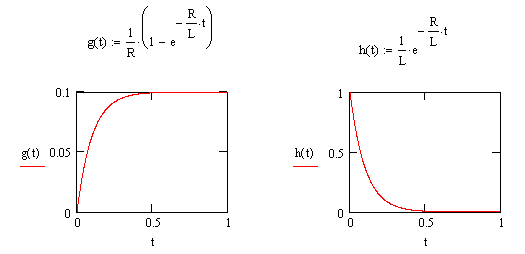
Рис. 2 Вид временных характеристик

В соответствии с определением переходной характеристики (1) реакция цепи на воздействие неединичного скачка, приложенного в момент времени , равна произведению высоты скачка на переходную характеристику цепи . Следовательно, реакция цепи на воздействие, представляемое суммой неединичных скачков, равна сумме произведений высот скачков на соответствующие переходные характеристики:

. (5)

Очевидно, что точность представления входного воздействия в виде суммы неединичных скачков, как и точность представления реакции цепи в виде (5), возрастает с уменьшением шага разбиения по времени . При суммирование заменяется интегрированием:

(6)

Выражение (6) известно под названием интеграла Дюамеля.

В соответствии с определением импульсной характеристики (2) реакция цепи на воздействие одиночного импульса равна произведению площади импульса на импульсную характеристику цепи :

(7)

Следовательно, реакция цепи на произвольное воздействие равна сумме произведений площадей импульсов на соответствующие импульсные характеристики :

. (8)

Устремляя к нулю и переходя от суммирования к интегрированию, окончательно получаем:

. (9)

Выражение (9) представляет собой одну из форм записи интеграла Дюамеля и его можно получить непосредственно из (6).

В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, при внешнем пилообразном воздействии.

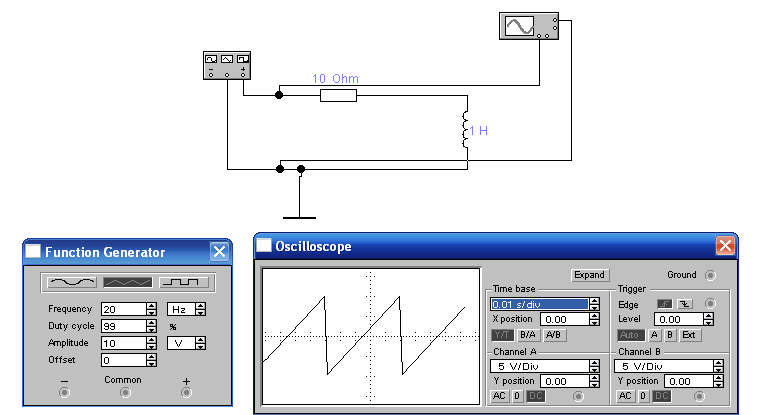
Рис. 3 К примеру

Аналитически представим входное воздействие на интервале :

.

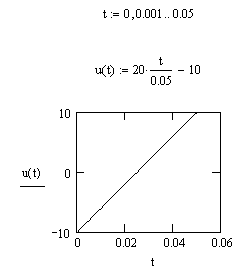
Рис. 4 Входное воздействие

Переходная характеристика:

.

Производная от входного воздействия:

Реакция цепи в виде тока цепи:

.

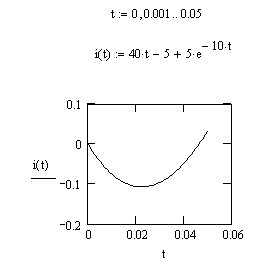
Рис. 5 Реакция цепи на входное воздействие

Импульсная характеристикам цепи:

.

Определим реакцию цепи с использованием импульсной характеристики цепи:

.

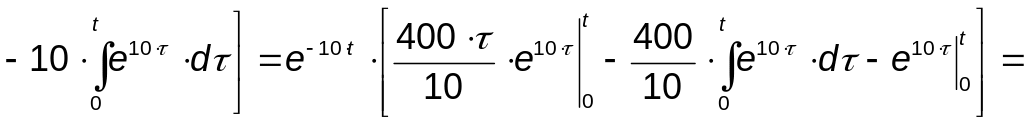
Как исследовало ожидать, выражения для реакции цепи на заданное воздействие, найденные с помощью импульсной характеристик цепи, совпадают с соответствующими выражениями, полученными с использованием переходной характеристики.

На рис. 6 представлена осциллограмма тока исследуемой цепи, полученная в программе EWB 5.12.

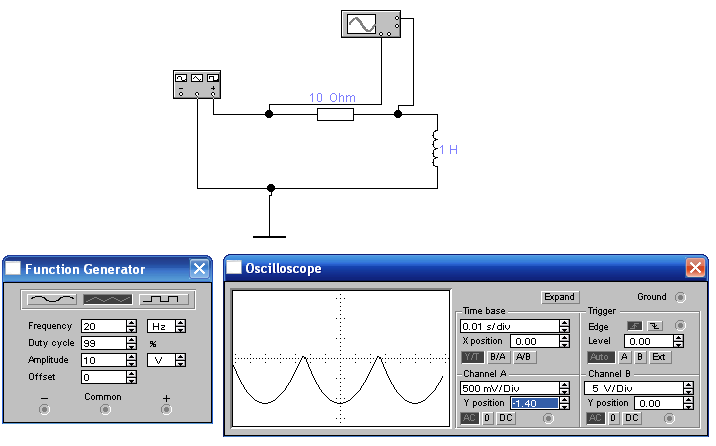
Рис. 6 Реакция цепи на входное воздействие