Последовательное соединение проводников

П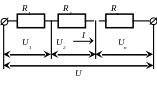 ри последовательном соединении n проводников полное сопротивление участка может быть определено с учётом выражения:

U = U₁ + U₂ + …+ U_n, (10)

являющегося следствием закона

Рис. 1 сохранения энергии.

Совместное решение уравнения (7) и уравнения (10), с учётом того, что ток J одинаков во всех элементах цепи приводит к выражению

R = R₁ + R₂ +…+ R_n, (11)

поэтому напряжения на отдельных участках цепи U_k пропорциональны сопротивлениям этих участков

.

Параллельное соединение проводников

П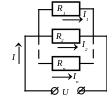 ри параллельном соединении проводников (рис. 2) напряжение на каждом из них одно и то же. По закону Ома для однородного участка цепи сила тока в проводнике будет:

J_k = . (12)

Рис. 2

Отсюда следует, что токи в ветвях обратно пропорциональны сопротивлениям

.

Полный ток равен сумме токов, протекающих в каждой из ветвей

J = J₁ + J₂ +… +J_n. (13)

Заметим, что формула (10) является следствием закона сохранения заряда.

Объединив формулы (9) и (10), нетрудно получить выражение для полного сопротивления R участка цепи из n параллельно соединенных проводников.

. (14)

Закон Ома для неоднородного участка цепи

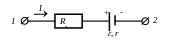
Рис. 3 а Рис. 3 б

Участок цепи, на котором действуют сторонние силы (например, имеются источники тока), называется неоднородным (рис. 3 а и рис. 3 б). На неоднородном участке цепи напряженность результирующего поля складывается из напряженности электростатического поля и напряженности поля сторонних сил :

= + . (15)

В результате, падение напряжения на участке 1-2 равно разности потенциалов между точками 1 и 2 плюс ЭДС (рис. 3 а) и минус ЭДС (рис. 3 б):

J (R_н + r) = ₁ -₂ ε. (16)

Формула (16) выражает закон Ома для неоднородного участка цепи. Здесь (R_н + r)- сопротивления участка цепи, R_н - сопротивление нагрузки, r - сопротивление источника тока. Знак перед ЭДС должен быть согласован с направлением тока (ЭДС положительна, если ток течет внутри источника от минуса к плюсу).

Закон Ома для замкнутой цепи

В случае замкнутой цепи (рис. 4) работа кулоновских сил равна нулю. Формально можно считать, что потенциалы точек 1 и 2 равны между собой ₁ = ₂ и поэтому разность потенциалов в формуле (13) равна нулю.

В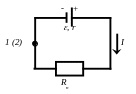 результате преобразования выражения (13), получаем закон Ома для замкнутой цепи

J ,

откуда

J = . (17)

Рис. 4

Разность потенциалов между клеммами источника тока совпадает с напряжением на нагрузке U, которое по закону Ома для однородного участка цепи равно U=JR_н, поэтому из формулы (17) следует, что

U=ε – Jr. (18)

При J=0 (в режиме холостого хода источника) напряжение на зажимах источника равно его ЭДС U= ε.

При включении нескольких одинаковых источников общий ток в цепи, в зависимости от вида их соединения (рис. 5 а последовательное соединение и рис. 5б параллельное соединение), можно определить по формулам (19) и (20).

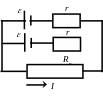
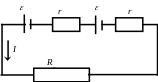
Рис. 5 а Рис. 5 б

J= , (19)

J=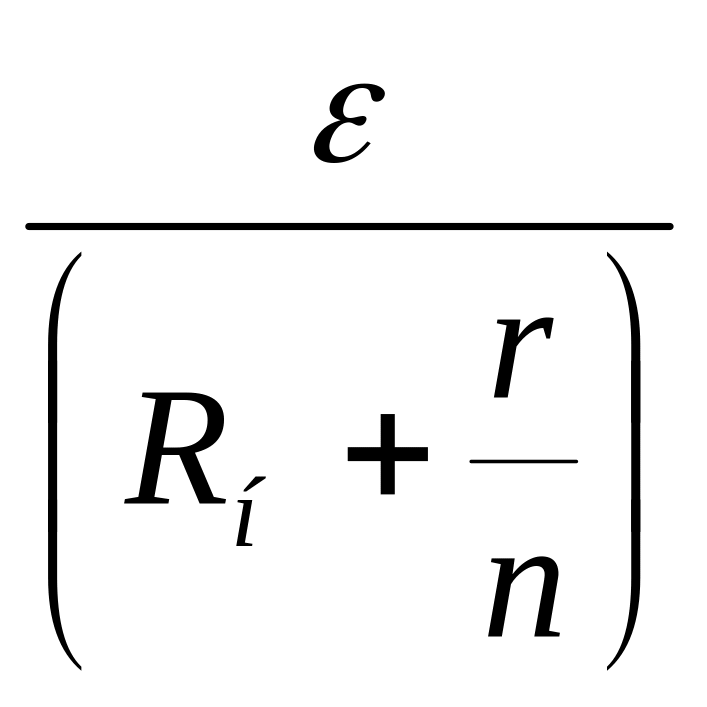 . (20)