Федеральное агентство по образованию

Муромский институт (филиал)

Государственного образовательного учреждения высшего профессионального образования

Владимирский государственный университет

Кафедра: Физика

Дисциплина: Физика

Лабораторная работа № 3.03

Утверждена на методическом

семинаре кафедры

___________Зав. кафедрой

Муром 2005 г.

Исследование характеристик возбужденных в струне стоячих волн

Цель работы: Изучение стоячих волн на струне с закрепленным концом, исследование зависимости скорости распределения поперечных волн в струне от ее нажатия.

Приборы и принадлежности: Струна, закрепленная на штативе, подставка для грузов и набор разновесов, генератор сигналов ГЗ-33, магнит, микрометр, масштабная линейка.

Теоретические сведения

Если в каком либо месте упругой среды возбудить колебания ее частиц, то вследствие взаимодействия между ними это колебание начнет распространятся в среде от частицы к частице. Процесс распространения колебаний в сплошной среде, периодический во времени и пространстве, называется волновым процессом (волной).

При распространении волны, частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице переносится лишь энергия без переноса веществ.

Выделяют следующие виды волн:

• Волны на поверхности жидкости;

• Упругие (механические);

• Электромагнитные.

Упругими называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные.

В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскости, перпендикулярной направлению распространения волны. Продольные волны могут распространятся в средах, в которых возникают упругие силы при деформациях сжатия и растяжения, то есть в твердых, жидких и газообразных телах. Сплошная среда, то есть непрерывно распределенная в пространстве и обладающая упругими свойствами.

Поперечные волны могут распространятся в среде, в которой возникают упругие силы при деформации сдвига, то есть фактически только в твердых телах. Волны, которые переносят в пространстве энергию называют бегущими (в отличие от стоячих волн).

Стоячие волны – волны, образующиеся при наложении двух бегущих синусоидальных волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Для вывода уравнения стоячей волны, предположим, что две бегущие синусоидальные волны распространяются навстречу друг другу вдоль оси в среде без затухания, причем, обе имеют одинаковые амплитуды и частоты. Начало координат выбирают в точке, в которой обе волны имеют одинаковую фазу, отсчет времени начнем с момента, когда фазы обеих волн равны нулю. Тогда уравнение волны распространяющейся вдоль положительного направления оси х и волны распространяющейся навстречу будут иметь вид:

ξ ₁=A·cos(ωt-kx)

ξ₂=A·cos(ωt+kx) (1)

Сложив эти два уравнения и учитывая, что (волновое число), получим уравнение стоячей волны:

(2)

Из уравнения стоячей волны вытекает, что в каждой точке стоячей волны происходит колебание той же частоты  c амплитудой зависящей от координаты х точки.

В точках среды, где:

, (m=0,1,2,3,…) (3)

амплитуда стоячей волны достигает максимального значения, равного 2А. В точках среды, где:

, (m=0,1,2,3,…) (4)

амплитуда стоячей волны обращается в нуль. Точки, в которых амплитуда стоячей волны максимальна A_cm=2A, называются пучностью стоячей волны. Точки в которых амплитуда стоячей волны равна нулю A_cm=0, называются узлами стоячей волны. Из формул (3) и (4) получим координаты пучностей и узлов:

, (m=0,1,2,…) (5)

, (m=0,1,2,…) (6)

Из (5) и (6) следует, что расстояние между двумя соседними пучностями и двумя соседними узлами одинаковы и равны.

Образование стоячих волн наблюдается обычно при интерференции бегущей и отображенной волны. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образовывать стоячую волну. На границе, где происходит отражение в данном случае будет узел. Будет ли на границе отражения узел (амплитуда волны минимальна) или пучность (амплитуда волны максимальна), зависит от отношения плотностей сред. Если среда, от которой происходит отражение менее плотная, то в месте отражения получается пучность (рис.1а), если более плотная, то получается (рис.1б) узел:

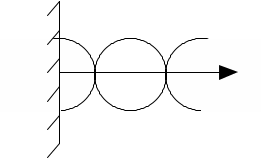
а) б)

Рисунок 1

Образование узла связано с тем, что волна, отражаясь от более плотной среды меняет фазу на противоположную и у границы происходит сложение колебаний противоположных направлений, в результате чего получается узел.

Если же отражается от менее плотной среды, то изменение фазы не происходит. В стоячей волне нет переноса энергии, то есть падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия стоячей волны, заключенная между узловыми точками остается постоянной. И лишь в пределах расстояний, равных /2 происходит взаимное превращение кинетической энергии в потенциальную и обратно.

В закрепленной с обеих сторон струне при распределении в ней поперечных колебаний устанавливаются стоячие волны, причем в месте закрепления струны располагаются узлы. Вследствие этого в струне возбуждаются колебания только таких частот, при которых на длине струны l укладывается целое число полуволн. Отсюда следует условие:

или (n=1,2,3,…) (7)

Учитывая связь длины волны колебаний с частотой и скоростью распространения волны v, можно записать:

(9)

Частоты _n называются собственными частотами колебаний струны. Самая низкая собственная частота называется основной частотой или основным тоном. Более высокие частоты, кратные основной частоте называются обертонами или гармониками (n = 2 – первый обертон, n = 3 – второй обертон и т.д.).

Скорость распространения поперечных волн вдоль струны зависит от натяжения струны и определяется по формуле:

(10)

где P – натяжение струны;

 – плотность материалы струны;

d – диаметр струны.

В настоящей работе определяются собственные частоты струны, производится соблюдение формы собственных колебаний, а также исследуется зависимость скорости распространения поперечных колебаний в струне от натяжения.

Для возбуждения колебаний в струне в данной работе используется метод резонанса. В случае, когда сила возбуждающая колебания, изменяется по гармоническому закону, установившиеся вынужденные колебания имеют частоту, равную частоте вынуждающей силы. Явление резонанса заключается в следующем: если частота вынуждающей силы, приложенной к малому участку струны совпадает с одной из собственных частот струны, а ее место приложения с одной и пучностей соответствующей стоячей волны, в струне устанавливается стоячая волна с максимальной амплитудой колебаний.