8.2 Антагонистические игры.
Прежде всего, надо уметь находить верхнюю и нижнюю цены игры, т.к. достаточно много игр решается в чистых стратегиях.
Найти нижнюю и верхнюю цены игры для матрицы
Ai |
Bj |
αi α=max αi |
||
B1 |
B2 |
B3 |
||
A1 |
0.4 |
0.6 |
0.8 |
0.4 |
A2 |
1.1 |
0.7 |
0.9 |
0.7 |
A3 |
0.7 |
0.3 |
0.5 |
0.3 |
βJ β = min βJ |
1.1 |
0.7 |
0.9 |
|
Для этой матрицы видно, что α = β = 0,7 = (А2, В2).
Общее значение нижней и верхней цены игры α = β = ν называется чистой ценой игры. Седловой точке соответствует пара минимаксных стратегий (А2В2), эти стратегии называются оптимальными, а их совокупность - решением игры (γ = 0,7).
Если седловой точки нет, то можно применить графический способ для задач (2 × n, m × 2 ) или (если m>2 и n >2)составить математическую модель задачи линейного программирования и решить ее симплекс-методом.
Здесь m – число стратегий игрока А, n – число стратегий игрока В.
Геометрический метод решения задач теории игр
Геометрический метод решения игр с нулевой суммой применяется к играм, где хотя бы у одного игрока имеется только две стратегии. Иногда возможно упростить платежную матрицу игры, применяя следующие принципы:
1. Игрок А стремится увеличить свой выигрыш, поэтому он не будет использовать стратегии, которые заведомо дают ему меньшие выигрыши;
2. Игрок В стремится уменьшить свой проигрыш, поэтому он не будет использовать стратегии, которые заведомо дают большие проигрыши.
Р
ассмотрим
платежную матрицу
-
7
6
5
4
2
5
4
3
2
3
5
6
6
3
5
2
3
3
2
4
Упростим матрицу, вычеркивая заведомо невыгодные стратегии игроков, начиная с игрока А, а затем игрока В.
Путем упрощения, ее можно свести к матрице (2 * 2)
-
ВJ АJ
В1
В2
A1
4
2
A2
3
5
р1 - вероятность применения игроком А стратегии A1;
р2 - вероятность применения игроком А стратегии A2.
Так как р1+ р2=1, то р2=1- р1. Тогда получим:
Чистые стратегии игрока В |
Ожидаемые выигрыши игрока А |
В1 |
4 р1+3 р2= (4-3)р1+3=р1+3 |
В2 |
2 р1+5 р2=(2-5)р1+5=-3р1+5 |
На оси Ох разместим точки р1=0 и р1=1, через которые проведем прямые, перпендикулярны оси Ох. Подставляя р1=0 и р1=1 в выражение р1+3, найдем значения, которые отложим на соответствующих перпендикулярных прямых. Соединив эти точки, получим прямую.
Аналогично рассмотрим выражение -3р1+5.
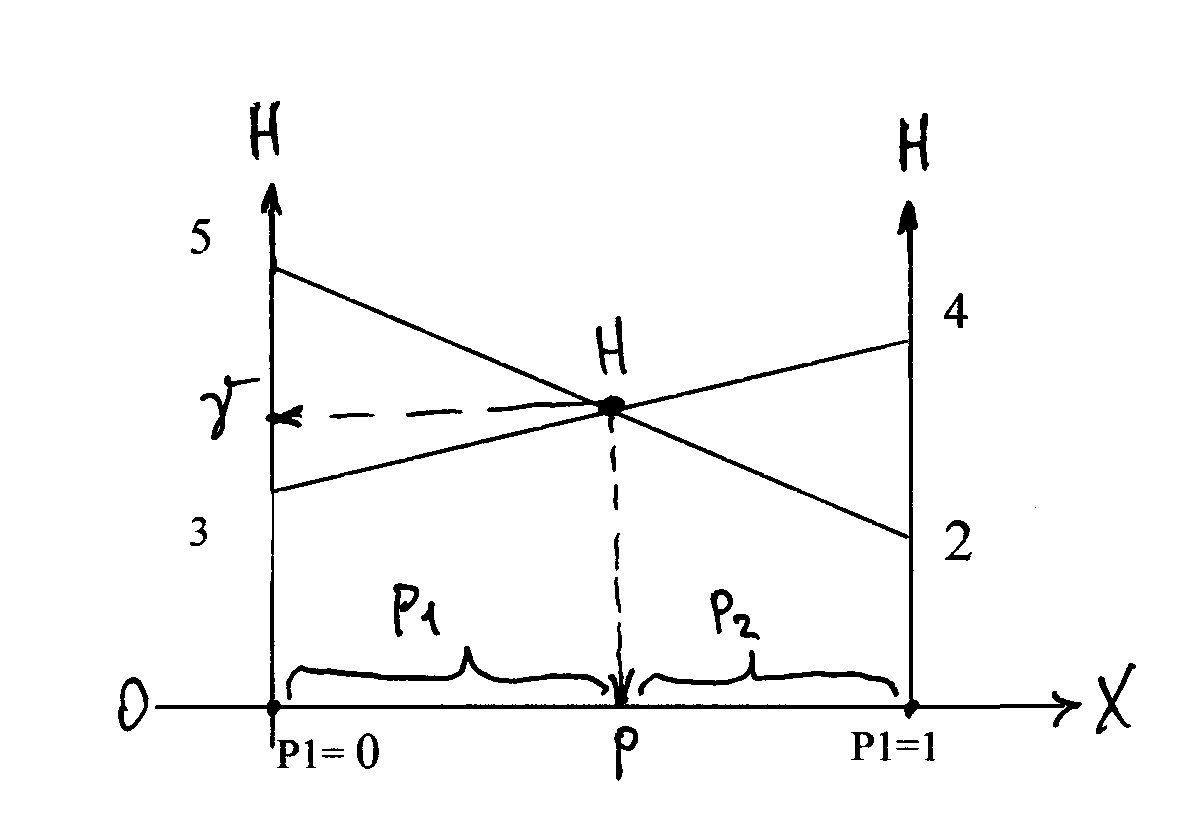
Оптимальная стратегия первого игрока найдется из равенства выражений
р1+3 и -3р1+5: р1= р2=0,5. SA = (0,5; 0; 0,5; 0), при этом цена игры равна 3,5.
Для второго игрока оптимальная стратегия ищется аналогично.
Если же игра не сводится путем упрощения к 2 x n или m x 2, то составляется математическая модель и задача решается симплекс-методом.