28. Методы расчета цифровых рекурсивных фильтров: инвариантное преобразование импульсной характеристики, билинейное z-преобразование

Метод инвариантного преобразования (инвариантности) импульсивной характеристики

Метод синтеза цифровых фильтров, основанный на использовании импульсной характеристики аналогового фильтра-прототипа, называют методом инвариантного преобразования (инвариантности) импульсной характеристики. Для более наглядного представления эта процедура приведена на рис.3.5. Эта процедура устанавливает, что импульсная характеристика h(n) результирующего цифрового фильтра представляет собой дискретизированную импульсную характеристику h(t) соответствующего аналогового фильтра и определяется следующим образом:

, (3.13)

где Т – интервал дискретизации.

Процедура расчета по методу инвариантного преобразования импульсной характеристики.

Применяя затем к импульсной характеристике цифрового фильтра z-преобразование, можно найти передаточную функцию и составить алгоритм цифровой фильтрации.

Определим необходимую для данного метода замену комплексной переменной s на z в передаточной функции аналогового фильтра (процедуру перехода).Для этого разложим передаточную функцию Н(s) исходного аналогового фильтра на простые дроби:

, (3.14)

где: N > M 0, b_N 0, b₀ 0, а все полюсы различны.

Кроме того, для всех ί = 1,2…, N, представляет собой ί- ый полюс аналогового фильтра, а _i - вычет функции Н(s) в полюсе . Импульсную характеристику h(t) аналогового фильтра можно получить, если найти обратное преобразование Лапласа выражения (3.14). В результате получим:

, (3.15)

Подставив (3.15) в (3.13), получим импульсивную характеристику h(n) соответствующего цифрового фильтра:

· , (3.16)

Передаточная функция Н(z) результирующего цифрового фильтра определяется путем нахождения z-преобразования импульсной характеристики, заданной выражением (3.16), следующим образом:

· .

Изменив порядок суммирования и просуммировав по n, получим:

. (3.17)

Сравнивая выражения (3.14) и (3.17), можно получить соотношение перехода от аналоговых фильтров к цифровым для метода инвариантного преобразования импульсной характеристики:

, (3.18)

где – полюс цифрового фильтра, соответствующий полюсу аналогового фильтра.

БИХ - фильтры высоких порядков обычно реализуются на основе последовательного или параллельного соединения биквадратных блоков. Следовательно, особый интерес представляет случай N=2. В этом случае преобразование (3.17) имеет вид

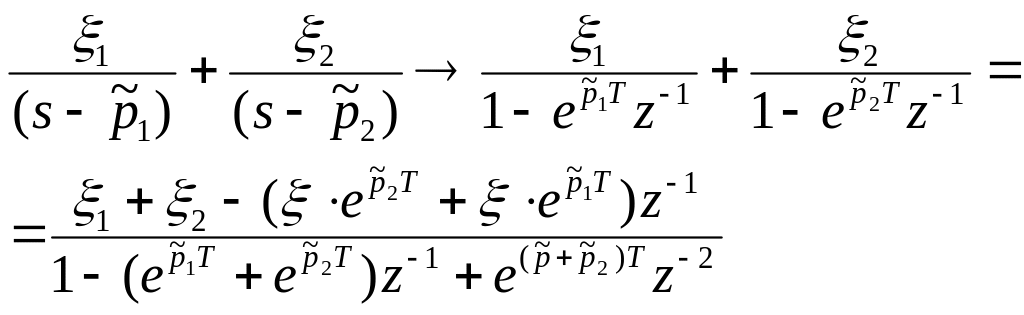
Исследование метода инвариантности на соответствие двум необходимым условиям процедуры перехода (3.2) и (3.3) показывает, что горизонтальная полоса шириной в s-плоскости отображаются соответственно на всю z-плоскость, т.е. левая и правая половины этой полосы отображаются соответственно в части z-плоскости внутри и вне единичной окружности, а мнимая ось – в единичную окружность. Поэтому все сложные полосы из s-плоскости шириной будут при отображении накладываться друг на друга в z-плоскости (рис.3.6).

Рис. 3.6 Свойства процедуры перехода на основе инвариантности импульсной характеристики

Отсюда следует, что для того, чтобы частотные характеристики исходного аналогового фильтра и рассчитываемого методом инвариантного преобразования импульсной характеристики цифрового фильтра соответствовали друг другу, необходимо, чтобы полоса пропускания аналогового фильтра находилась в пределах диапазона . Другими словами, из-за эффекта наложения метод инвариантности импульсной характеристики применим только для аналоговых фильтров с существенно ограниченной частотной характеристикой, которая удовлетворяет условию:

|H(jω)| 0 для |ω|>ω_в,

т.е. в случае нижних частот и полосовых, с достаточно резким срезом АЧХ.

Метод билинейного Z-преобразования

Для исключения эффекта наложения, присущего методу инвариантного преобразования импульсной характеристики, необходимо определить однозначное непрерывное отображение из s-плоскости в z-плоскость. Одним из таких преобразований является билинейное z-преобразование, при котором для преобразования характеристики аналогового фильтра H(s) в характеристику эквивалентного цифрового фильтра применяется следующая схема:

где или

С помощью несложных преобразований можно найти обратное соотношение:

или

.

Для билинейного z-преобразования выполняются оба условия перехода. В этом случае мнимая ось I_m[s] s-плоскости полностью отображается в единичную окружность на z-плоскости, а левая полуплоскость s-плоскости отображается на z-плоскости внутрь единичного круга. Другими словами, физически реализуемый устойчивый аналоговый фильтр преобразуется с помощью билинейного преобразования в физически реализуемый устойчивый цифровой фильтр.

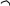
Можно также показать, что билинейное преобразование – однозначная функция. Это означает, что каждой точке в z-плоскости соответствует только одна точка в s-плоскости и наоборот. Из этого свойства следует, что при билинейной процедуре преобразования отсутствует эффект наложения.

Методики расчета ЦФ на основе метода билинейного преобразования сводится к нахождению подходящей передаточной функции Н(s) аналогового фильтра и применения к ней соответствующей замены комплексной переменной для получения передаточной функции Н(z) требуемого цифрового фильтра

,

При этом преобразовании, как уже отмечалось, будут сохраняться частотная характеристика и свойства устойчивости аналогового фильтра.

Тем не менее, следует отметить, что это не означает того, что частотные характеристики аналогового и цифрового фильтра будут полностью идентичными. Одинаковой на самом деле оказывается только их «форма». Это объясняется тем, что цифровая частота θ= Т и аналоговая частота ω связаны нелинейным соотношением:

, или

Действительно, подставляя в выражение

, и ,

получим

Отсюда легко получить предыдущее выражение.

Рис. Связь между аналоговой и цифровой частотой, иллюстрирующая эффект деформации

Связь аналоговой частоты и цифровой в этом случае почти линейна при малых значениях , но становится нелинейной при больших значениях , что приводит к искажению (или деформации) цифровой частотной характеристики. Для компенсации этого эффекта аналоговый фильтр (его одна или несколько критических частот) обычно предварительно деформируется перед применением билинейного преобразования. Например, при разработке фильтра нижних частот предварительной деформации подвергается частота среза или граничная частота:

где - заданная частота среза;

- деформированная частота среза;

или

T - интервал дискретизации

Несмотря на это метод билинейного преобразования дает лучшие результаты перехода от аналоговых фильтров к цифровым по сравнению с методом численного интегрирования и методом инвариантности импульсной характеристики, и является, пожалуй, самым важным методом получения коэффициентов БИХ - фильтров.

Для стандартных частотно-избирательных БИХ – фильтров можно следующим образом обобщить порядок применения билинейного преобразования.

1. На основе требований к цифровому фильтру определить нормированный аналоговый фильтр-прототип с передаточной функцией H(s).

2. Определить и деформировать граничные или критичные частоты нужного фильтра. Для нижних или верхних частот существует единственная граничная частота (частота среза) . Для полосовых и режекторных фильтров имеется верхняя и нижняя граничные частоты полосы пропускания 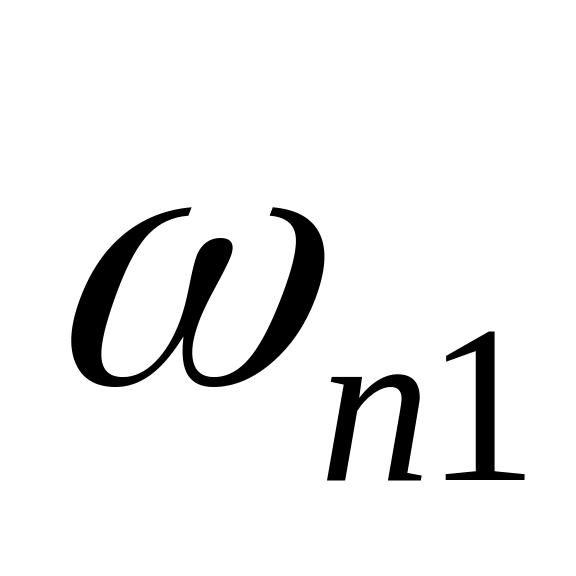и 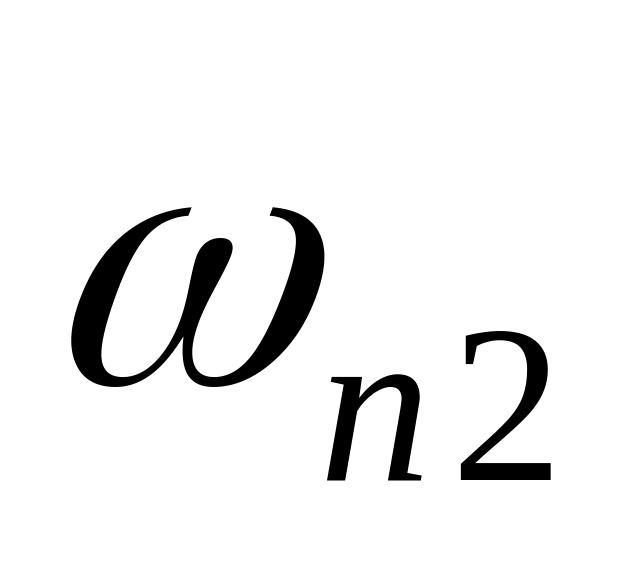, каждую из которых необходимо деформировать (могут также задаваться граничные частоты полосы затухания ):

3. Денормировать аналоговый фильтр-прототип, заменив s в передаточной функции H(s) с помощью одного из следующих преобразований (в зависимости от требуемого фильтра):

4. Применить билинейное z-преобразование и получить передаточную функцию нужного цифрового фильтра H(z), заменив s в денормированной передаточной функции H`(s):

Следует отметить, что деформирование частотной шкалы и билинейное z-преобразование для повышения вычислительной эффективности можно объединить в одно преобразование:

Далее, для ФНЧ и ФВЧ порядок H(z) равен порядку передаточной функции H(s) аналогового фильтра. Например, если функция H(z) получена из функции H(s) аналогового фильтра второго порядка, то и H(z) также будет описывать систему второго порядка. Для полосовых и режекторных(заградительных) фильтров порядок H(z) будет вдвое больше порядка H(s).

Пример. Фильтр нижних частот. Требуется разработать цифровой фильтр нижних частот, аппроксимирующий следующую передаточную функцию H(s) аналогового фильтра

Используя метод билинейного z-преобразования, получим передаточную функцию H(z) цифрового фильтра, если частота среза по уровню 3 дБ равна 150 Гц, а частота дискретизации равна 1,28кГц.

Решение. Предварительно деформируем частоту среза аналогового фильтра рад /с:

где

Промасштабированный аналоговый фильтр характеризуется передаточной функцией

После применения билинейного z-преобразования получим:

Отсюда легко найти собственные разностные уравнения и структурную схему полученного цифрового фильтра.