3.2. Линии тока, трубка тока, траектории и струйка

При анализе движения жидкости методом Эйлера геометрической характеристикой движения служит линия тока. Линия тока −это линия, касательные к которой в любой точке совпадают с направлением вектора скорости частицы жидкости в данной точке. Для её построения выберем в пространстве, занятом движущейся жидкостью, некоторую точку A₁ (рис.1а) и проведем в этой точке отвечающий ей в данный момент времени вектор скорости ₁. Затем возьмем точку А₂, лежащую на векторе ₂ вблизи точки A₁, и про­ведем вектор скорости ₂, относящийся к тому же самому моменту времени, и т.д. Получим ломаную линию А₁А₂А₃….., которая в пределе (при большом количестве точек, бесконечно близких друг к другу) обратится в кривую, которая и будет линией тока. В случае нестационарного потока линии тока отражают мгновенную картину движения жидкости, отвечающую определенному моменту времени. Касательные к линии тока фиксируют направления скорости разных частиц (А_1,А_2,А₃) в последовательных точках пространства в один и тот же момент времени t=t₁. Касательные к траектории дают направление скорости одной и той же частицы (А₁) в последовательные моменты времени (t_1, t₂, t₃). Траектория частицы А₁ имеет лишь одну общую точку с линией тока, отвечающей моменту времени t=t₁ (рис.1б).

При стационарном движении линии тока для различных моментов времени совпадают и вместе с тем имеют место их совпадения с траекториями. Это легко понять, если учесть, что каждая частица в любой точке, лежащей на её траектории, имеет то же направление ( и величину ) скорости, что и все остальные частицы, проходящие через эту точку. Действительно, пусть кривая на рис.1 представляет траекторию частицы А₁. В точке I, через которую эта частица проходит в момент времени t₁ , вектор скорости будет U_A1(t₁). Но в силу стационарности потока такую же скорость (по величине и направлению) будет иметь и частица A₂, проходящая через точку I в другой момент времени t₂, когда частица А₁, следуя вдоль своей траектории, окажется в точке 2. Таким образом, в один и тот же момент времени t₂ две частицы А₁ и А₂ оказываются на одной и той же траектории, следовательно, эта кривая является одновременно и линией тока.

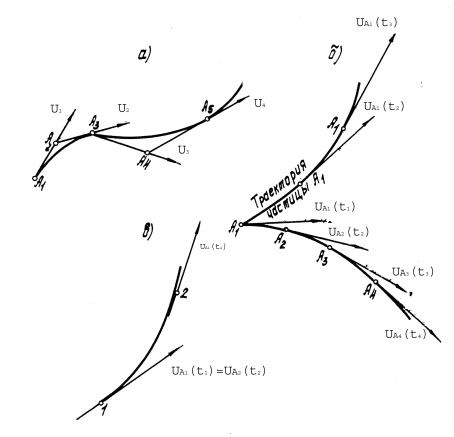
Рис.1

3.3. Уравнение линии тока

Уравнение линии тока легко составить, пользуясь такими рассуждениями. Допустим, что в данный момент времени имеем плос­кую линию тока а (рис.2).

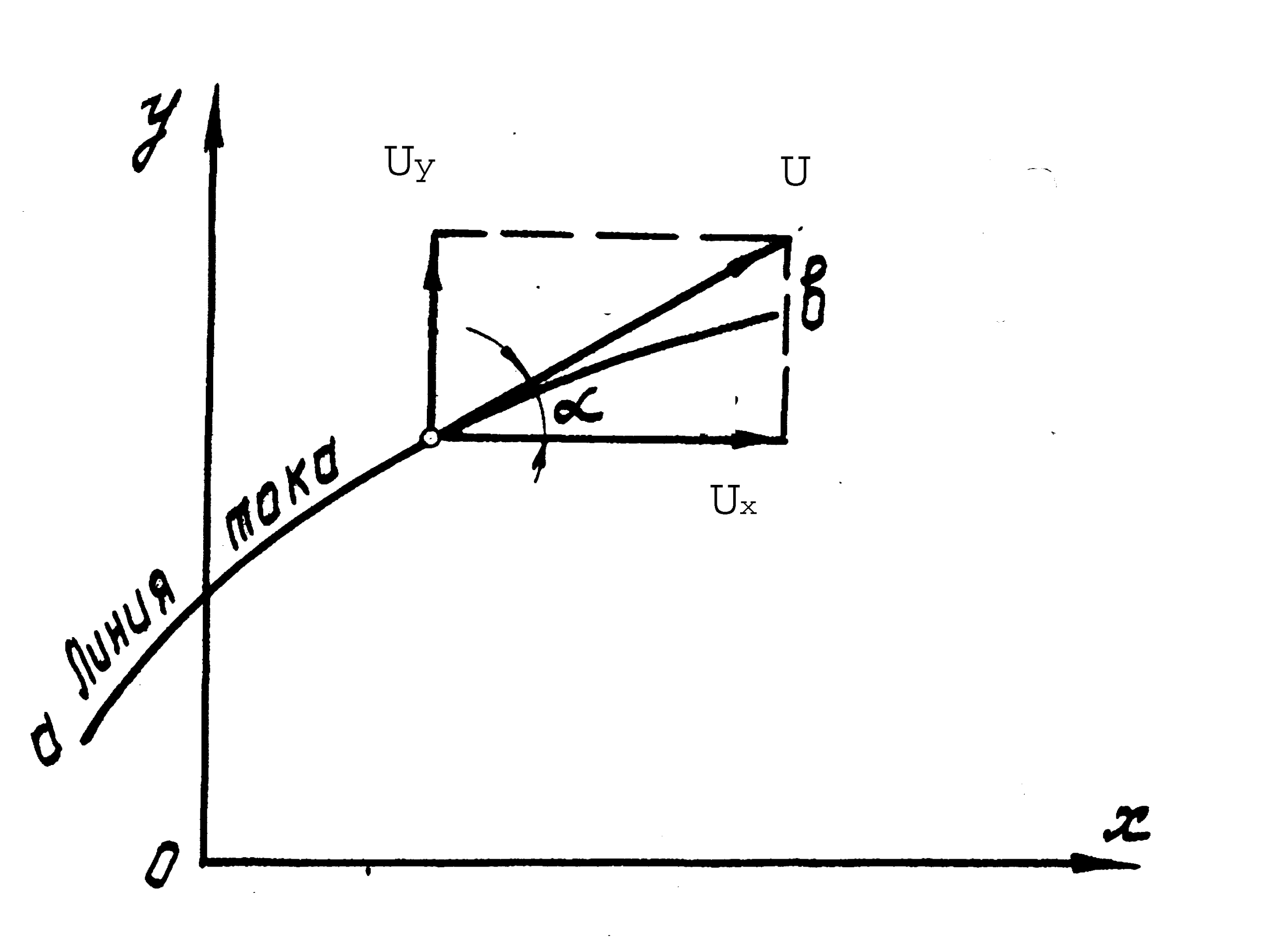
Рис.2

Очевидно, уравнение этой линии можно записать так:

y = f(x),

где x и y − координаты точек данной линии.

Непосредственно из рис.2 имеем U_Y/U_X = tg , а дифференцируя уравнение линии тока по x, находим

.

Таким образом, , или

, или ,

что и является уравнением линии тока в дифференциальном виде.

При пространственном движении дифференциальные уравнения линии тока записываются так: ,

или

. (3.10)

Проинтегрировав уравнения (3.10), можно получить уравнение линии тока в конечном виде. Решение этой системы может быть записано в виде двух общих интегралов:

;

,

где С₁ и С₂ −произвольные постоянные интегрирования.

Каждый из интегралов представляет в геометрическом отношении семейство поверхностей, зависящих от постоянных С₁ и С₂. Линия тока, отвечающая определенным значениям этих постоянных, находится как линия пересечения двух соответствующих поверхностей.

Если внутри движущейся жидкости выделить некоторый замкнутый контур L (рис.3) и через все его точки провести для данного момента времени линии тока, то они образуют поверхность, называемую поверхностью тока. На рис.3 представлена схема струйки в непрерывном потоке.

Рис.3

Часть жидкости, ограниченная этой поверхностью, получила название трубки тока.

В нестационарном потоке форма трубок тока непрерывно изменяется, поскольку изменяется направление линии тока. Важнейшим свойством трубки тока является непроницаемость её боковой поверхности для движущихся частиц жидкости, что легко понять, если учесть, что эта поверхность образована линиями тока.

Наряду с трубкой тока в гидродинамике пользуются еще понятием струйки. Струйкой называют часть жидкости, ограниченной поверхностью, образованной совокупностью траекторий, проходящих через все точки замкнутого контура. Для стационарного потока понятия трубки тока и элементарной струйки идентичны, так как линии тока и траекторий в этом случае совпадают.

Струйка имеет малую площадь поперечного сечения (в пределе ), которая может меняться по длине.

Совокупность элементарных струек образует поток жидкости.