2.9. Плавание тел

Закон Архимеда. Открыт за 250 лет до н.э. Характеризует плавучесть тела, погруженного в жидкость. Этот закон гласит: "Результирующая сила давления Р жидкости на погруженное в нее тело равна по величине весу жидкости в объеме погруженного в нее тела и “направлена по вертикали снизу вверх” (рис.11).

Рис.11

Видно, что , а

;

dP = dP_1Z -dP_2Z .

.

Знак минус указывает на то, сила P направлена снизу вверх.

Плавучесть тела. Если вес погруженного в жидкость тела G меньше архимедовой силы, т.е. P= gW > G, тело всплывает. Если Р < G, тело тонет. При P=G= W тело не тонет и не всплывает, находясь в состоянии покоя в любой точке водного пространства.

Следовательно, когда Р > G, то только часть тела погру­жена в жидкость, что характеризует его плавучесть. В этом случае архимедова сила P_n равна весу жидкости в объеме погруженной в нее части тела W, где − коэффициент, определяющий часть тела, погруженную в жидкость ( < 1),

P_n = g W = G_n . (2.42)

Вес жидкости в объеме погруженной в нее части тела g W называется водоизмещением. Центр давления при плавании, т.е. точка приложения архимедовой силы, называется центром водоизмещения. При качке судна центр давления меняет свое положение, т. к. в этом случае одна часть судна погружается в воду, а противоположная, на­оборот, выходит из воды. Это меняет форму подводной части судна и, следовательно, положение центра давления. Водоизмещение опре­деляет максимальную величину погружения судна в воду и его грузо­подъемность.

Водоизмещение некоторых судов и понтонов:

супертанкер "Крым"− 160 000 т (1974 г.),

атомный ледокол "Ленин"− 16000 т,

понтоны для подъемам затонувших судов− от 40 до 400 т.

Линия пересечения свободной поверхности водоема с боковой поверхностью судна при его максимальной нагрузке называется ватерлинией, а плоскость в пределах судна, ограниченная ватерлинией, − плоскостью плавания (рис.12).

Вертикальная ось симметрии 0-0, нормальная к плоскости плавания и обязательно проходящая через центр тяжести с плавающего тела или судна, называется осью плавания. Центр тяжести сухогрузного судна (неналивного) не меняет своего положения при качке. У наливных судов, имеющих свободную поверхность залитой жидкости, центр тяжести при качке перемещается.

Остойчивость плавающего тела. Плавающее тело при качке может наклоняться в ту или другую сторону или, как обычно говорят, давать крен. 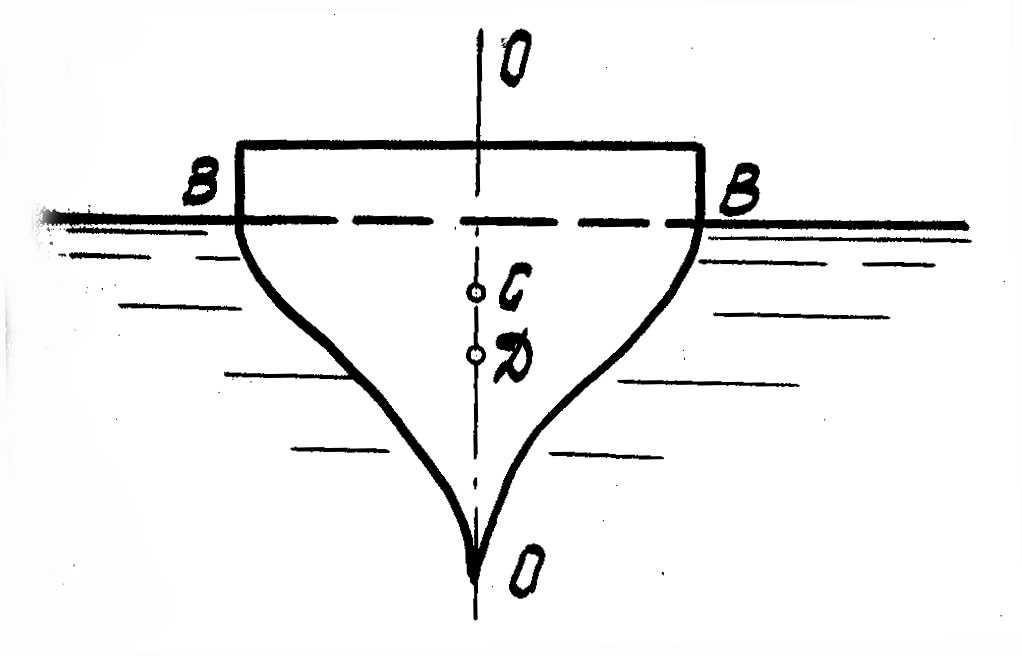Способность судна возвращаться из крена в первоначальное положение называется остойчивостью судна.

Плавающее тело или судно имеет на оси плавания 0-0 три характерные точки (рис.13): центр тяжести С, центр давления Д и метацентр М. Метацентром называется точка пересечения оси плавания с линией действия архимедовой силы при крене плавающего тела или судна.

Рис.12

Как уже было отмечено, центр давления при крене судна перемещается, поэтому и положение метацентра не может оставаться постоянным. Однако при кренах, не превышающих = 15°, положение метацентра почти не меняется и его принимают неизменным. В этом случае центр давления или водоизмещения Д перемещается примерно по дуге (с углом = 15°) окружности радиусом r_m, описанной из метацентра М. Радиус r_m, называется метацентрическим радиусом.

П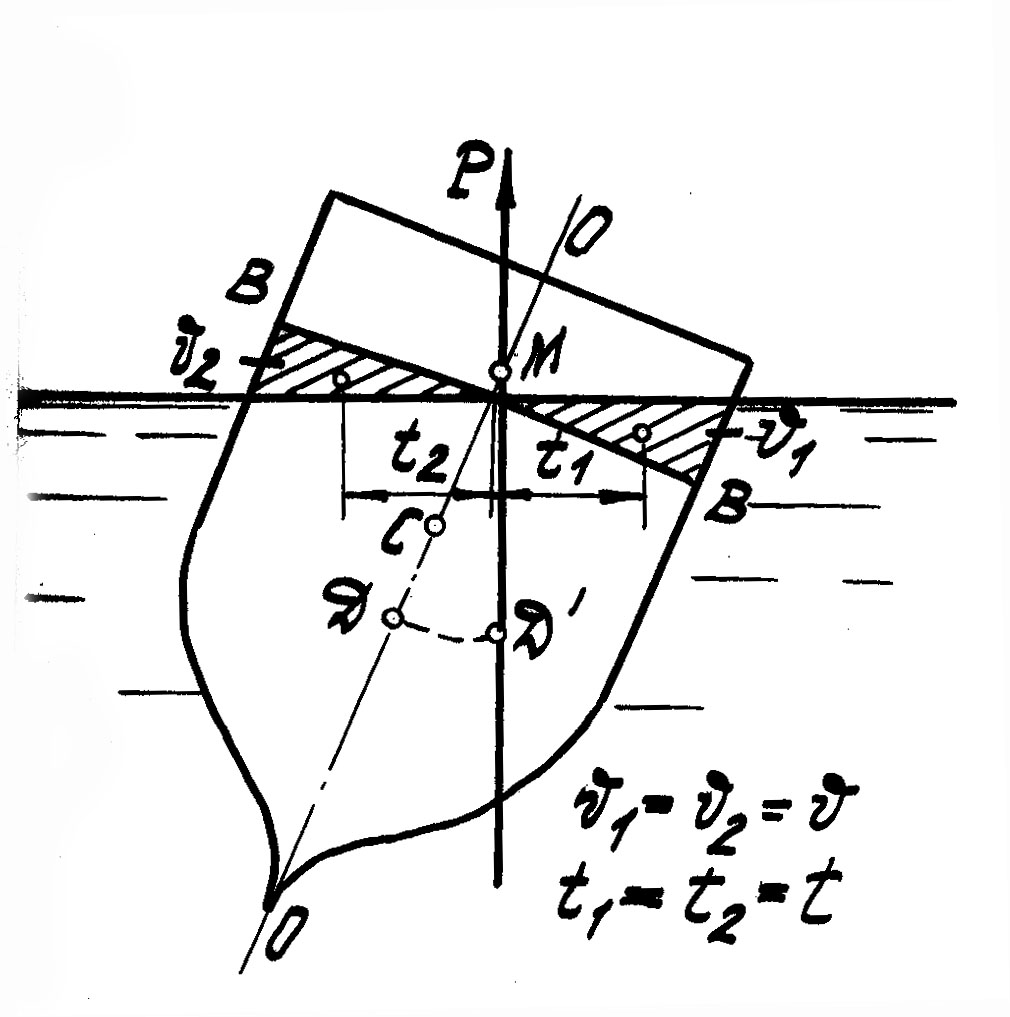 ри углах крена > 15° центр водоизмещения перемещается по некоторой кривой Д' Д" Д"' и т.д., отличной от дуги окружности, и метацентр уже не сохраняет своего постоянного положения (рис.14).

Остойчивость судна зависит от относительного положения центров Д, С и М.

Рассмотрим остойчивость для трех различных случаев относительного Рис.13 положения центров С и М (рис.15).

В случаях а и б судно остойчиво, так как действие пар сил Р и G препятствует крену. В случае же в остойчивость судна не обеспечена (судно опрокинется), т.к. пара сил Р и G увеличивает крен судна.

Р азличное влияние этих пар сил на остойчивость плавающих тел зависит от взаимного положения центра тяжести С и мета­центра М : если метацентр выше центра тяжести, судно остойчиво, если же метацентр ниже центра тяжести, судно неостойчиво.

Остойчивость можно характеризовать соотношением r_m и l: при r_m > l судно остойчиво, а при r_m < l судно неостойчиво. Заметим, что l > 0 , когда Д ниже С, и l < 0, когда Д выше С. Величина m, выражающая превышение метацентра над центром тяжести (m=r_m-l), называется метацентрической высотой.

Рис.14

Для остойчивости судна или тела необходимо, чтобы метацент­рическая высота имела положительное значение, т.е., если m > 0 , тело остойчиво, если же m < 0, тело неостойчиво.

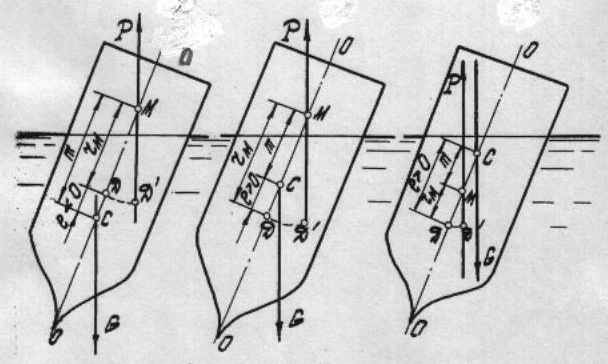
Рис.15