2.7. Эпюры гидростатического давления

В ряде случаев для наглядности целесообразно пользоваться диаграммами распределения гидростатического давления по смоченной поверхности. Такие диаграммы называют эпюрами гидростатического давления.

Рассмотрим прямоугольную стенку шириной в, наклоненную под углом к горизонту. Изобразим эту стенку в аксонометрии (рис.8).

Манометрическое (избыточное) давление р в точке А равно нулю, а в точке В равно .

Поскольку гидростатическое давление всегда нормально к смоченной поверхности стенки, то отрезок, равный , откладываем на перпендикуляре, восстановленном к стенке в точке В.

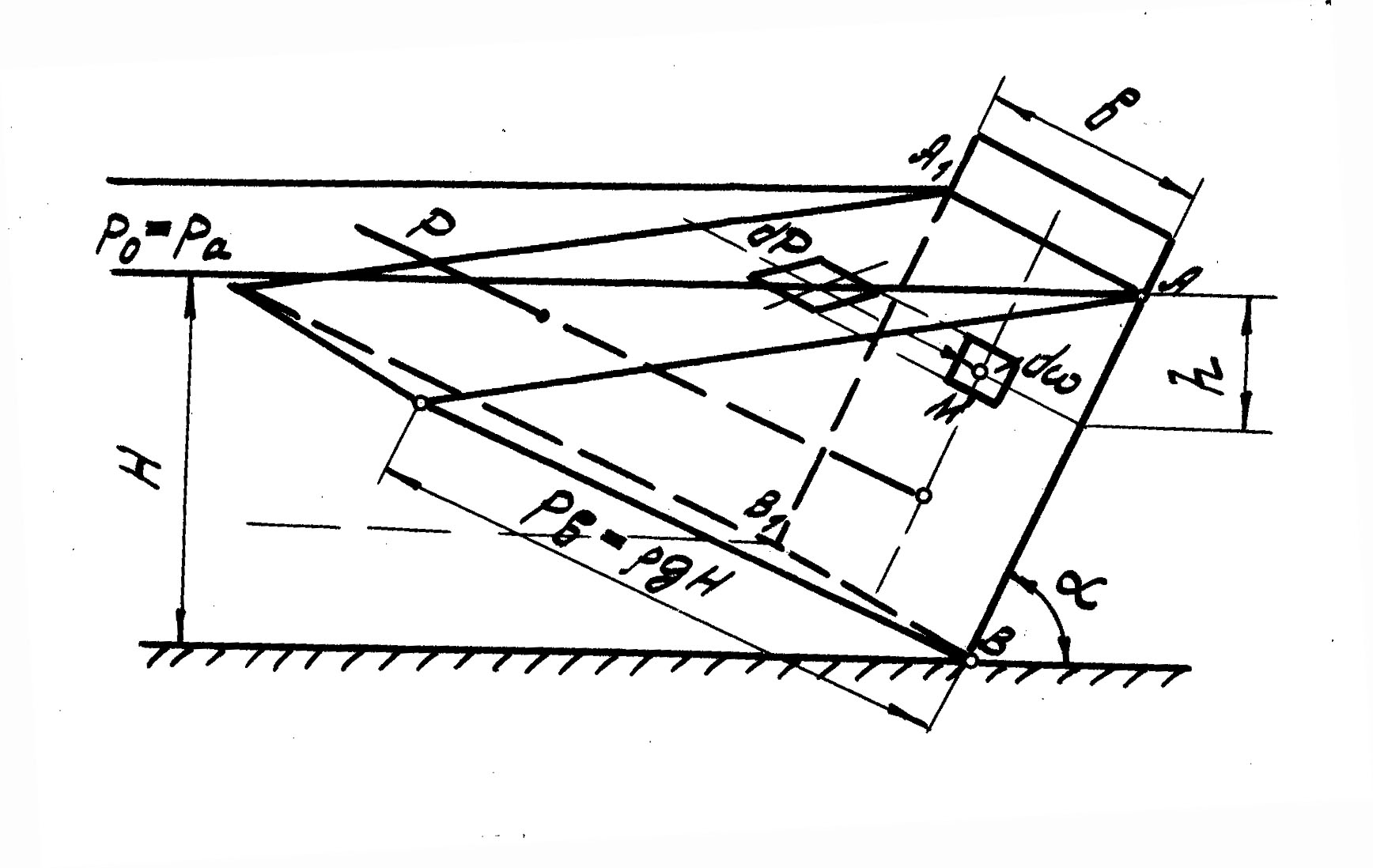Рис.8

Избыточное гидростатическое давление изменяется пропорцио­нально глубине погружения точки, для которой оно определяется, т.е. по закону прямой линии, поэтому соединим конец отрезка ВС (точку С ) с точкой А прямой. Треугольник ABC будет плоской эпюрой избыточного гидростатического давления. Распределение давления по всей стенке можно представить пространственной эпюрой в виде треугольной призмы ABCC₁B₁A_1. Каждая ордината этой призмы представляет в выбранном масштабе избыточное давление в соответствующей точке стенки, а весь объем призмы равен суммарному избыточному давлению жидкости на стенку.

Нетрудно доказать, что линия действия равнодействующей Р сил избыточного гидростатического давления нормальна к стенке ABB₁A₁, и проходит через центр тяжести пространственной эпюры, а следовательно, и через центр тяжести плоской эпюры, и встречается со стенкой в центре давления.

С этой целью выделим на плоскости ABB₁A₁ у точки М элементарную площадку . Избыточное гидростатическое давление в этой точке р = , где h − глубина погружения точки М. Если про­вести по периметру элементарной площадки нормали, то получим (в пределах эпюры давления) параллелепипед, объем которого р с некоторым приближением можно считать равным элементарной силе dP избыточного давления на площадку .

Если всю эпюру давления разбить на подобные элементарные па­раллелепипеды, то, очевидно, сумма их объемов будет равна объему всей эпюры, и следовательно, объем эпюры равен равнодействующей всех сил избыточного давления, а линия действия равнодействующей проходит через центр тяжести эпюры.

2.8. Давление жидкости на криволинейные (цилиндрические) (цилиндрические) поверхности

Выделим на некоторой цилиндрической поверхности АВ (рис. 9) элементарную площадку с центром тяжести, погруженным на глуби­ну h под свободную поверхность жидкости. Если давление на по­верхности жидкости равно р₀, то гидростатическое (абсолютное) давление в центре тяжести площадки составит

р=р_{0 +} .

Тогда dР − элементарная сила абсолютного гидростатического давления на площадку будет равна

dP = (p₀ + ) (2.33)

и направлена по нормали к ней, проведенной через центр тяжести.

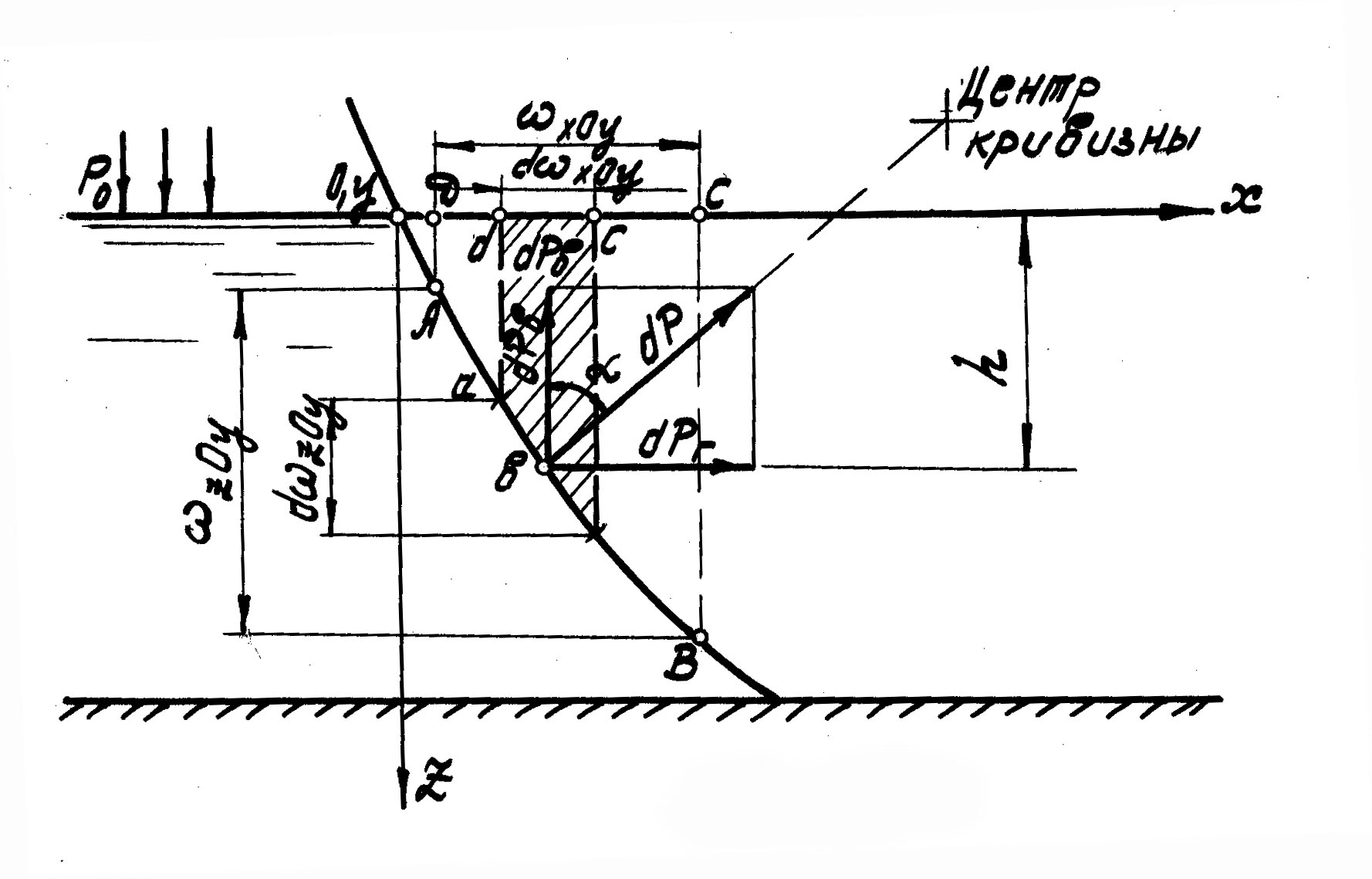
Рис.9

Разложим элементарную силу абсолютного гидростатического давления на вертикальную и горизонтальную составляющие, обозна­чив угол между элементарной силой dP и вертикалью через :

(2.34)

где ·cos = _xoy − площадь проекции на плоскость XOY; ·sin = _zoy − площадь проекции на плоскость ZOY.

С учетом приведенных выше равенств уравнение (2.34) можно записать в виде:

(2.35)

Если всю поверхность АВ разбить на ряд элементарных площа­док и для каждой из них определить значения dP_В и dP_Г, то вертикальную Р_В и горизонтальную Р_Г составляющие силы абсолютного гидростатического давления жидкости Р на цилиндрическую поверхность АВ можно найти суммированием всех элементарных сил dP_В и dP_Г или интегрированием уравнений (2.35):

(2.36)

. (2.37)

Первые интегралы в уравнениях (2.36) и (2.37) равны соответственно площадям проекций цилиндрической поверхности АВ на горизонтальную XOY и вертикальную ZOY плоскости, т.е.

, а .

Проведя вертикальные образующие через различные точки пара­метра элементарной площадки до координатной плоскости XOY, получим некоторый элементарный объем abcd, равный h· _xoy, т.е. объем, записанный под вторым интегралом в уравнении (2.36). Это уравнение теперь можно записать в виде

Р_В=р₀ + (объем ABCД). (2.38)

Следовательно, вертикальная составляющая силы абсолютного гидростатического давления равна сумме силы внешнего давления на горизонтальную проекцию цилиндрической поверхности АВ (пе­редающегося от воздействия внешней силы на поверхность жидкости) и веса жидкости в объеме АВСД, ограниченном цилиндрической по­верхностью АВ, вертикальными плоскостями АД и ВС свободной по­верхности жидкости, а также передней и задней вертикальными плоскостями.

Второй интеграл уравнения (2.37) равен статическому моменту площади проекции цилиндрической поверхности АВ на вертикальную плоскость ZOY относительно оси OY:

, (2.39)

где h_с − глубина погружения центра тяжести площади .

Из уравнений (2.37) и (2.39) находим

P_Г =(p₀+ _c)· . (2.40)

Это уравнение идентично уравнению (2.25). Следовательно, го­ризонтальная составляющая силы полного гидростатического давле­ния на цилиндрическую поверхность АВ равна силе абсолютного гидростатического давления, под воздействием которого находится вертикальная плоская стенка, равная по площади вертикальной про­екции цилиндрической поверхности АВ.

Складывая составляющие силы давления Р_В и Р_Г по правилу параллелограмма, получаем силу абсолютного гидростатического давления Р, действующую на цилиндрическую поверхность АВ:

. (2.41)

Построим эпюру абсолютного гидростатического давления на криволинейную поверхность АВ. Объем АВС₁Д₁ является эпюрой вертикальной составляющей абсолютного гидростатического давления на рассматриваемую поверхность АВ (рис. 10).

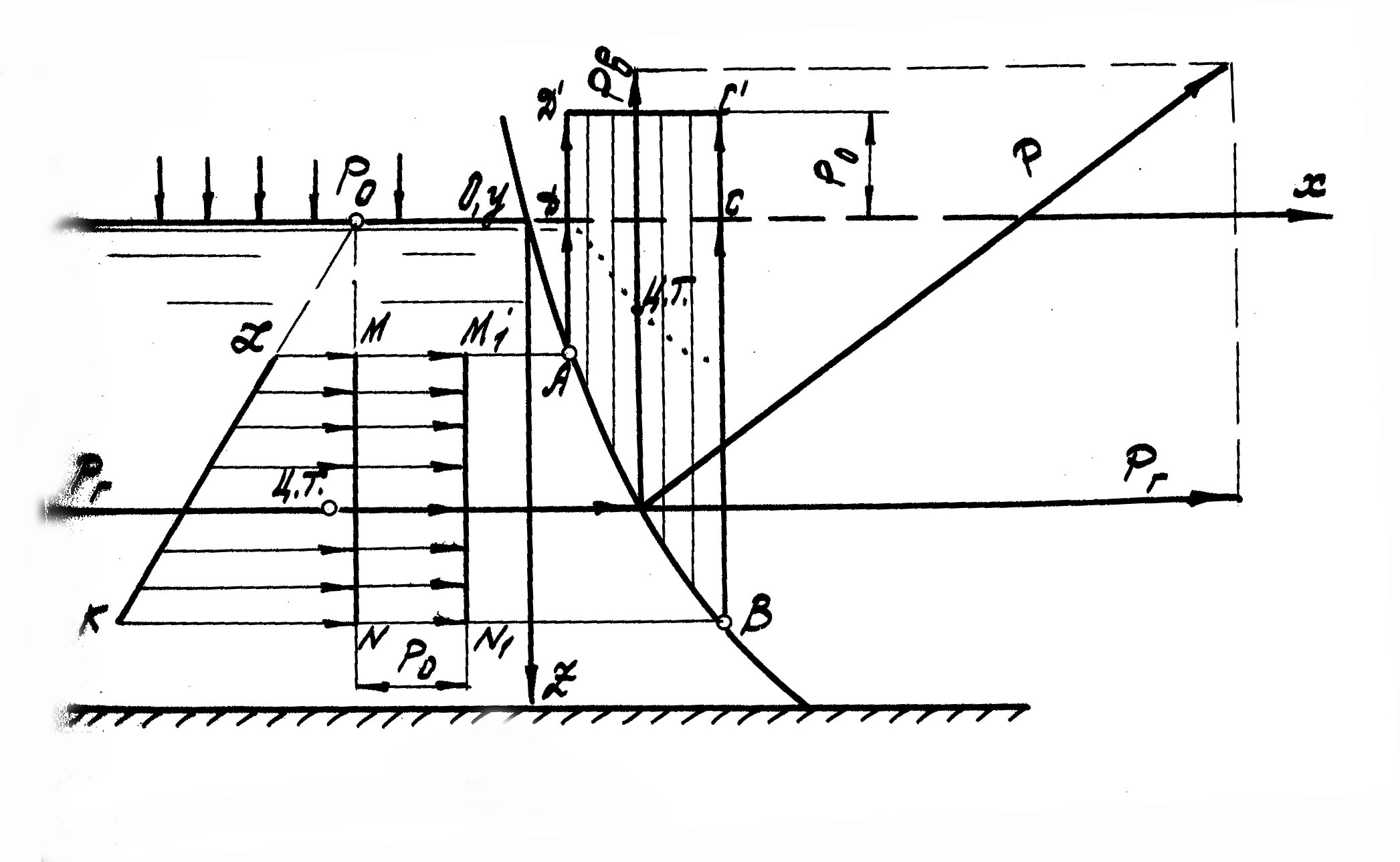
Рис.10

Эту эпюру можно рассматривать как состоящую из двух частей: эпюры АВСД, изобретающей избыточное (весовое) давление на площадь проекции поверхности АВ на плоскость XOY, и эпюры ДСС₁Д₁, характеризующей внешнее давление р₀. Сила давления Р_В, равная численно объему АВС₁Д₁, проходит через центр тяжести этого объема.

Эпюра горизонтальной составляющей абсолютного гидростатического давления на криволинейную поверхность АВ строится так же, как и для плоских стенок. В данном случае она представляется фигурой KZMN, которую можно рассматривать как состоящую из двух частей: эпюры KZM₁N₁, изображающей избыточное (весовое) давление жидкости, и эпюры MNN₁M₁, характеризующей внешнее давление р₀. Сила давления Р_T, равная объему эпюры KZM₁N₁, проходит через центр тяжести этого объема.