2.4. Полное (абсолютное) и манометрическое давление.

Пьезометрическая высота. Вакуум. Гидростатический напор

Если рассматривать гидростатическое давление жидкости на стенку сосуда, в который она налита, то в точке А (рис.4) это давление будет выражаться зависимостью (2.14). С внешней стороны на стенку сосуда действует атмосферное давление p_а. Следовательно, стенка сосуда будет испытывать давление, равное разности абсолютного гидростатического и атмосферного давлений. Превышение давления над атмосферным называется манометрическим или положительным избыточным гидростатическим давлением:

. (2.17)

Давление же p = p_м + p_а, т.е. гидравлическое давление с учетом атмосферного, называется абсолютным гидростатическим давлением.

Если сосуд открыт, как на рис.3, то давление на свободную поверхность жидкости равно атмосферному давлению p_а, т.е. p₀ = p_а. В этом случае манометрическое давление представляет собой весовое давление жидкости, равное

. (2.18)

Давление можно измерять также высотой столба, какой – либо жидкости (воды, ртути, спирта и т.д.), что видно из формулы (2.16).

Учитывая формулу (2.16), из уравнений (2.17) и (2.18) получим

. (2.19)

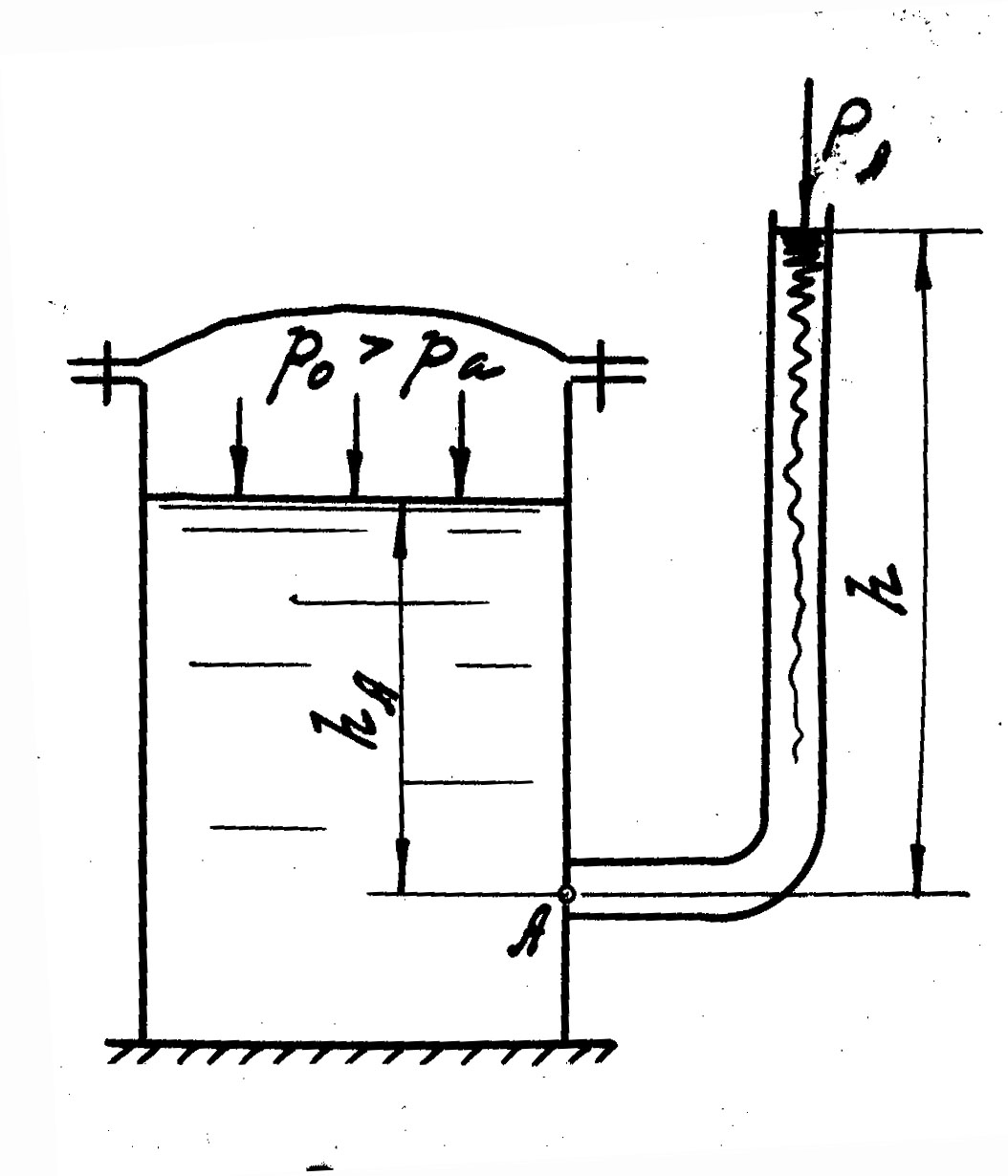
Рис.4

В выражении (2.19) переменными величинами являются лишь h и p_м, следовательно, манометрическое давление p_м в любой точке жидкости характеризуется только глубиной ее погружения или, иначе, глубина погружения любой точки характеризует манометрическое давление в ней.

Если в точке А к резервуару, наполненному жидкостью, присоединить открытую в атмосферу трубку (см.рис.4), то уровень жидкости в такой трубке установится на отметке, большей или меньшей

отметки уровня жидкости в резервуаре в зависимости от того, будет ли p₀ больше или меньше p_а. Такие трубки называют пьезометрами, или, в общем случае, жидкостными манометрами. Высоту h называют пьезометрической, или манометрической высотой. Пьезометрическая высота является мерой гидростатического давления в линейных единицах. Если атмосферное давление p_а (техническую атмосферу), равное 1кгс/м²=10тс/м²=9,81∙10⁴Н/м², выразить пьезометрической высотой h (в метрах водяного столба), то получим

м вод. ст.

Следовательно, одна техническая атмосфера измеряется высотой столба воды 10 м.

Пользуясь пьезометром, можно определить давление в любой точке жидкости путем отсчета высоты столба жидкости.

Если абсолютное гидростатическое давление в какой-либо точке жидкости (рис.5) меньше атмосферного (p<p_а),то манометрическое давление в ней будет отрицательным. Например, если в точке А (рис.5) p_А/ =6 м вод.ст., то получаем

м вод. ст. = -0,4ат.

В буквальном выражении можно записать

, где .

Отсюда – вакуумметрическая высота,

где p₀/ +h_А=p_А/ −высота, отвечающая абсолютному гидростатическому давлению в точке А:

м вод. ст.

Знак минус указывает, что давление в рассматриваемом баллоне А меньше атмосферного на 0,4 атм, а жидкость в ней сжата давлением 0,6 атм, следовательно, не испытывает растягивающих напряжений.

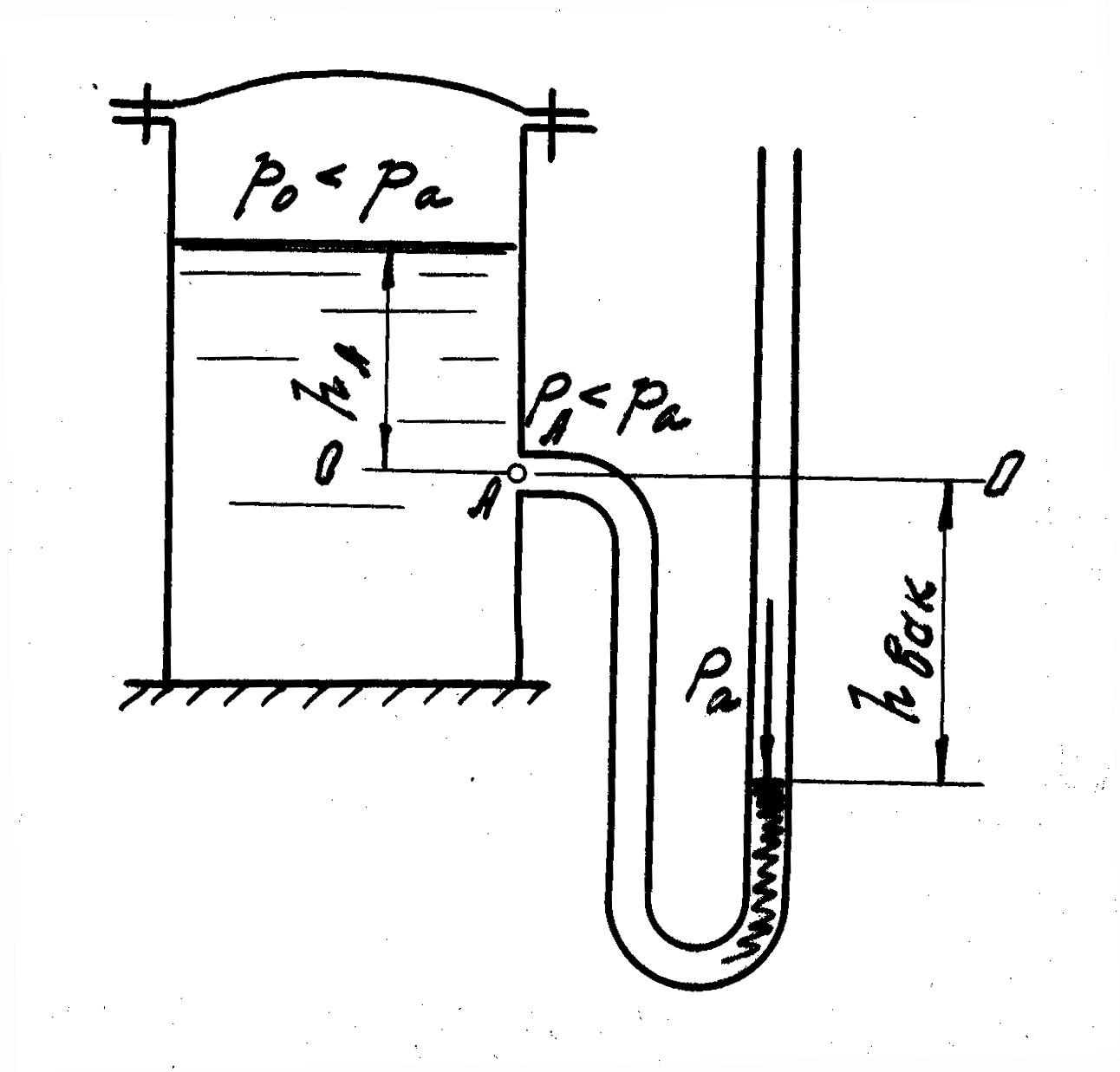
Рис.5

Недостаток абсолютного давления до атмосферного называют вакуумом (от латинского vacuum − разрежение). Высоту столба жидкости, измеряющую вакуум, называют вакуумной высотой и обозначают:

. (2.20)

Из выражения (2.20) следует, что вакуум может меняться в пределах от 10 м вод. ст. (1ат) до нуля.

Приборы для измерения вакуума называют вакуумметрами или обратными пьезометрами.

Рассмотрим жидкость в закрытом резервуаре с давлением на свободной поверхности p₀ (рис. 6). Выберем в этом резервуаре две произвольные точки А и В и присоединим к каждой из них по пьезометру. Для сопоставления величин выберем плоскость сравнения (линия 0-0). Обозначим координаты (отметки) точек А и В по отношению к плоскости сравнения 0-0 через z_А и z_В. Если избыточное гидростатическое давление в этих точках соответственно p_А и p_В, то пьезометрические высоты в пьезометрах, подключенных к точкам А и В соответственно будут равны p_А/ и p_В/ .

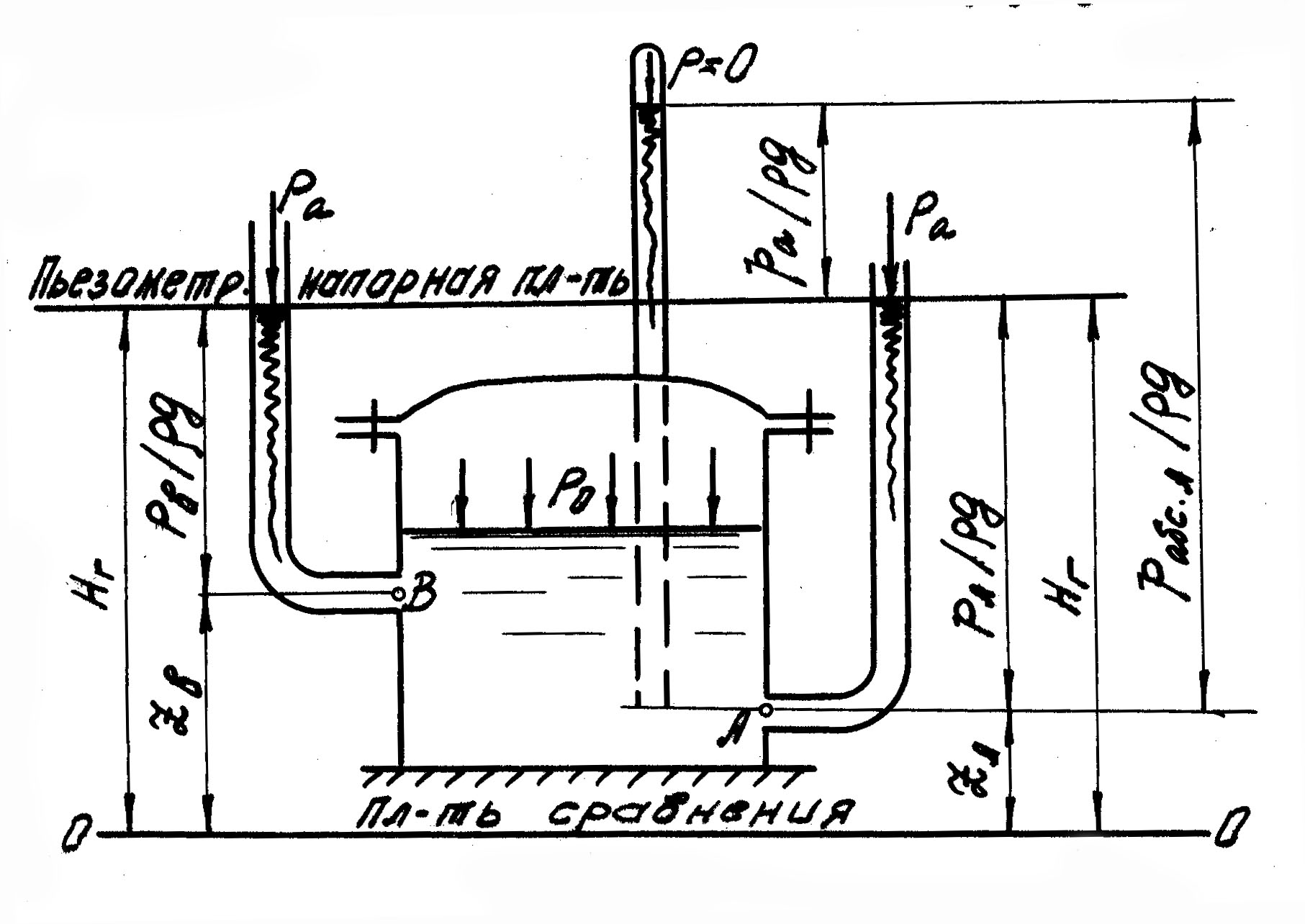
Рис.6

Суммы высот Z_А+p_А/ или Z_В=p_В/ называются гидростатическим напором в данной точке жидкости относительно выбранной плоскости сравнения 0–0. Согласно уравнению (2.21), эти суммы равны между собой. Следовательно, для данного объема жидкости гидростатический напор относительно выбранной плоскости сравнения есть величина постоянная, т.е.

. (2.21)

Если же к точкам А и В подсоединить запаянные сверху трубки, из которых откачан весь воздух, то жидкость в этих трубках поднимается выше, чем в пьезометрах на высоту p_а/ , отвечающую атмосферному давлению.

Высота подъема уровня жидкости в запаянной трубке будет выражать абсолютное гидростатическое давление в точке, к которой трубка присоединена.