Разделив переменные
и
проинтегрировав это уравнение в пределах
для
от
до
(где
–радиус колодца) и соответственно для
от
до
,
т. е. пренебрегая участком высачивания
,
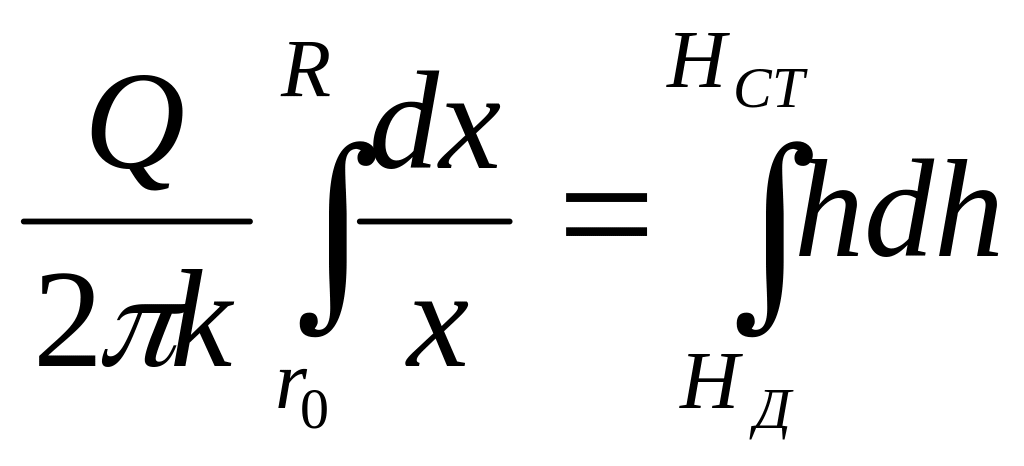получим следующее выражение:
,
(9.15)
известное под названием формулы Дюпюи.
Расход, т.е. искомый дебит колодца, определяется выражением
.
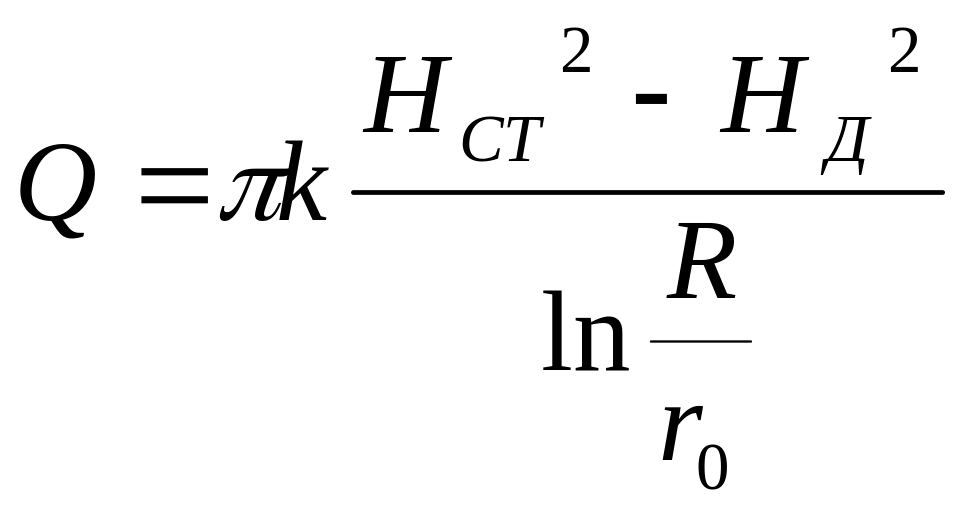(9.16)
Для
определения формы кривой депрессии
необходимо, задаваясь различными
значениями х
(вместо
R),
определить
из уравнения (9.15)
соответствующие им значения h
( вместо
)
и по точкам построить
кривую, которая представляет собой
параболу в координатах
,
.
Опытными проверками установлено, что расход, определяемый по формуле Дюпюи, совпадает с действительным расходом, не смотря на неучет промежутка высачивания; положение же кривой депрессии при этом, естественно, определяется лишь приближенно.
9.5. Напорное движение грунтовых вод
Рассмотрим случай, когда водоносный пласт располагается между двумя водонепроницаемыми слоями и находится под избы точным давлением.
Если в таком пласте заложить колодец (скважину) и из него откачать воду, то толщина водоносного слоя, в отличие от случая, рассмотренного в предыдущем параграфе, не изменится, а изменится давление в пласте, убывая по направлению к колодцу. Отметим, что в тех случаях, когда глубина колодца меньше напора, соответствующего давлению в пласте до начала откачки, колодец будет фонтанировать и вода самоизливаться на поверхность земли.
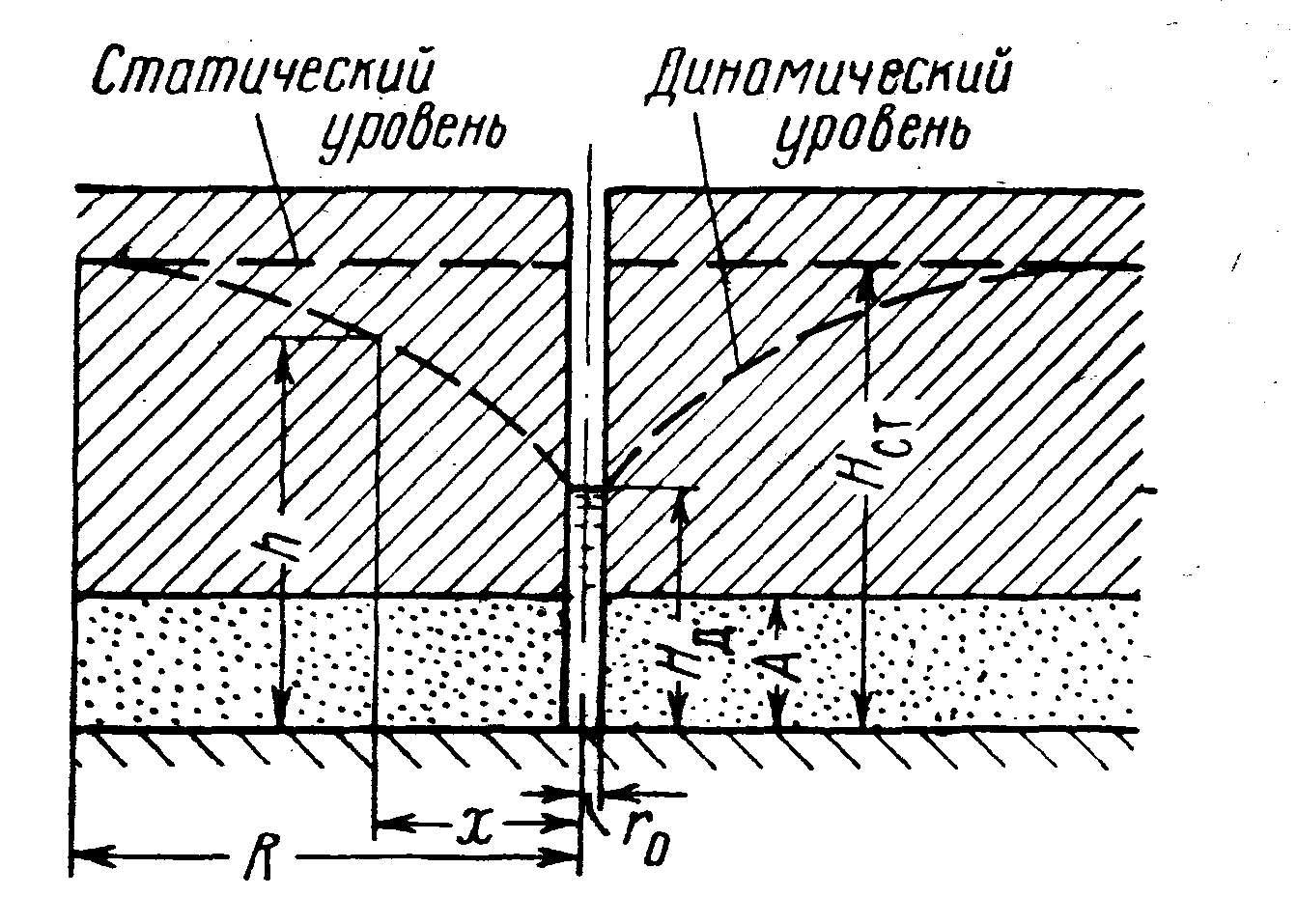
Рис.7
Подобного рода колодцы (скважины) обычно называют артезианскими. Пусть (рис.7). Толщина водоносного слоя будет А, напор в пласте на расстоянии R (радиус влияния) от оси колодца и высота уровня в колодце после откачки . Тогда, по аналогии с предыдущим, расход воды, проходящей через цилиндрическое сечение водоносного пласта, взятое на расстоянии х от оси колодца, будет
,
где
i
–по-прежнему
гидравлический уклон. Подставляя сюда
вместо i
его
значение,
равное
,
разделяя переменные и интегрируя
выражение
в пределах для х от до и для h от до , получаем
.
При этом дебит артезианского колодца при напорной фильтрации определяется выражением
.
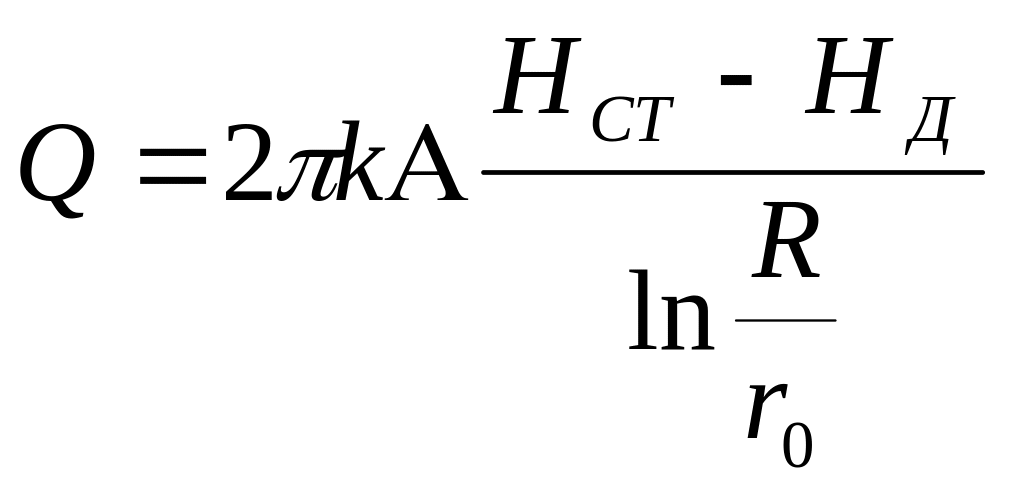(9.17)
Так как последнее уравнение дает прямую линейную зависимость дебита от понижения уровня воды в колодце, для характеристики напорного водоносного пласта иногда вводят также понятие о так называемом удельном дебите, понимая под последним величину дебита при понижении уровня воды в колодце на 1 м.
Удельный дебит обычно определяется опытным путем на основании пробных откачек:
.
(9.18)