9.3. Определение коэффициента фильтрации

Во все формулы предыдущего параграфа, определяющие скорость фильтрации, входит коэффициент фильтрации , имеющий исключительно большое значение во всех фильтрационных расчетах. Величина этого коэффициента обычно определяется опытным путем на установке, подобной изображенной на рис.4. Установку загружают опытным образцом грунта и, измеряя расход фильтрации и потерю напора, путем непосредственного вычисления по формуле (9.3) находят коэффициент фильтрации:

.

Для теоретического определения коэффициента фильтрации различными авторами предложен ряд эмпирических расчетных формул. Некоторые из них, применимые только для песчаных грунтов, приводятся ниже. В этих формулах k –коэффициент фильтрации, см/с; –абсолютная вязкость жидкости, П.

Одной из таких формул является формула Газена

, (9.11)

где d_e –эффективный диаметр, см, определяемый по указанному выше методу; с –некоторый коэффициент, учитывающий пористость грунта и имеющий следующие значения: для очень плотных песков с=0,8, для песков средней пористости с=1,55, для песков, составленных из округленных частиц, почти одинакового диаметра.

Для воды формула Газена может быть представлена в следующем виде:

, (9.12)

где t –температура воды в С.

Следует иметь в виду, что формула Газена применима для грунтов с эффективным диаметром от 0,1 до 3 мм.

Приведем формулу Слихтера

, (9.13)

где –коэффициент, зависящий от пористости т и просвета фиктивного грунта и равный .

Под эффективным диаметром d_e в этой формуле, в отличии от формулы Газена, понимают средний весовой диаметр частиц, определенный по весовой кривой, т. е. такой диаметр, который весовые количества частиц мельче и крупнее его поровну.

Для воды при t = 10° С, когда = 0,01333 П, формула Слихтера принимает вид

. (9.14)

При приближенных расчетах можно принимать следующие средние значения коэффициента фильтрации , см/с:

для грунтов очень большой проницаемости (средний и крупный гравий с примесью очень крупного песка) – 0,5-1;

грунтов большой проницаемости (крупный песок с мелким гравием) –0,2-0,5;

грунтов средней проницаемости (среднезернистый песок, чистый мелкий песок) – 0,1-0,2;

грунтов малой проницаемости (слабоглинистый песок, очень мелкий песок) – 0,01-0,02.

Для грунтов очень малой проницаемости Н. Н. Павловский рекомендует следующие значения , см/с:

для песчаных грунтов с некоторой примесью глины – 0,006-0,007;

песчано-глинистых грунтов – 0,003-0,004;

проницаемых глин – 0,001.

9.4. Безнапорное движение грунтовых вод

В качестве примера безнапорного движения грунтовых вод paссмотрим откачку воды из колодца или скважины, заложенной в водоносном пласте с горизонтальным непроницаемым подстилающим слоем. До начала откачки грунтовые воды в пласте находятся в покое и поверхность их горизонтальна. Если откачивать воду из колодца, в водоносном слое начнется движение грунтовых вод к колодцу.

При этом уровень воды в колодце понизится. Одновременно произойдет понижение уровня грунтовых вод в пласте; это понижение будет наибольшим у стенок колодца, постепенно убывая по мере отдаления от него (рис.5). Чем интенсивнее будет производиться откачка, тем ниже будет располагаться уровень воды и колодце и тем больше будет его дебит (расход).

Уровень стояния воды в колодце до начала откачки , одинаковый с уровнем во всем водоносном пласте, обычно называют статическим. Уровень , устанавливающийся в колодце в процессе откачки, носит название динамического, а сечение открытой поверхности уровня воды в пласте вертикальной плоскостью, проходящей через ось колодца, называется кривой депрессии, или кривой падения уровня (схематически показана пунктиром на рис.6).

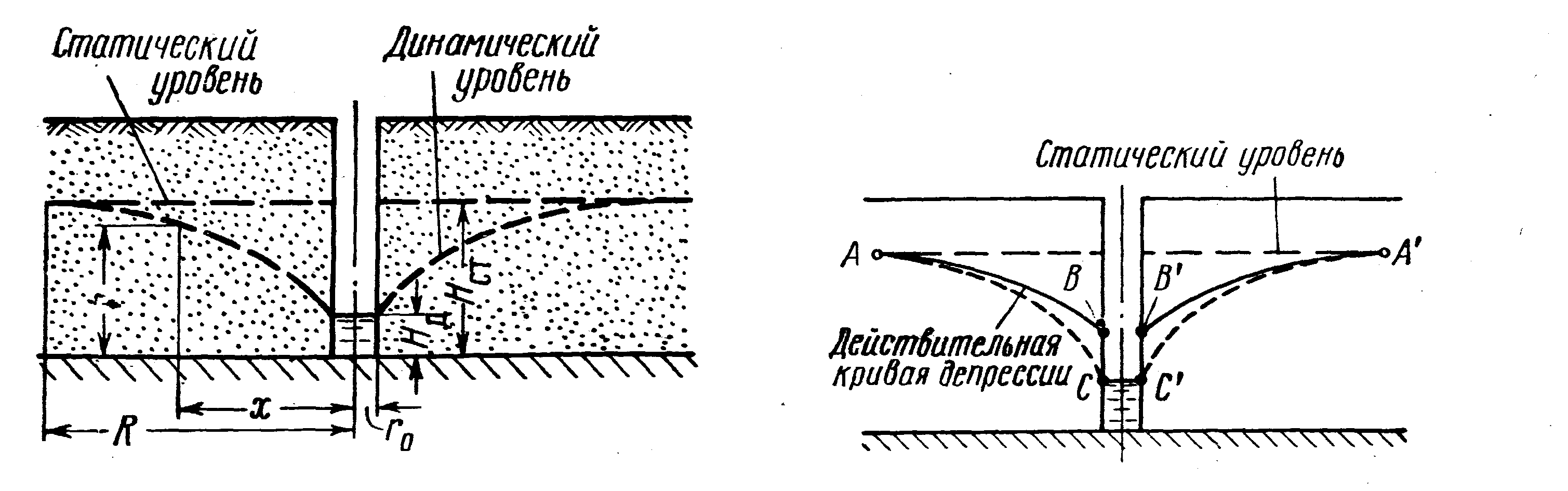
Рис.5 Рис.6

В действительности кривая дисперсии выклинивается на стенках колодца несколько выше поверхности воды в нем, образуя так называемый «промежуток высачивания» (рис.6). На этом промежутке ВС вода будет сочиться в атмосферу и стекать в колодец вдоль его стенок. Действительная кривая депрессии изображается кривой АВСС'В'A'.

При откачке из одиночного колодца (скважины) снижение уровня, вызываемое откачкой, на некотором расстоянии от оси колодца практически перестает быть заметным; это расстояние называется радиусом дренирования, или радиусом влияния колодца (скважины). При предварительных расчетах его можно принимать равным для песчаных грунтов от 350 до 500 м, для крупнозернистых грунтов –700 м.

Предполагая этот радиус R известным, зная толщину (мощность) водоносного слоя и задаваясь динамическим уровнем в колодце, можно определить расход воды в колодце и установить приближенную форму депрессионной кривой.

Для этого рассмотрим движение воды через некоторое цилиндрическое сечение водоносного слоя на расстоянии х от оси колодца. Если глубина воды в этом сечении , площадь сечения будет равна

.

При этом расход фильтрации

,

где w –скорость фильтрации, определяемая, как обычно, по формуле Дарси (9.4),

.

Подставляя это значение скорости в выражение для расхода, получаем

.

Гидравлический уклон в этом выражении можно заменить через отношение бесконечно малой потери напора, т. е. падения уровня dh, бесконечно малому пути в радиальном направлении dx.

.

Тогда .