9.2. Основные законы фильтрации

Первые исследования движения жидкости в пористых телах были проведены в середине ХIХ в. французским гидравликом Дарси. В своих опытах Дарси применял прибор (рис.4), состоящий из вертикального цилиндрического сосуда, заполненного слоем песка, через который при постоянной разности напора пропускалась вода.

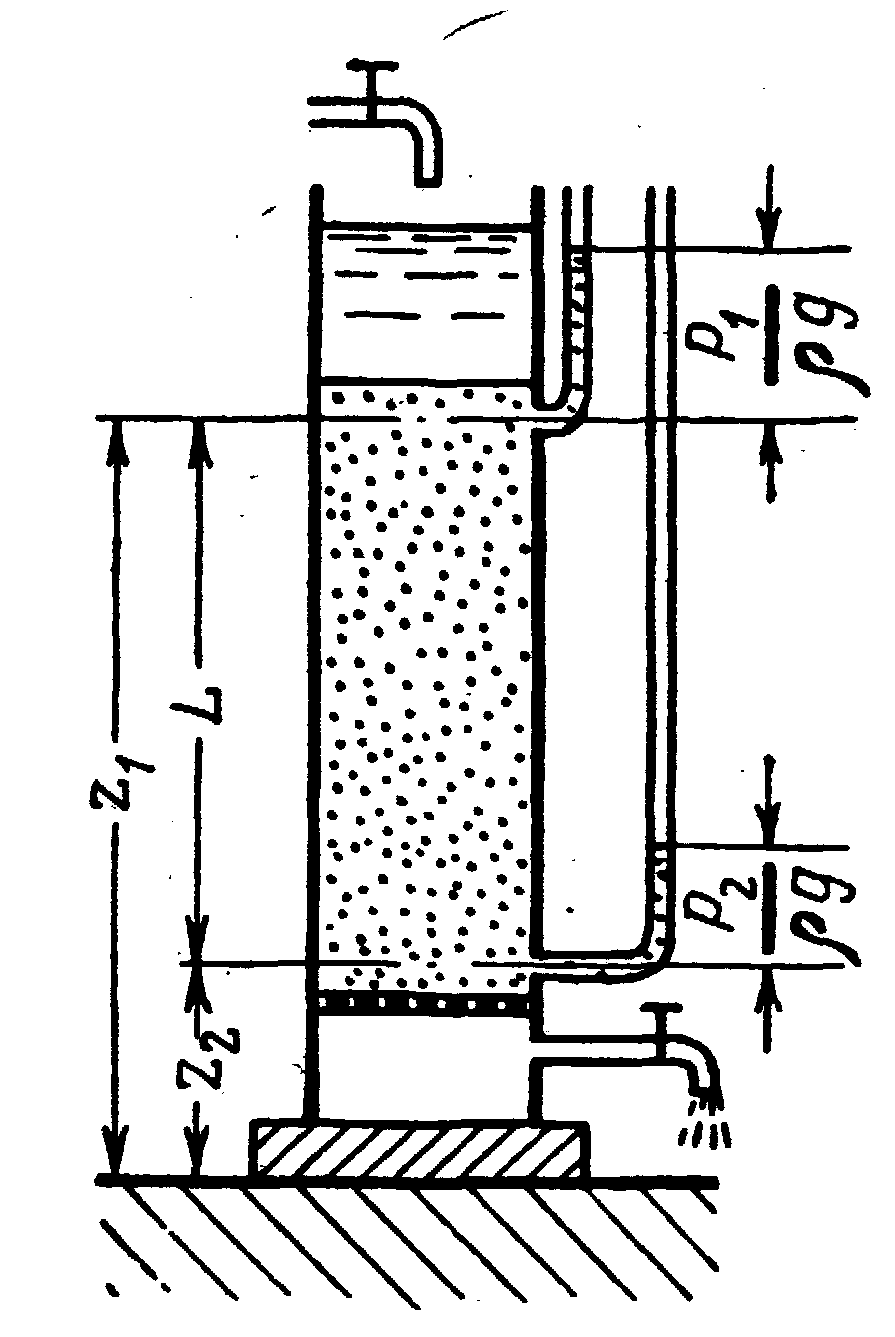
Рис.4

Определяя при помощи пьезометров давления в различных по высоте сечениях фильтрующего слоя, изменяя толщину этого слоя и состав песка и измеряя расход фильтруемом воды, Дарси установил основной закон фильтрации, которому подчиняются различные несжимаемые жидкости (вода, нефть) при своем движении через грунт. Этот закон носит название закона Дарси и имеет следующее математическое выражение:

, (9.3)

где Q –расход жидкости при фильтрации, –площадь фильтрации, под которой понимают полное сечение всего фильтрующего слоя, включая как сам грунт, так и поры между отдельными его частицами (для рассматриваемого случая есть площадь поперечного сечения сосуда); h –потеря напора, равная

и определяемая по разности показаний пьезометров (здесь –плотность жидкости); L –толщина слоя грунта в направлении фильтрации; –коэффициент фильтрации, характеризующий одновременно как фильтрационные свойства пористой среды –грунта, так и физические свойства фильтрующейся жидкости.

Уравнение (9.3) можно представить также в более простой форме

, (9.4)

где

есть средняя в сечении фильтрующего слоя скорость фильтрации, а

,

i –гидравлический уклон, представляющий собой падение напора на единицу длины.Из этой формулы следует, что коэффициент фильтрации имеет размерность

,

т. е. размерность скорости (так как гидравлический уклон i есть величина безразмерная). Обычно он измеряется в см/с. Отсюда видно также, что при , т. е. физически коэффициент фильтрации представляет собой скорость фильтрации при единичном уклоне.

Дарси проводил свои опыты с водой. В дальнейшем при исследовании фильтрации других жидкостей было установлено, что скорость фильтрации обратно пропорциональна вязкости. В связи с этим вязкость жидкости была выделена в отдельный параметр.

В то же время скорость фильтрации стали определять не через перепад напора h, а исходя из разности давлений , соответствующей этому перепаду ( ). Таким образом,

, (9.5)

где –коэффициент проницаемости, характеризующий фильтра­ционные свойства самого грунта; –абсолютная вязкость жидкости.

Коэффициент проницаемости связан с коэффициентом фильтрации соотношением

, (9.6)

легко получаемым из сопоставления формул (9.4) и (9.5).

Размерность коэффициента проницаемости

,

т. е. размерность площади.

В международной системе единиц коэффициент проницаемости измеряется в м²; в физической системе единиц –в см². За практическую же единицу коэффициента проницаемости принимают проницаемость грунта, который при площади фильтрации толщине слоя фильтрации L=1см, абсолютной вязкости фильтрующейся жидкости г/см·с (сП –сантипуаз) и потере давления (соответствующей потере напора h) = 1 кгс/см² (ат) пропускает расход жидкости Q = 1 см³/с Такая единица проницаемости называется дарси (обозначается Д); единица, равная 0,001 дарси носит название миллидарси (мД):

.

Закон Дарси часто называют законом ламинарной фильтрации, так как согласно этому закону расход и скорость фильтрации линейно зависят от потери напора, что является первым признаком ламинарного режима, что отмечалось ранее при рассмотрении движения жидкости в трубопроводах. В большинстве случаев движение жидкости в пористых телах действительно происходит с весьма малыми скоростями, и сечения отдельных пор грунта также весьма малы, что делает возможным уподобить фильтрацию ламинарному движению в тонких неправильной формы капиллярных трубках. Поэтому закон Дарси, хорошо согласующийся с действительностью, является основным законом фильтрации и обычно используется при решении различного рода практических задач в этой области.

В отдельных случаях, когда движение жидкости в грунте характеризуется значительными скоростями, что может иметь место в крупнотрещиноватых и крупнопористых породах (например, в галечниках и скальных породах), наблюдается переход к турбулентному режиму. Закон Дарси здесь нарушается, и формулы (9.3) и (9.4) неприменимы.

Закон Дарси неприменим также и при фильтрации в весьма мелких зернистых, глинистых грунтах с очень малыми скоростями, когда начинают заметно сказываться капиллярные силы поверхностного натяжения. Эти случаи не имеют, однако, особенного практического значения, так как даже при весьма малых размерах частиц грунта, диаметром всего лишь около 0,05мм, и небольших скоростях филь­трации закон Дарси все еще оказывается справедливым.

Граница перехода от ламинарного режима к турбулентному устанавливается по критическому значению числа Рейнольдса Re, для определения которого при фильтрации предложен ряд эмпирических формул. Так, по Н. Н. Павловскому.

, (9.7)

по В. Н. Щелкачеву

, (9.8)

где –кинематическая вязкость жидкости, а остальные обозначения те же, что и ранее.

Критическое значение числа Рейнольдса при его определении по формуле Павловского лежит в интервале: .

а по формуле Щелкачева .

Для определения скорости фильтрации при турбулентном режиме применяются следующие формулы: формула Краснопольского (в форме, приданной ей Щелкачевым)

, (9.9)

где плотность жидкости, и формула Смрекера

(9.10)

где с –коэффициент пропорциональности, определяемый опытным путем; –показатель степени, изменяющийся в зависимости от вида грунта в пределах от ¹/₃ до 1.