8.4. Движение жидкости в самотечных трубопроводах

К безнапорным (самотечным) трубопроводам относятся канализационные трубы, водосточные каналы (ливнеспуски), самотечные нефтепроводные и водопроводные трубы и т.д.

Наиболее распространенными формами сечений безнапорных трубопроводов являются: круглое (рис.5), овоидальное (рис.5) и лотковое (рис.5). Эти сечения характеризуются интересной гидравлической особенностью: наибольший расход и наибольшая скорость в них имеют место не при полном, а лишь при частичном наполнении.

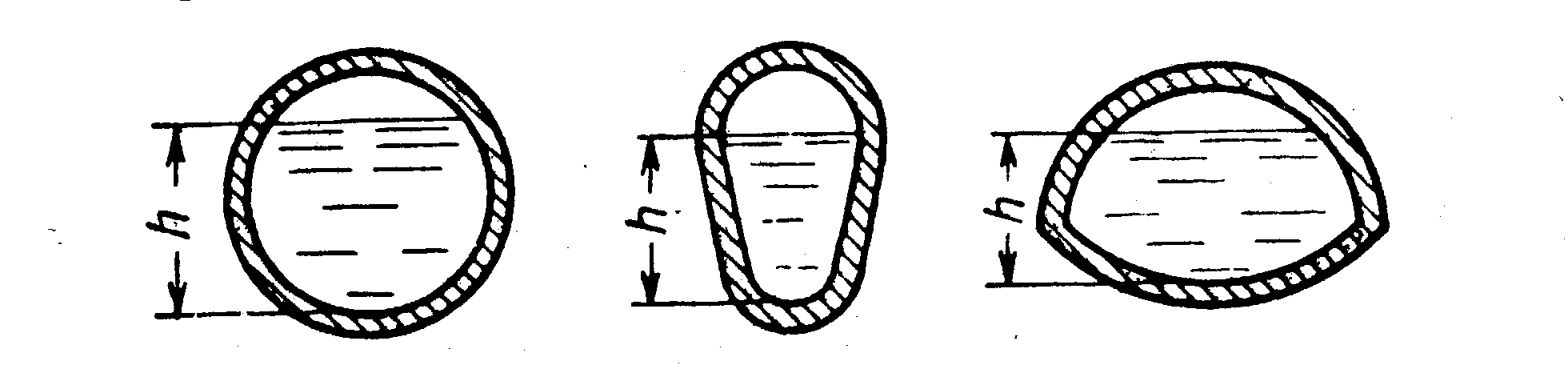
Рис.5

Объясняется это тем, что при заполнении верхней части подобных сечений смоченный периметр растет быстрее, чем площадь, и поэтому начинает уменьшаться гидравлический радиус, что приводит одновременно к уменьшению скорости и расхода.

Гидравлические расчеты безнапорных трубопроводов выполняются аналогично расчетам открытых каналов, что естественно, поскольку безнапорный трубопровод представляет собой по существу также открытый канал; отличием трубопроводов от каналов в гидравлическом смысле является только отмеченное выше уменьшение гидравлического радиуса трубопроводов при заполнении его верхней части, в то время как гидравлический радиус каналом все время возрастает с увеличением наполнения.

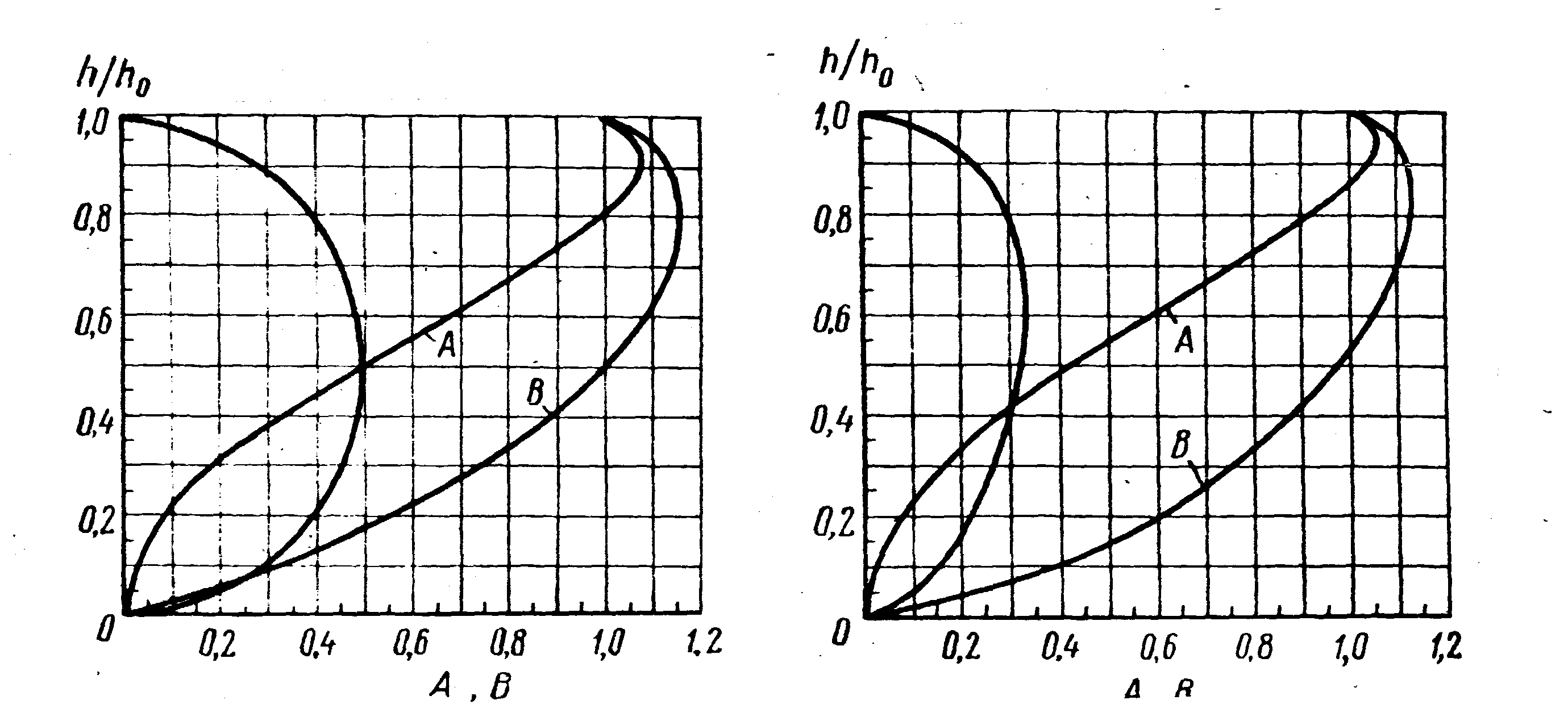
Рис.6 Рис.7

Для упрощения расчетов значения характеристик трубопроводом (площади сечения, гидравлического радиуса и величин и зависящие от глубины наполнения, могут быть вычислены для определенных форм сечения заранее.

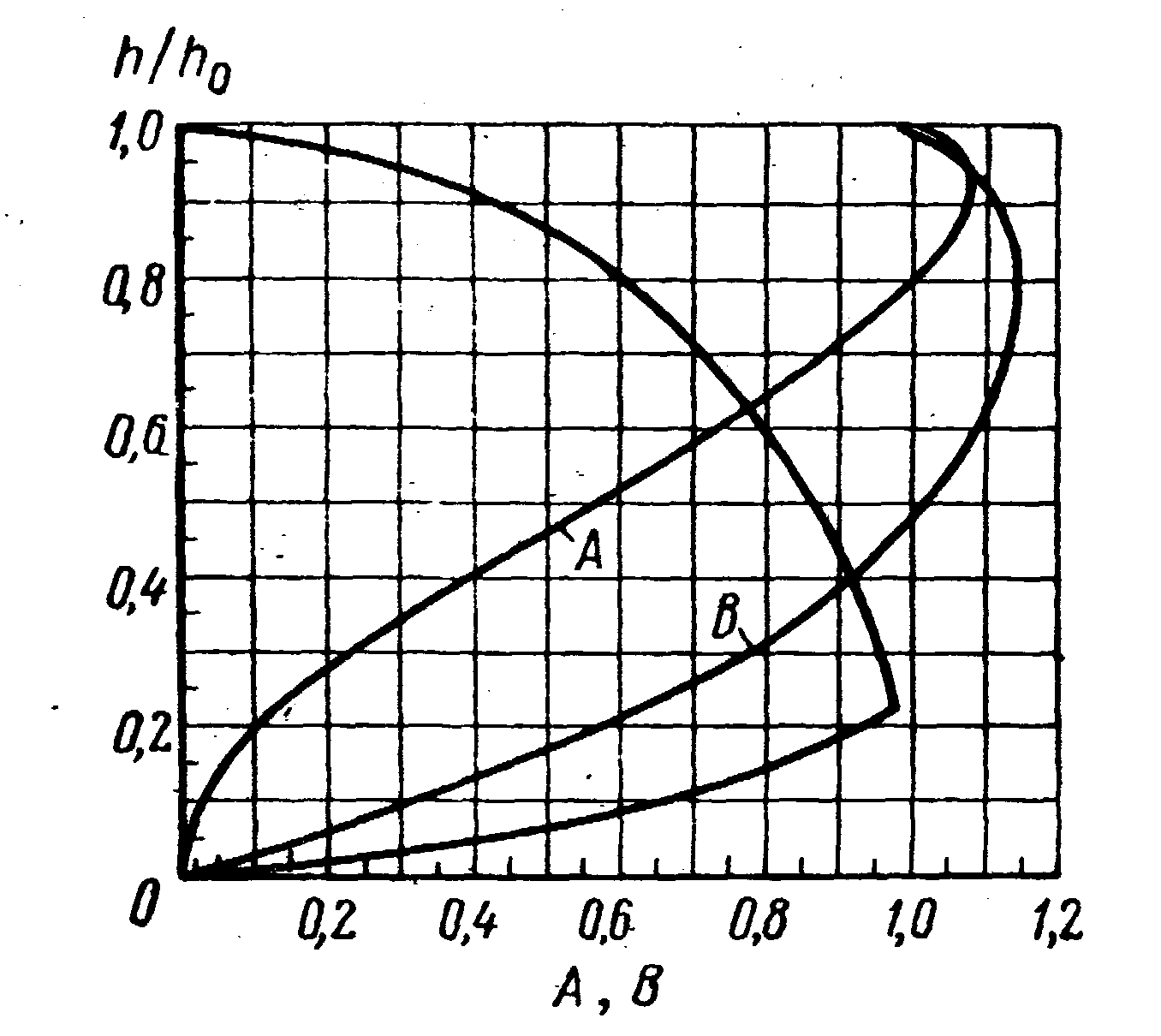
Рис.8

Если обозначить через W₀ и значения модуля скорости и модуля расхода при полном наполнении h₀трубопровода, а теми же буквами без индекса –их значения при некотором частичном наполнении h, можно вычислить значения отношений

в зависимости от ; получающиеся при этом зависимости для трубопроводов круглого, оваидального и лоткового сечений представлены в виде графиков на рис.6, 7, 8. Пользуясь этими графиками, значения скорости и расхода Q при частичном наполнении можно находить по формулам

, (8.18)

. (8.19)

8.5. Безнапорное движение при ламинарном режиме

На практике, например при сливе весьма вязких нефтей и нефтепродуктов и их течении в открытых лотках и самотечных трубах, при решении некоторых задач в области химического и нефтезаводского аппаратостроения, иногда приходится встречаться с ламинарным безнапорным движением жидкости.

В этом случае оказывается возможным определить теоретическим путем потери напора (подобно тому, как при ламинарном движении в напорных трубах) и получать расчетные зависимости для расхода. Не приводя здесь соответствующих решений, математически обычно весьма сложных и громоздких, ограничимся лишь сводкой некоторых расчетных формул для каналов наиболее часто применяемых форм поперечных сечении. По И.А.Чарному, для канала прямоугольного сечения при глубине потока h и ширине b расход жидкости может быть подсчитан по формуле

(8.20)