7.7. Гидравлический расчет сложных трубопроводов

Сложные трубопроводы подробно рассматриваются в специальных курсах.

Ниже приводятся основы гидравлического расчета параллельно разветвленного трубопровода и трубопровода с непрерывной раздачей расхода по пути.

Параллельно разветвленный трубопровод

На рис.9 приведена схема сложного трубопровода, состоящего из ветвей различной длины и диаметра, соединенных параллельно.

Цель гидравлического расчета заключается в определении расходов в каждой ветви и потерь напора Н на пути от А до В.

В точках А и В гидростатические напоры являются общими для каждой из n ветви, поэтому потеря напора для любой из ветвей будет одинаковой и равной:

.

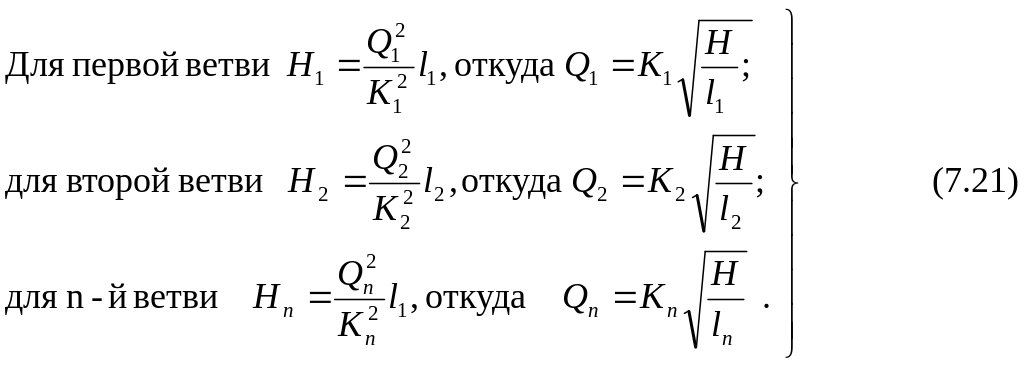
Так как система состоит из n уравнений, в которых (n+1) неизвестных, а именно n расходов ( ) и потеря напора Н, то для решения задачи требуется еще одно уравнение. Им может служить уравнение, полученное из условия неразрывности, а именно:

(7.22)

При совместном решении системы уравнений (7.21) и (7.22) определяются потери напора Н и расходы в ветвях . Задача решается в такой последовательности. После совместного решения уравнений (7.21), найдем

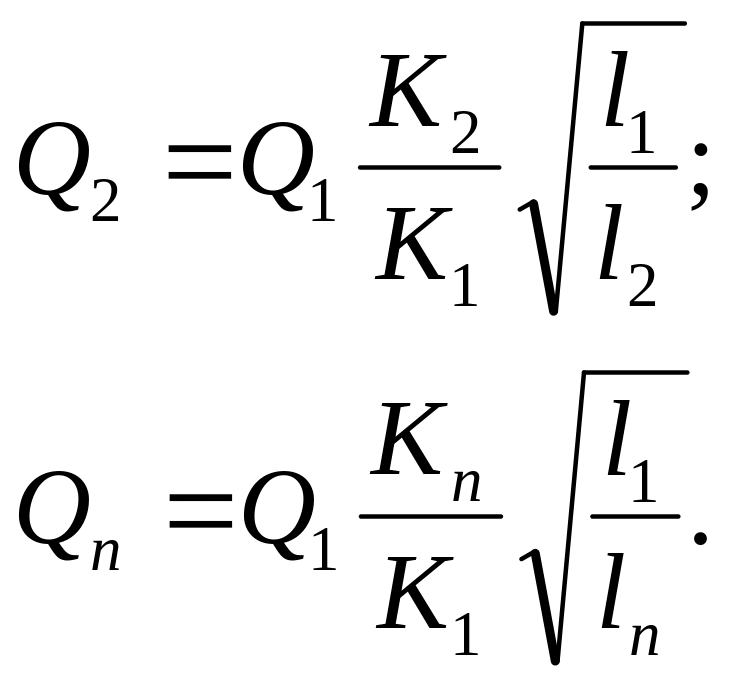
Затем, пользуясь уравнением (7.22), будем иметь

,

откуда

.

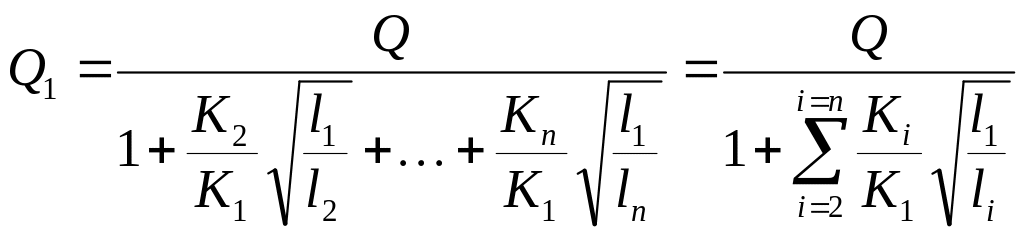Далее определяем .

Потерю напора Н можно определить по формуле

.

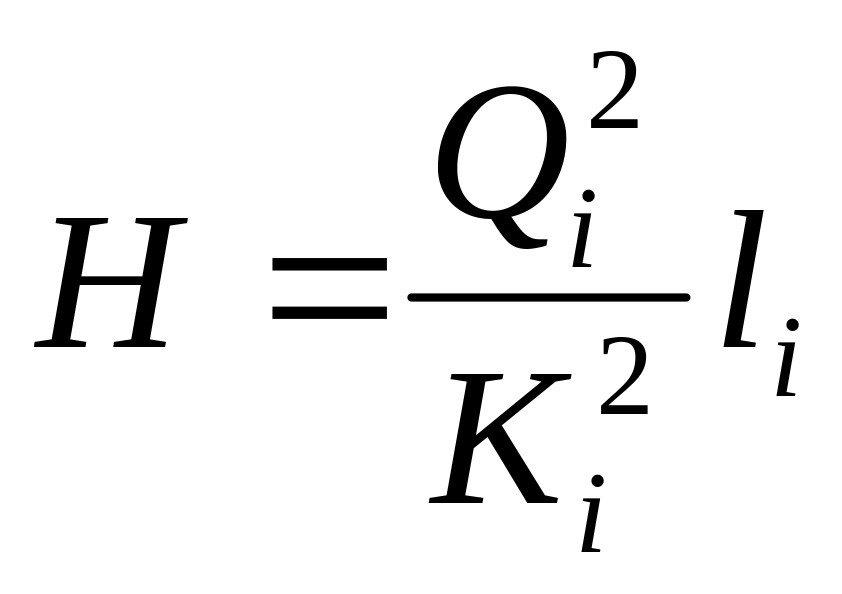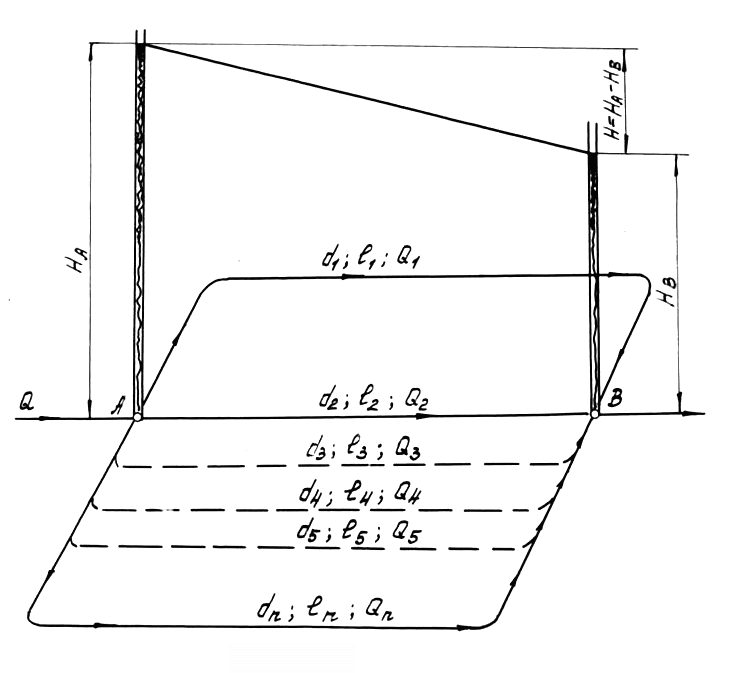
Рис.9

7.8. Гидравлический расчет простого длинного трубопровода

с непрерывной равномерной раздачей расхода по пути

Пусть на участке А–В (рис.10) через продольную щель трубопровода происходит непрерывный сброс жидкости так, что расход , который проходит к узлу А, постепенно уменьшается по пути к узлу В до величины транзитного расхода . Под транзитным расходом понимается расход, проходящий без изменения про участку А–В и предназначенный для использования на участке, расположенном ниже по течению.

Допустим, что сбросной расход на участке А–В распределяется равномерно, т.е. .

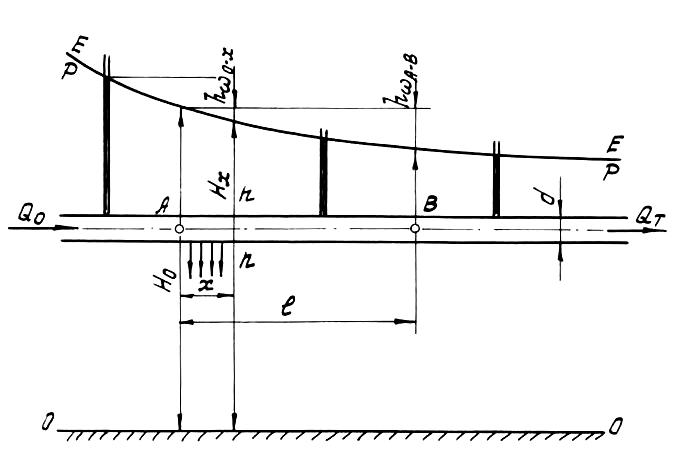
Рис.10

Определяем расход в створе n-n трубы на расстоянии Х от узла А

,

где –сбросной расход на участке от узла А до створа n-n.

Гидравлический уклон в сечении n-n будет

,

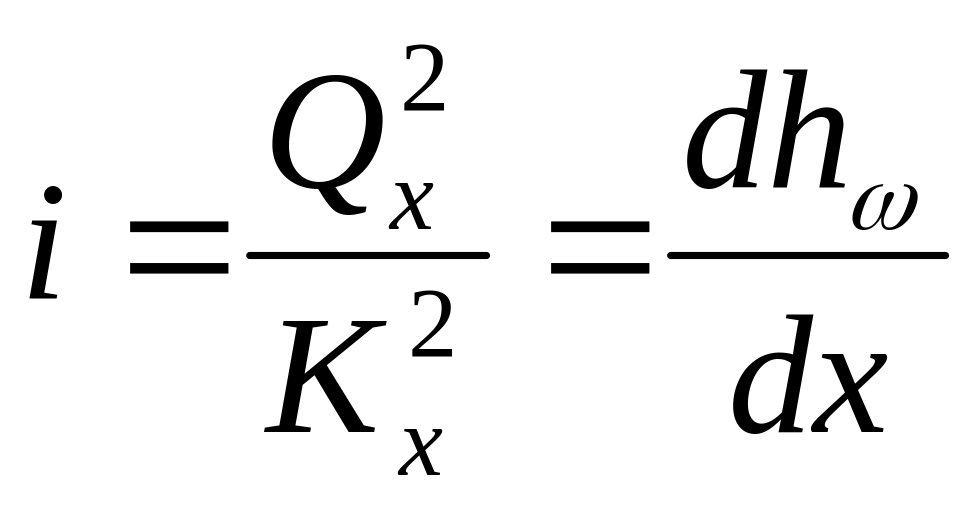или

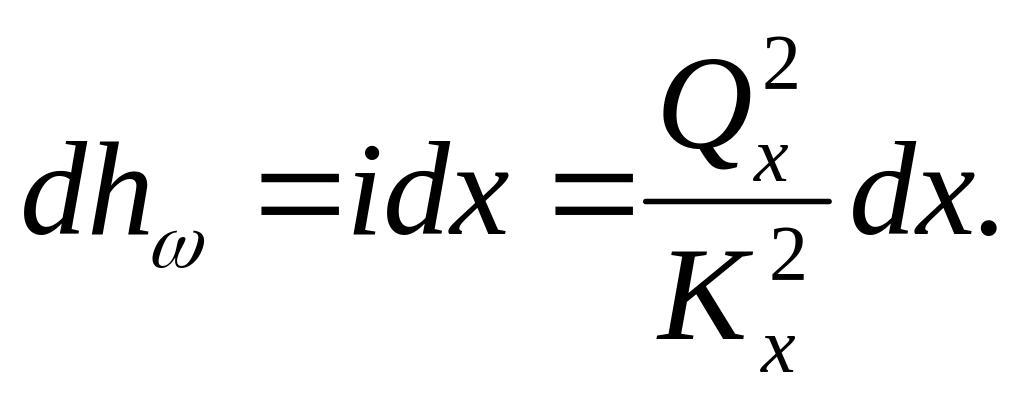
Здесь –потери напора на участке . К –расходная характеристика трубы.

Тогда

.

Но .

Следовательно,

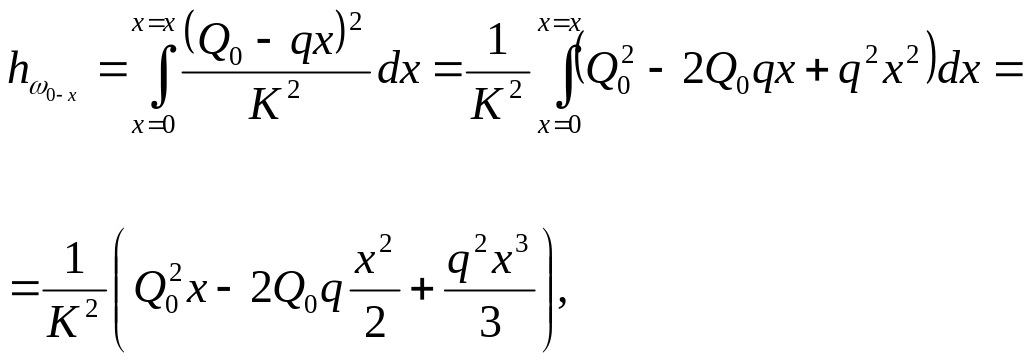
или

.

Для построения пьезометрической линии найдем уравнение пьезометрической линии. Очевидно, что в сечении n-n гидростатический напор , следовательно, уравнение пьезометрической линии можно записать в виде

.

Потеря напора на участке длиной

.

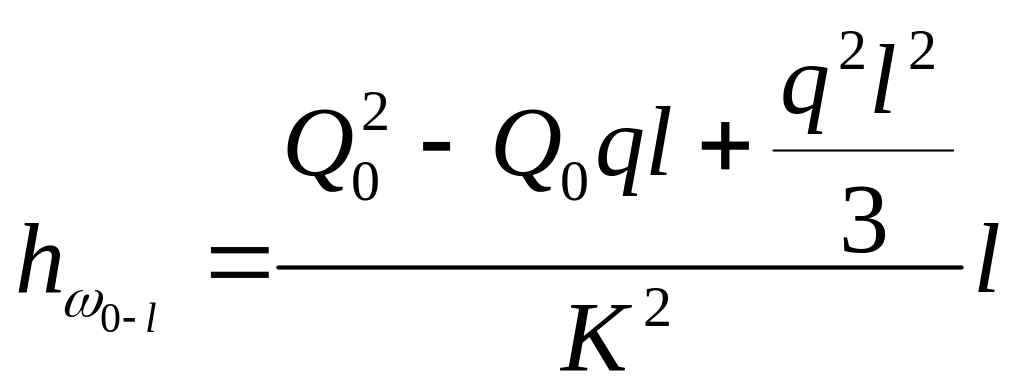Так как , где –расход, уходящий из трубы через щель на пути , то для всего участка

.

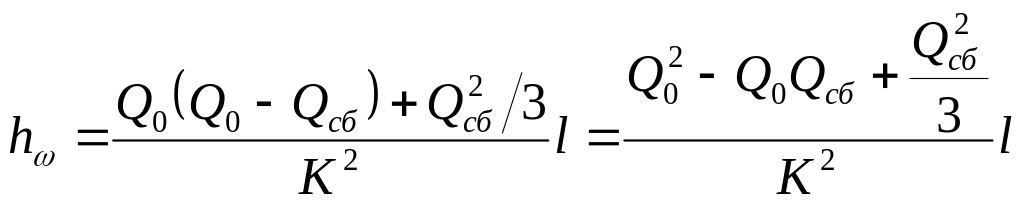Если транзитный расход равен нулю, то и мы получим

Из последнего выражения видно, что при непрерывной раздаче расхода на участке потери напора на трение в три раза меньше по сравнению с потерями напора при транспортировке всего расхода , когда непрерывная раздача отсутствует.

7.9. Расчет распределительной

тупиковой водопроводной сети

При расчете могут встретиться два случая:

1) расчет новой сети, когда отсутствует заранее заданный напор в начальном пункте ( отметка уровня воды в водонапорной башне);

2) расчет распределительной сети с заданным напором в голове системы, что имеет место при подключении сети к уже имеющемуся водонапорному баку или существующему трубопроводу.

Рассмотрим случай, когда отметка горизонта воды в водонапорной башне неизвестна (рис.11).

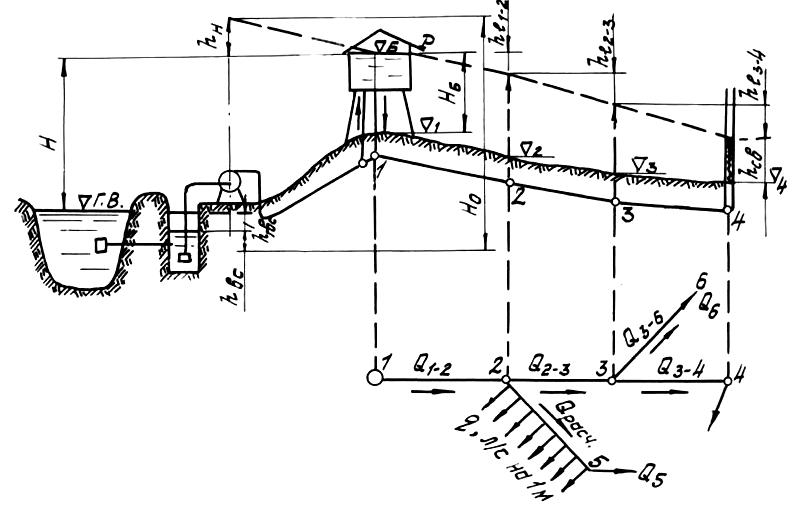Рис.11

Исходные данные:

а) длины участков сети, их расположение в плане, отметки земли по трассе трубопровода;

б) узловые расходы, т.е. расходы, отбираемые в отдельных точках сети ( );

в) расходы q, отбираемые с 1 м длины того или иного участка сети (в данном случае участка 2-5);

г) свободные напоры в отдельных точках (узлах) сети, т.е. отсчитываемые от поверхности земли, последние заданы, например, , , , .

Задача гидравлического расчета в данном случае:

а) определить диаметры d труб на отдельных участках сети;

б) определить отметку горизонта в водонапорной башне, обеспечивающую подачу требуемых расходов в заданные точки сети.

Порядок расчета

1. Устанавливаем расчетные расходы для отдельных участков сети. Расчетный расход какого-либо участка сети должен равняться сумме расходов, забираемых на сети ниже по течению этого участка. Например, 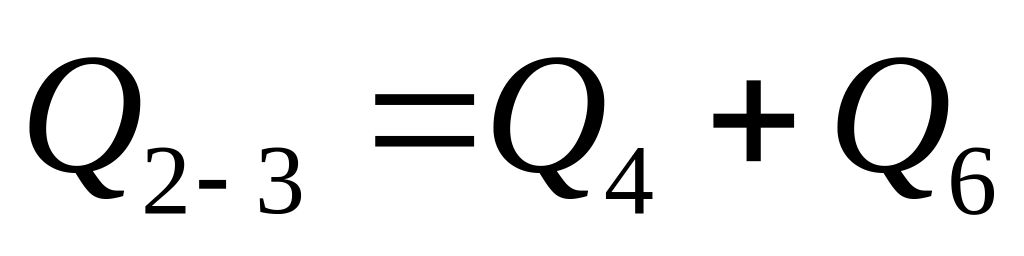. Расчетный расход для участка 2–5 составляет

.

2. Намечаем в сети линию, которую принимаем за магистральную. Такой линией должна быть линия, по которой пропускается наибольший расход, имеющая наибольшую длину и проходящая по наиболее высоким отметкам поверхности земли. В данном случае это линия 1–2–3–4.

Если в качестве магистральной будет выбрана линия, не отвечающая перечисленным требованиям, то в отдельные конечные точки ответвления не будут поступать требуемые расходы. На это будет указывать то, что в этих конечных пунктах отметки пьезометрической линии будут выше, чем в узлах, расположенных выше (по течению).

3. Рассчитываем магистральную линию, для чего:

а) задаемся для каждого участка магистрали так называемой экономической скоростью . Величина этой скорости зависит от диаметра труб (чем больше диаметр, тем больше ). Численные значения экономических скоростей для различных диаметров приводятся в справочной литературе, например в таблицах Ф.А. Шевелева или в таблице УП приложения в задачнике по гидравлике А.В. Андреевской, Н.Н. Кременецкого и М.В. Пановой;

б) задавшись скоростями для каждого участка магистрали определяем диаметры труб из соотношения

,

где

,

откуда

.

Найденные значения диаметров округляем до ближайшего (большего или меньшего) стандартного (сортаментного) значения;

в) для полученных значений диаметра, пользуясь таблицей [5], определяем соответствующие значения расходной характеристики К;

г) вычисляем для каждого участка магистрали потери напора по длине по формуле

;

д) зная потери напора для каждого участка магистрали, строим пьезометрическую линию Р–Р, начиная с конца магистрали, поскольку отметка нам задана.

4. Определяем отметку горизонта воды в баке водонапорной башни по формуле

,

где –суммарные потери напора по длине всей магистрали.

Отметка обусловливает высоту водонапорной башни.

5. Рассчитываем ответвления. Целью этого расчета является подбор диаметра труб для каждого ответвления, обеспечивающего в конечном пункте свободный напор не меньше требуемого.

Поскольку мы уже построили пьезометрическую линию для магистрали, тем самым мы установили отметки этой линии, т.е. напоры, в начале каждого ответвления, а напоры в концах ответвлений нам заданы.

Порядок расчета ответвлений:

а) вычисляем потери напора по длине для каждого ответвления по формуле , где –отметки пьезометрической линии соответственно в начале и конце ответвления;

б) из формулы для потери напора по длине определяем значения расходной характеристики для каждого ответвления

;

в) по таблице для полученных значений находим соответствующие значения диаметра, причем последние округляются до ближайшего большего стандартного значения;

г) по найденным округленным значениям диаметра определяем значения расходной характеристики и вычисляем действительные потери напора по длине , после чего уточняем свободные напоры в концах ответвления.