7.4 Гидравлический расчет простого короткого трубопровода

Исходными уравнениями для гидравлического расчета являются уравнение Бернулли и уравнение неразрывности. Рассмотрим истечение жидкости из простого короткого трубопровода в атмосферу. Напишем уравнение Бернулли для сечения 1–1 и 2–2 относительно плоскости отсчета 0–0 (рис.7):

.

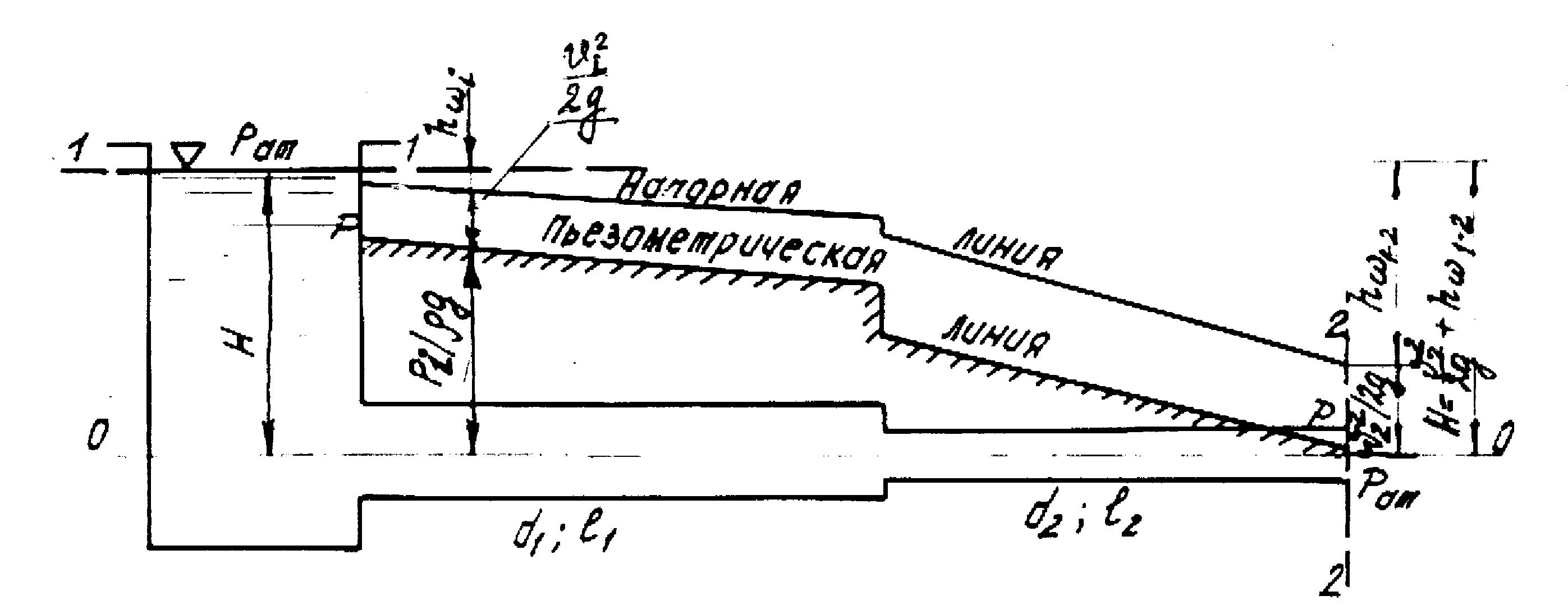
Рис.7

Обозначая и учитывая, что , ; , получим:

, (7.20)

где

.

Таким образом, при истечении жидкости в атмосферу часть действующего напора Н преобразуется в скоростной напор, а часть затрачивается на преодоление гидравлических сопротивлений на участке между рассматриваемыми сечениями 1–1 и 2–2.

Выражая потери по длине и в местных сопротивлениях общими формулами

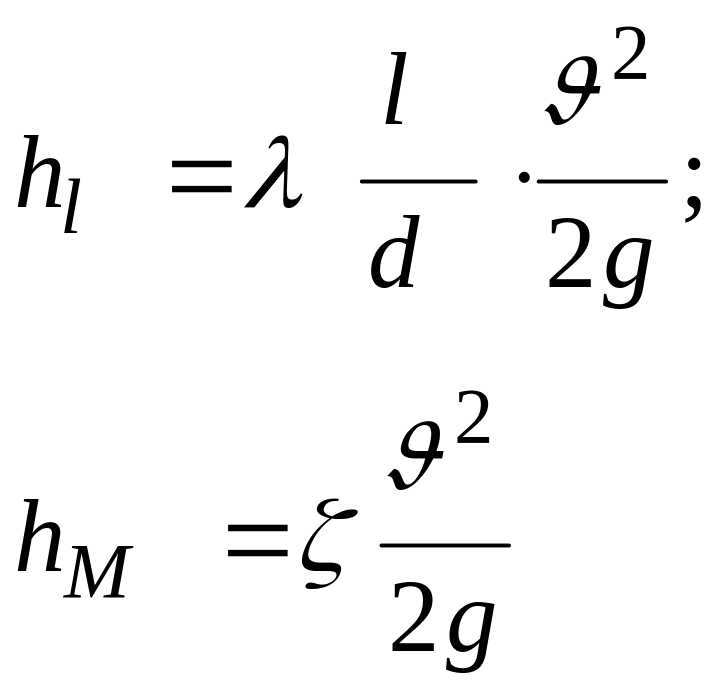
и выражая все потери через скорость , получим

.

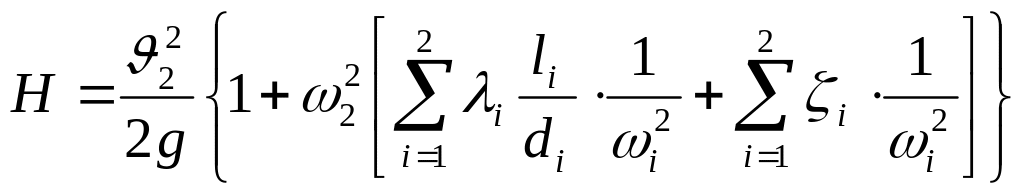Решая это уравнение относительно скорости , получим:

,

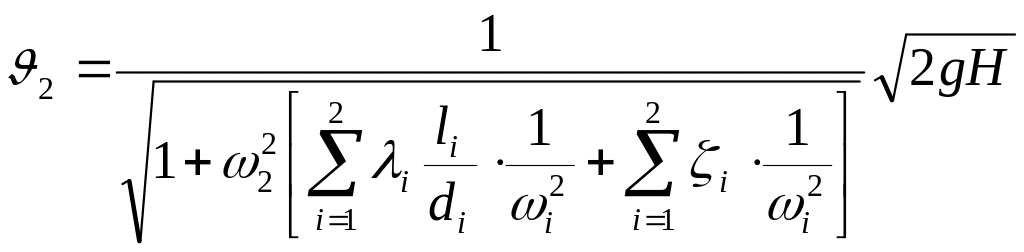а для расхода

,

где

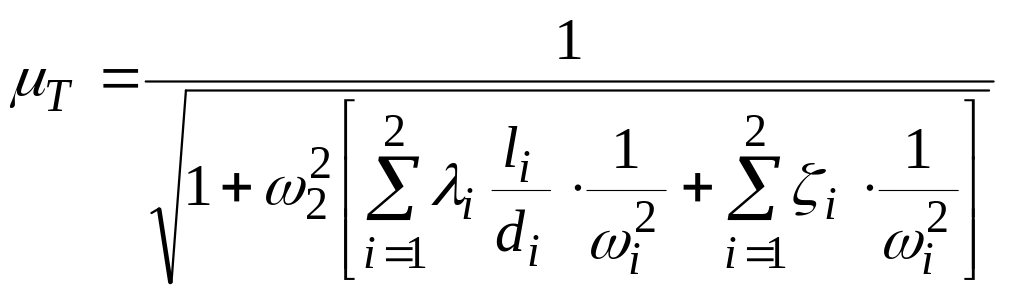
может быть назван коэффициентом расхода трубопровода.

Если участки трубопровода имеют большую длину, то местными потерями или пренебрегают, или учитывают способом эквивалентной длины трубы. Согласно этому способу местные сопротивления с потерей напора заменяют в расчете участком трубы длиной , выбираемой так, чтобы потеря по длине на ней равнялась бы . Тогда из условия

находят эквивалентную длину

7.5. Основные задачи по расчету простых

длинных трубопроводов в квадратичной области сопротивления

1. Определение расхода воды Q при заданных: диаметре d, длине l и потере напора .

2. Определение потери напора при заданных данных: диаметре трубопровода d, длине l и расходе воды Q.

3. Определение необходимого диаметра трубопровода d при заданных: расходе воды Q, длине трубопровода l и потере напора .

Общий порядок решения задач

1. По заданному d из таблиц находим К, тогда

.

2. Для заданного диаметра d находим из таблиц соответствующее значение расходной характеристики К и тогда вычисляем

.

3. Вычисляем величину требуемого модуля расхода.

.

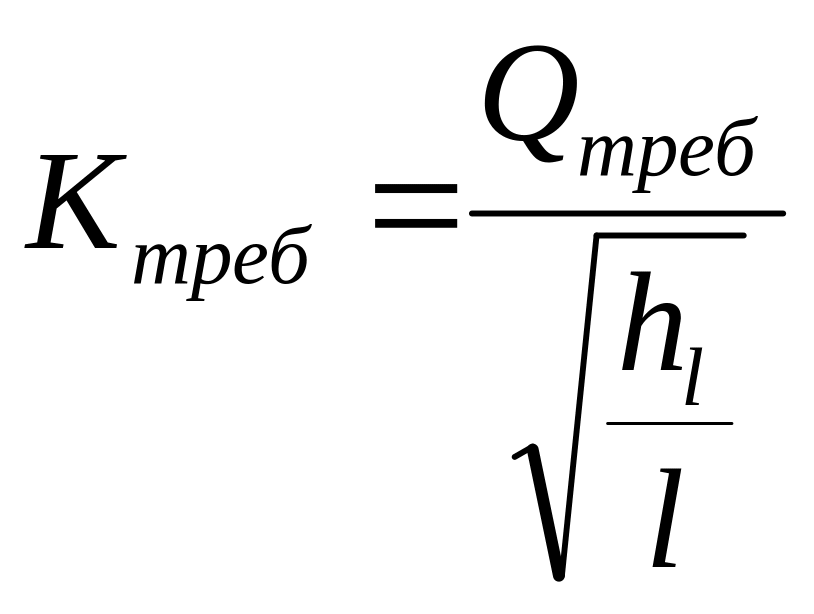Далее, в таблице, где приведены значения К, находим величину, равную . Если такой величины в таблице нет, то берем ближайшее большее значение и отвечающее ему значение диаметра, которое и будет искомым.

7.6. Гидравлический расчет простого

длинного трубопровода с последовательным соединением труб

Пусть дан трубопровод, состоящий из n последовательно соединенных участков с различными диаметрами.

Очевидно, что для трубопровода (рис.8) общая потеря напора по всей его длине определяется как сумма потерь напора на отдельных участках, т.е.:

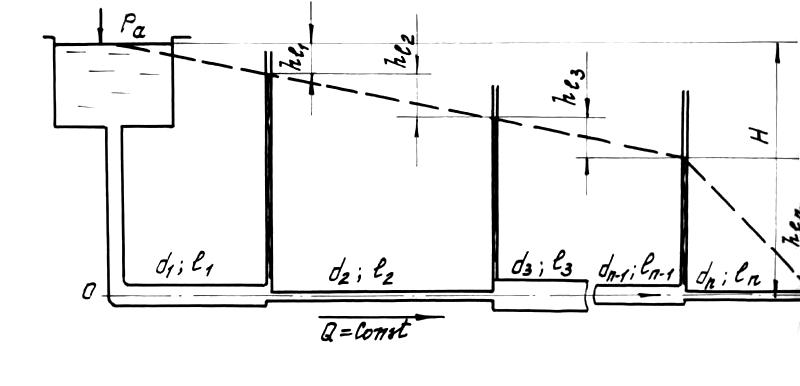
Рис.8

Для определения потерь напора по длине на каждом участке воспользуемся формулой . Таким образом,

; ;… .

При этом считаем, что

.

Следовательно, общая потеря напора по длине трубопровода будет равна

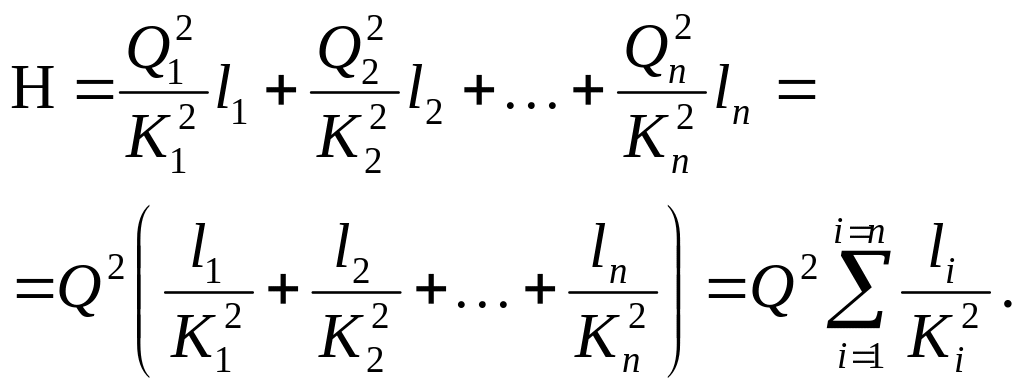
Общий ход решения трех основных задач в этом случае тот же, что и при гидравлическом расчете длинного простого трубопровода постоянного сечения.

В ряде случаев для облегчения гидравлического расчета последовательно соединенных труб с переменным сечением его удобно заменять эквивалентным трубопроводом. Эквивалентным трубопроводом называется трубопровод постоянного сечения (d=const), в котором суммарная величина потерь напора при постоянном расходе будет такой же, как и в трубопроводе, составленном из участков труб различного диаметра.

Согласно определению, можно написать, что

Здесь общая длина трубопровода

При заданных диаметрах и длинах участков, пользуясь таблицей, нетрудно вычислить

и определить величину расходной характеристики эквивалентного трубопровода:

.

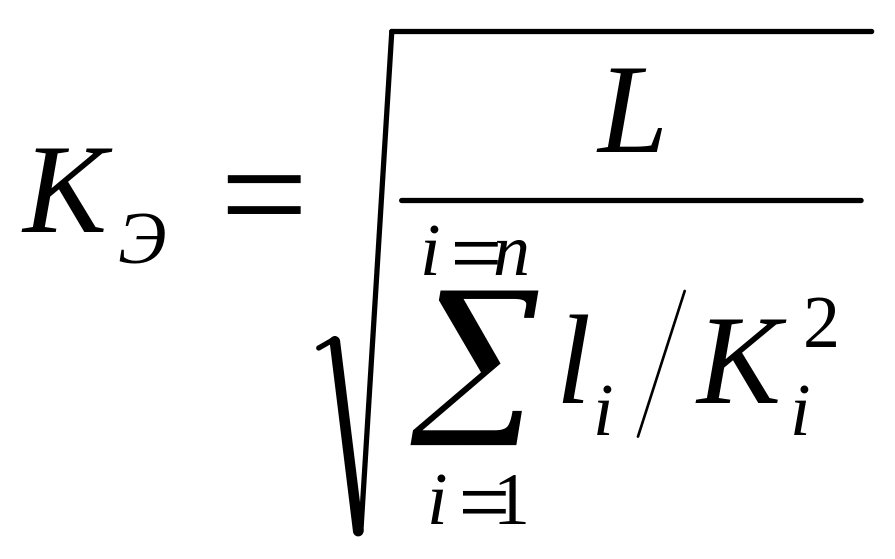Зная расходную характеристику , можно по таблицам подобрать и диаметр эквивалентного трубопровода .