2.2. Дифференциальные уравнения равновесия
идеальной жидкости (уравнения Л. Эйлера)
Выделим в покоящейся жидкости элементарный прямоугольный параллелепипед (рис.2), т.е. длины его ребер dx, dy, dz считаем бесконечно малыми величинами. Оси прямоугольных координат направим параллельно ребрам параллелепипеда. В центре тяжести каждой грани параллелепипеда приложим силу гидростатического давления, замещающую действие на нее окружающей массы жидкости. Эти силы согласно первому свойству гидростатического давления будут направлены по нормали внутрь параллелепипеда. Каждая из рассматриваемых сил равна произведению гидростатического давления в центре тяжести данной грани параллелепипеда на ее площадь.
Обозначим гидростатическое давление в центре тяжести параллелепипеда (точка А) через р. Учитывая непрерывность изменения давления в жидкости, т.е. функциональную зависимость (2.2), найдем, что гидростатические давления в центрах тяжести граней параллелепипеда отличаются от давления в точке А соответственно на
;
и
.
В связи с изложенным силы гидростатического давления будут равны:
(2.3)
Кроме сил гидростатического давления (поверхностных сил) на рассматриваемый параллелепипед действуют массовые силы, непрерывно распределенные по его объему (в данном случае силы тяжести). Равнодействующую массовых сил dG можно представить как произведение ускорения g массовой силы на массу жидкости в объеме параллелепипеда:
dG=g· ·dx·dy·dz, (2.4)
где –плотность жидкости.
Полагаем, что плотность жидкости постоянна, т.е. =const. Следовательно, жидкость рассматривается как несжимаемая.
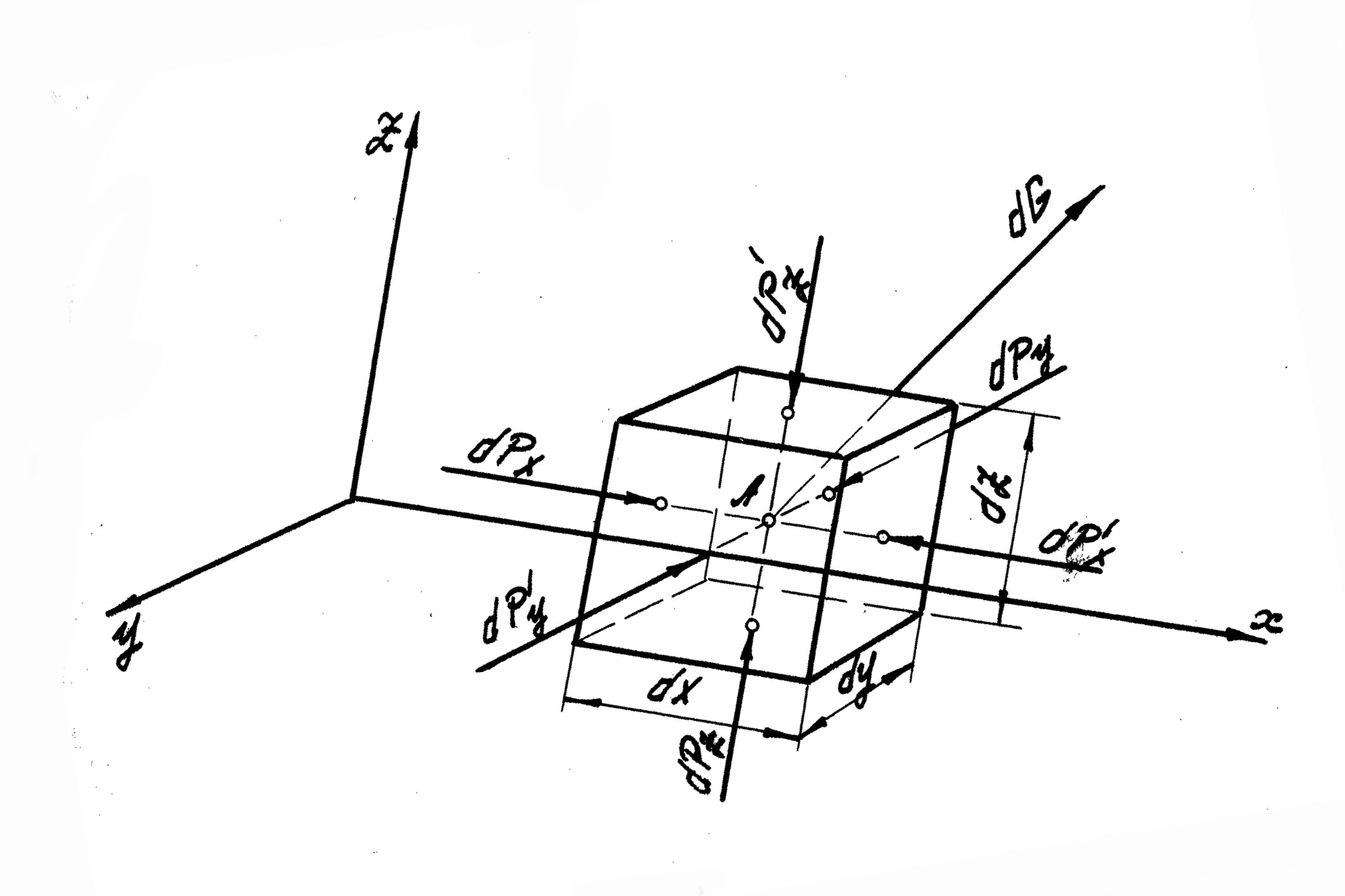
Рис.2
Обозначив проекцию ускорения g на оси ОX, OY, ОZ соответственно через X, Y, Z, получим выражения для проекции силы dG на эти оси:
(2.5)
Параллелепипед находится в равновесии, поэтому суммы проекции сил на каждую координатную ось должны быть равны нулю. Запишем выражения сумм для каждой оси (ОX, OY, ОZ соответственно):
(2.6)
Раскрыв скобки и разделив каждое из уравнений на массу параллелепипеда dxdydz, т.е. приведя каждый член уравнения к единице массы рассматриваемого объема жидкости, получим систему дифференциальных уравнений равновесия идеальной жидкости:
(2.7)
Эти уравнения впервые были выведены в 1755 году Л. Эйлером, поэтому их часто называют уравнениями Эйлера.
2.3. Интегрирование дифференциальных уравнений равновесия
идеальной жидкости
Умножая уравнения (2.7) соответственно на dx, dy и dz и складывая их, получим
.
(2.8)
Поскольку р = f(x,y,z), выражение в скобках в правой части уравнения (2.8) есть полный дифференциал гидростатического давления, следовательно,
(Xdx
+ Ydy + Zdz)=dp.
(2.9)
Уравнение (2.9) есть основное уравнение гидростатики в дифференциальной форме.
Проинтегрируем уравнение (2.9) для случая, когда жидкость заключена в вертикальном цилиндрическом сосуде и находится в покое под действием силы тяжести и внешнего давления на ее свободной поверхности (рис. 3).
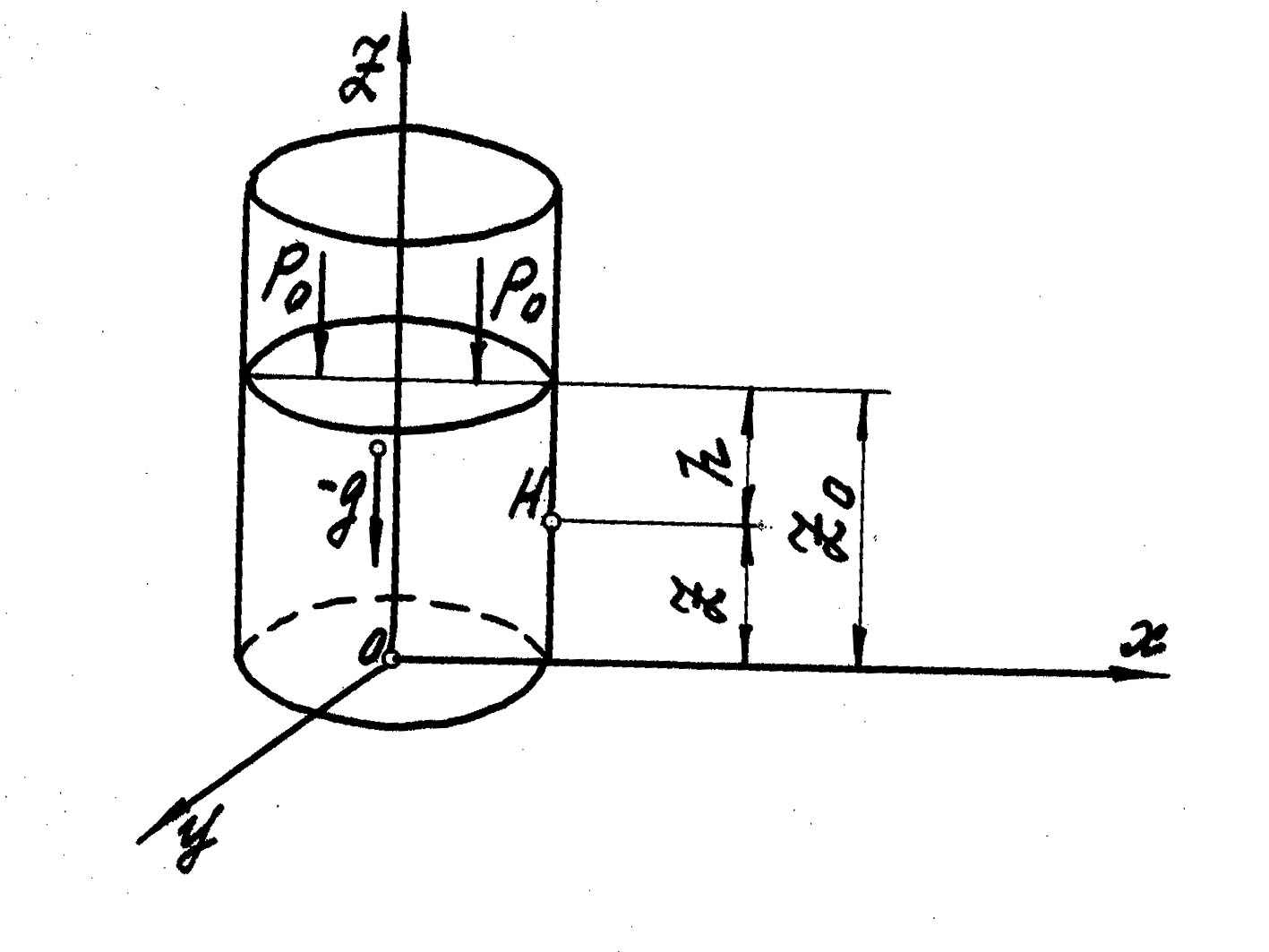
Рис.3
Горизонтальная плоскость XOY называется плоскостью сравнения.
Для рассматриваемого случая, составляющие единичной силы тяжести по координатным осям будут равны:
Х= 0; Y= 0; Z= - g, и отсюда
dp= - g·dz. (2.10)
p= - g·Z+C. (2.11)
При р = р0 и Z = Z0
C = p0 + gZ0,
поэтому уравнение (2.11) примет вид
p = - g · Z + р0+ gZ0 , (2.12)
или
p = p0 + g(Z0 -Z) = p0 + gh, (2.13)
p = p0 + gh, (2.14)
,
(2.15)
.
(2.16)
Уравнения (2.14) и (2.15) – это две разновидности основного уравнения гидростатики.
Уравнение (2.14) является математическим выражением закона распределения гидростатического давления в жидкости: величина гидравлического давления в некоторой точке, погруженной на глубину h относительно свободной поверхности, равна сумме внешнего давления на свободную поверхность жидкости р0 и давления от веса столба жидкости с площадью основания, равной единице, и высотой, равной глубине погружения h рассматриваемой точки.
Помимо этого уравнение (2.14) показывает, что внешнее давление р0, которое действует на поверхность жидкости, передается всем точкам жидкости без изменения. В этом заключается суть закона Паскаля.