7.2. Гидравлические характеристики трубопроводов
При гидравлическом расчете трубопроводов используются графические методы расчета, в основе которых лежит построение так называемых гидравлических характеристик трубопровода.
Функциональная зависимость потерь напора от расхода h=f(Q) может быть изображена графически (рис.1). Для этого достаточно, задаваясь различными значениями расхода Q, вычислить соответствующие этим значениям потери и напора h по одной из расчетных формул простого трубопровода.
Кривая на рис.1, графически отображающая изменение потерь напора в данном трубопроводе от величины пропускаемого им расхода, называется характеристической кривой, или гидравлической характеристикой трубопровода.
Рассмотрим построение суммарных гидравлических характеристик: а)для простого трубопровода, составленного из труб разного диаметра; б)сложного трубопровода, состоящего из нескольких трубопроводов, соединенных параллельно.
В случае последовательного соединения трубопроводов (см.рис.4) на одном графике строят характеристики отдельных последовательно включенных участков трубопровода.
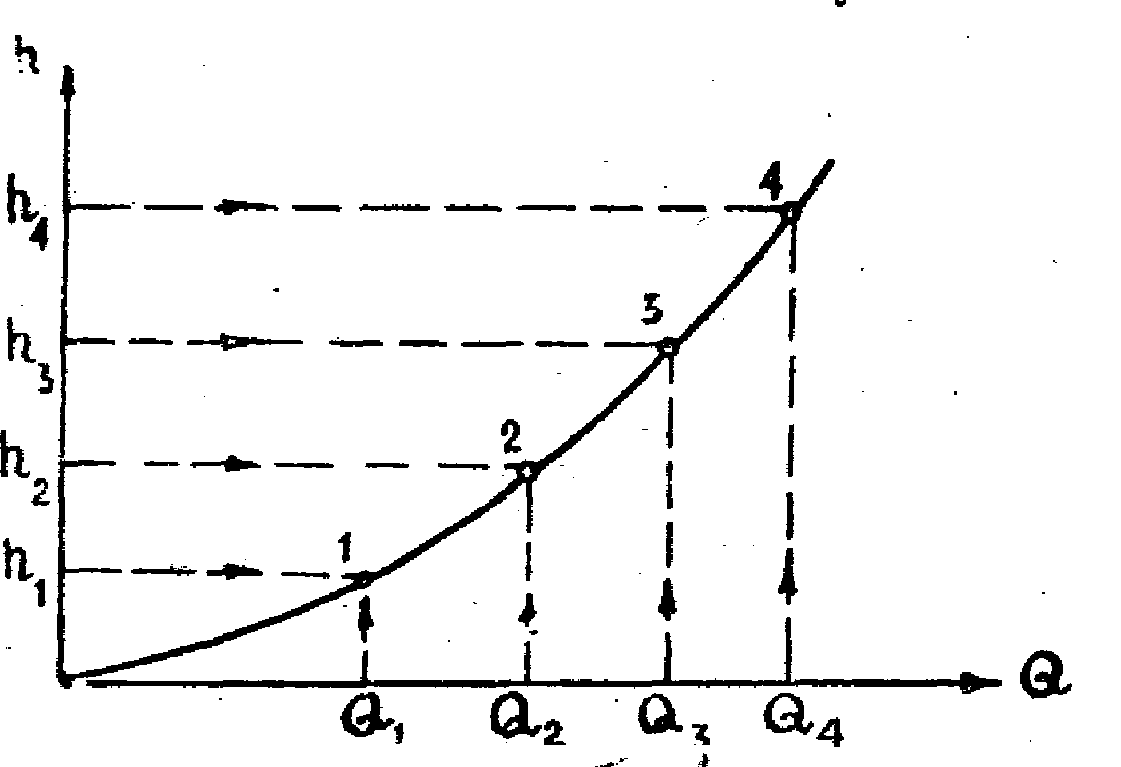
Рис.1
Эти кривые приведены на рис.2, где кривая I –гидравлическая характеристика первого участка с диаметром d1, кривая II –характеристика второго участка с диаметром d2, кривая III –характеристика третьего участка с диаметром d3.
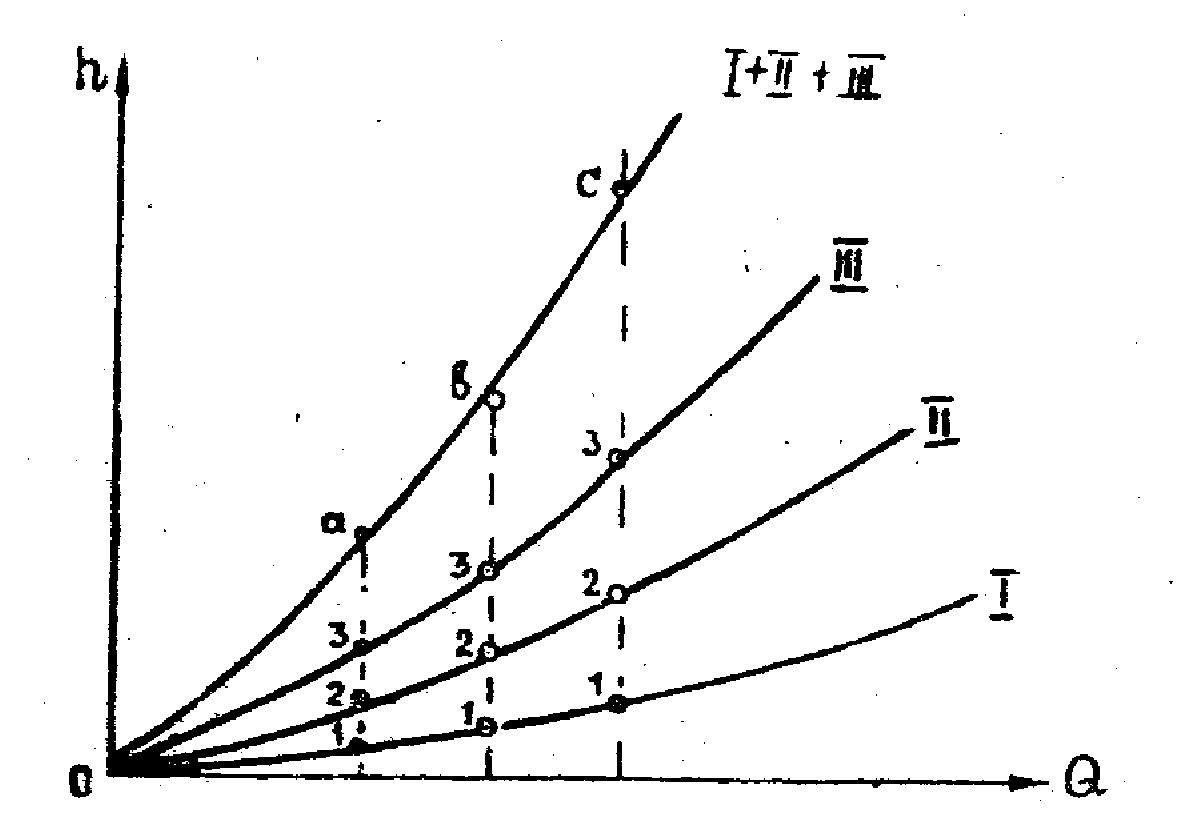
Рис.2
Из ранееизложенного известно, что при последовательном соединении суммируются потери напора. Для построения суммарной гидравлической характеристики всего трубопровода необходимо сложить характеристики отдельных участков по вертикали. Для этого проведем ряд вертикальных прямых, параллельных оси ординат, каждая из которых пересечет все три кривые в точках 1, 2, 3, и сложим при постоянных абсциссах ординаты точек пересечения этих прямых с кривыми.
В результате мы получим ряд точек: а, b, с,..., принадлежащих новой кривой I+II+III, которая и представляет собой искомую суммарную характеристику всего трубопровода.
При параллельном соединении также надо прежде всего построить гидравлические характеристики отдельных параллельно включенных участков (кривые I, II, III на рис.4).
При параллельном соединении общий расход определяется как сумма расходов в отдельных параллельных участках; потери напора в этих участках одинаковы по величине и полная потеря напора определяется как потеря в одном из них.
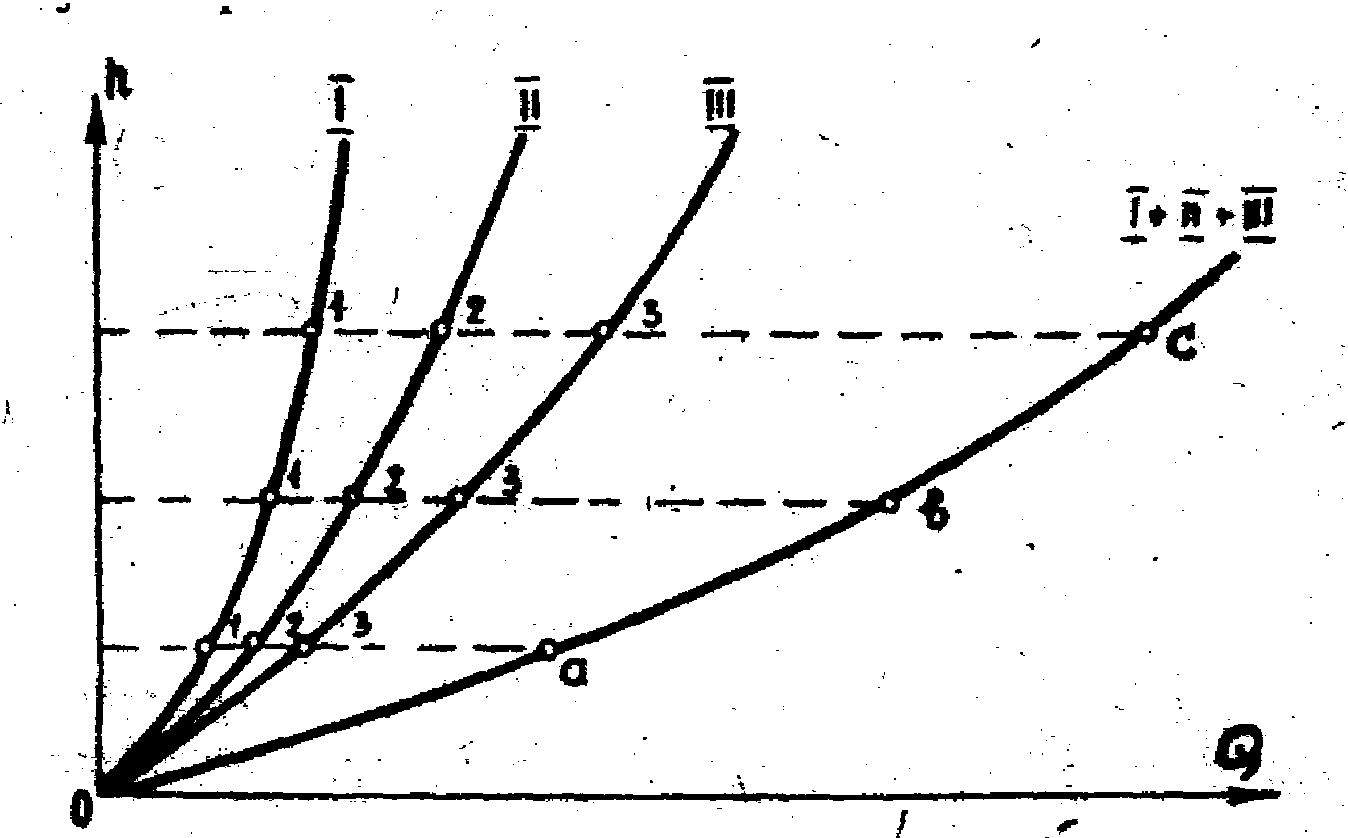
Рис.4
Исходя из этого проводим ряд горизонтальных прямых параллельно оси абсцисс и складываем при постоянных ординатах абсциссы точек их пересечения с характеристиками отдельных участков. В результате сложения получим ряд точек а, в, с..., определяющих суммарную характеристику I+II+III трубопровода три параллельном соединении.
Изложенный метод построения гидравлических характеристик трубопроводов справедлив также и для ламинарного режима, при котором потеря напора графически будет изображаться гидравлическими характеристиками в виде прямых линий с уравнением h=S'Q.
7.3. Понятие о длинных и коротких трубопроводах
При гидравлическом расчете напорные трубопроводы разделяются на длинные и короткие.
К длинным трубопроводам относятся трубопроводы, в которых местные потери напора пренебрежимо малы по сравнению с потерями напора по длине.
При гидравлическом
расчете таких трубопроводов местными
потерями напора или пренебрегают вовсе,
считая, что
,
или принимают их ориентировочно в
размере 5-10% от потерь напора по длине,
то есть
К коротким трубопроводам относятся трубопроводы небольшой длины, например всасывающие трубы насосных станций и сифоны. В этих трубопроводах местные потери напора являются величинами одного порядка с потерями напора по длине. Поэтому при гидравлическом расчете коротких трубопроводов вычисляются потери отдельно для каждого местного сопротивления.
Длинные напорные трубопроводы подразделяются на простые и сложные. Простым считается трубопровод постоянного или переменного диаметра без ответвлений (рис.5а,б). Сложным является трубопровод постоянного или переменного диаметра, имеющий одно или несколько ответвлений. Сложные трубопроводы, в свою очередь, подразделяются на незамкнутые (тупиковые), рис.6а и на замкнутые (кольцевые), рис.6 б,в.
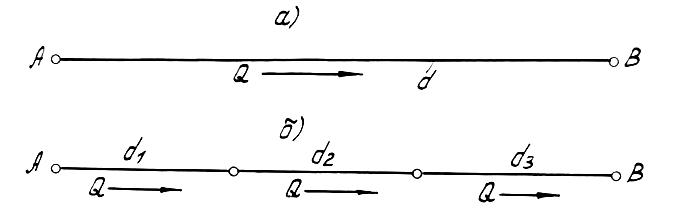
Рис.5
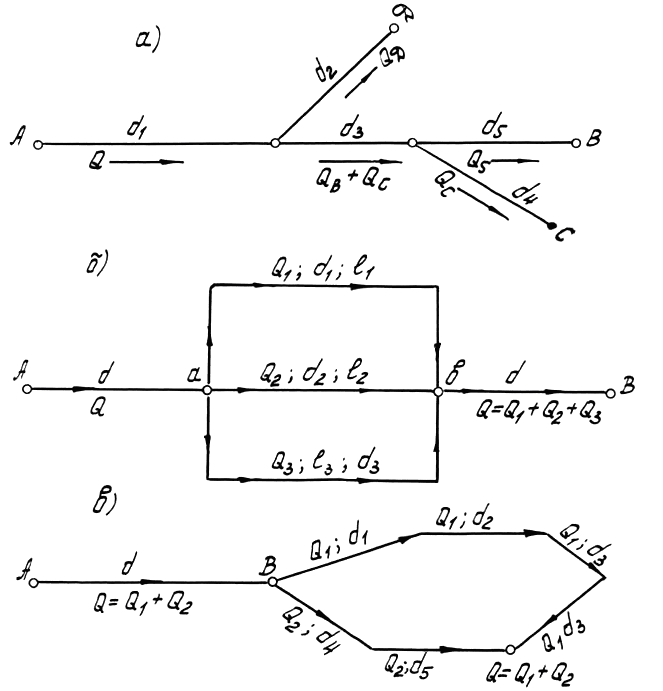
Рис.6