6.5. Незатопленная турбулентная струя

В этой струе можно выделить три характерные части: компактную, раздробленную и распыленную (рис.7).

В пределах компактной части струя сохраняет цилиндрическую форму, а сплошность потока еще не нарушается. В пределах раздробленной части сплошность струи нарушается, причем наблюдается ее постепенное расширение. Наконец, в пределах распыленной части струи происходит распад потока на отдельные капли. Разрушение струи, т.е. ее раздробление, а затем и распыление, объясняется аэрацией струи. Аэрация же, в свою очередь, обусловливается действием сил собственного веса жидкости и сил сопротивления воздуха, вызывающих турбулентный обмен частиц через границу между воздушной и водяной средами.

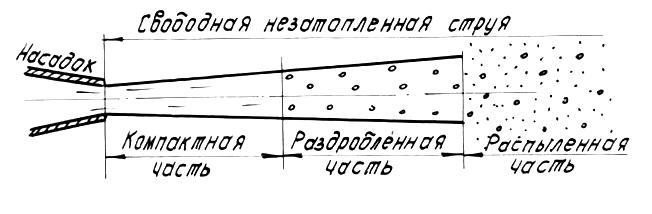
Рис.7

Уравнение теоретической траектории свободной струи выводится из предположения, что все частицы движутся совершенно одинаково, причем каждая, как свободная материальная точка в пустоте. В этом случае уравнение траектории (рис.8) в параметрической форме может быть представлено в виде:

(6.24)

(6.25)

где –начальная скорость; –угол наклона вектора начальной скорости к горизонту; –время.

Исключая время, получим

(6.26)

Полагая в последней формуле y=0, определим –теоретическую дальность полета струи (дальность боя), откуда следует, что теоретическая максимальная дальность боя будет при

, (6.27)

. (6.28)

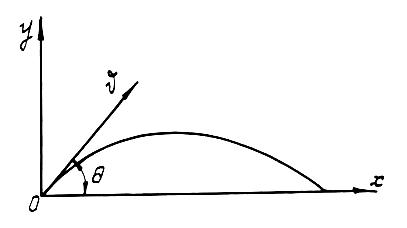
Рис.8

Формула (6.28) дает хорошее совпадение с опытом лишь при напорах истечения

На дальность боя и высоту подъема струи оказывают влияние сопротивление воздуха и ветер. При этом на дальность боя ветер влияет больше, чем на высоту подъема.

Свободная незатопленная вертикальная струя, покидающая насадок со скоростью , направленной вертикально вверх, теоретически поднимается, как это следует из формулы (6.25), на высоту :

Глава седьмая

НАПОРНОЕ УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ

В ЦИЛИНДРИЧЕСКИХ ТРУБОПРОВОДАХ

7.1. Основные зависимости для гидравлического расчета

трубопроводов при равномерном напорном движении жидкости

Из формулы потерь напора по длине при турбулентном режиме движения жидкости можно получить выражение для средней скорости при напорном равномерном движении жидкости.

Преобразуем эту формулу, учитывая, что d=4R:

откуда

.

Обозначим

. (7.1)

Тогда

, (7.2)

или

. (7.3)

Формула (7.2) так же, как и (7.3), называется формулой Шези.

Эта формула широко применяется в гидротехнической практике для расчета средней скорости потока в каналах, лотках, реках и безнапорных трубах.

Коэффициент с в формуле Шези имеет размерность корня квадратного из ускорения, что непосредственно следует из уравнения (7.1).

В практике расчетов величину с при квадратичной области сопротивления принято определять по эмпирическим и полуэмпирическим формулам. Среди эмпирических формул наибольшее распространение получила формула Н.Н Павловского

, (7.4)

где –коэффициент шероховатости русла, зависящий от материала стенок и их состояния; –гидравлический радиус, м. –показатель степени, зависящий от и .

Н.Н. Павловский считает возможным применять формулу (7.4) при и

Из формулы Шези можно получить ряд зависимостей, которые широко применяются при гидравлических расчетах как напорных, так и безнапорных трубопроводов и открытых русл.

Разделив формулы (7.2) и (7.3) на , получим соответственно

(7.5)

(7.6)

откуда следует

(7.7)

(7.8)

Здесь –модуль скорости (расходная характеристика); – модуль расхода (расходная характеристика).

Решив формулы (7.2) и (7.3) относительно уклона I, получим

; (7.9)

. (7.10)

Умножив выражения (7.6) и (7.7) на , найдем

; (7.11)

. (7.12)

Обозначив получим

, (7.13)

или

,

где величина , равная потере напора на единицу длины трубопровода, при расходе, равном единице, носит название удельного сопротивления трубопровода.

Формулу (7.13) можно записать в виде

, (7.14)

где S –сопротивление трубопровода.

Величины К, А, и S представляют собой обобщенные гидравлические параметры трубопровода, использование которых значительно ускоряет гидравлический расчет.

Зависимости (7.8), (7.12), (7.13) и (7.14) являются основными расчетными формулами простого трубопровода при равномерном движении жидкости.

Если область сопротивления будет отличаться от квадратичной, фактическое значение расходной характеристики К определяется по следующему выражению:

, (7.15)

где

. (7.16)

Значения коэффициента , полученные Ф. А. Шевелевым для основных видов водопроводных труб, приводятся в справочной литературе.

С учетом (7.15) расчетные зависимости (7.8) и (7.12) примут вид

(7.17)

и

. (7.18)

Формулу (7.18) можно также представить в виде

, (7.19)

где –длина трубопровода, км, а значение приводится также в справочной литературе.