6.2. Истечение жидкости из насадков при постоянном напоре

Рассмотрим истечение жидкости в атмосферу через внешний круглоцилиндрический насадок (насадок Вентури) – рис.3:

–длина насадка;

–площадь поперечного сечения насадка на выходе;

–площадь отверстия, к которому присоединен насадок.

Как видим, при выходе в среду атмосферного давления сжатие струи отсутствует.

Водоворотная область так же, как и транзитная струя в пределах этой области, характеризуется наличием вакуума. Причем максимальный вакуум наблюдается в сечении С–С, где струя имеет наибольшее сжатие и где скорости в транзитной струе, а также кинетическая энергия жидкости оказываются наибольшими.

Известно, что с возрастанием кинетической энергии потока в рассматриваемом сечении потенциальная энергия должна уменьшаться.

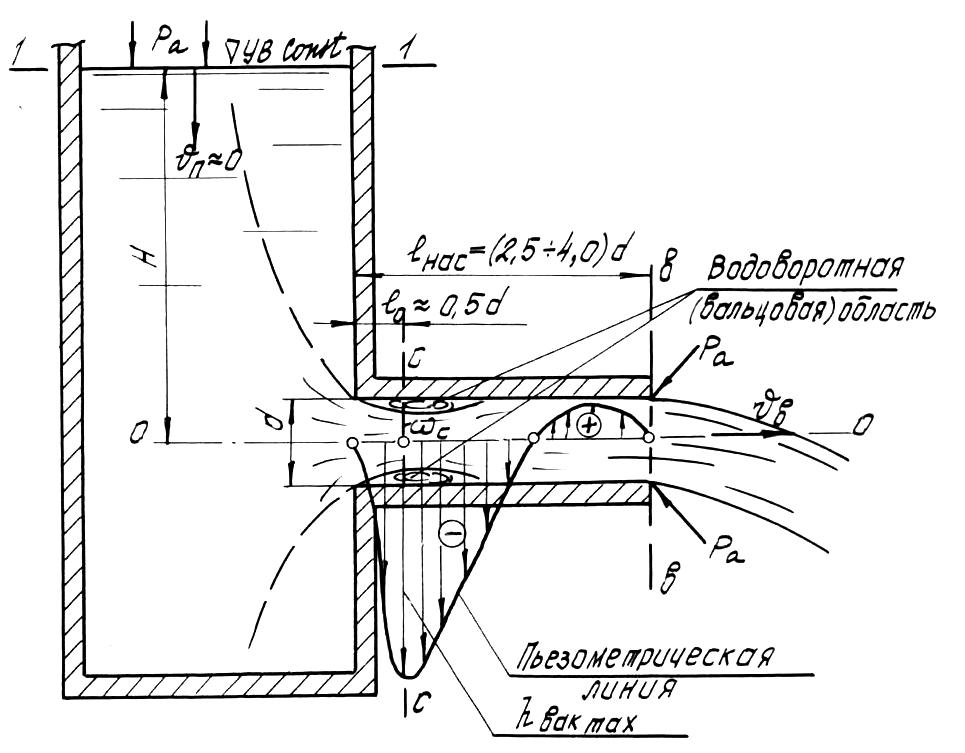
Рис.3

Если в сечении имеем атмосферное давление, то, двигаясь от этого сечения против течения и попадая в область, где скорости благодаря сжатию струи оказываются большими, чем в сечении , мы получим давление в этой области меньше, чем в сечении , т.е. меньше атмосферного давления.

Пьезометрическая линия для насадка в соответствии со сказанным получает вид, показанный на рис.2.

Найдем расчетные зависимости для и Q. Для этой цели соединим уравнения Бернулли сечения 1–1 и (см.рис.3) и , рассуждая точно так же, как и в случае истечения жидкости через отверстия, получаем следующие расчетные формулы:

, (6.10)

. (6.11)

Расход Q при истечении из насадка

,

где –коэффициент расхода насадка,

,

так как для насадка коэффициент сжатия, отнесенный к сечению , где давление атмосферное, равен единице, то есть =1,0.

Численные значения коэффициентов

Коэффициент для сечения С–С равняется коэффициенту сжатия при истечении от отверстия в тонкой стенки, т.е.

.

Коэффициент сопротивления , при истечении из насадка в атмосферу, равен коэффициенту сопротивления на вход в трубу, т.е.

.

При истечении под уровень

.

Коэффициенты скорости и расхода насадка как в случае истечения в атмосферу, так и в случае истечения под уровень, равны, т.е.

,

или

.

Сопоставим расходы и скорости при истечении жидкости через круглое отверстие в тонкой стенке и через насадок Вентури, приставленный к этому отверстию:

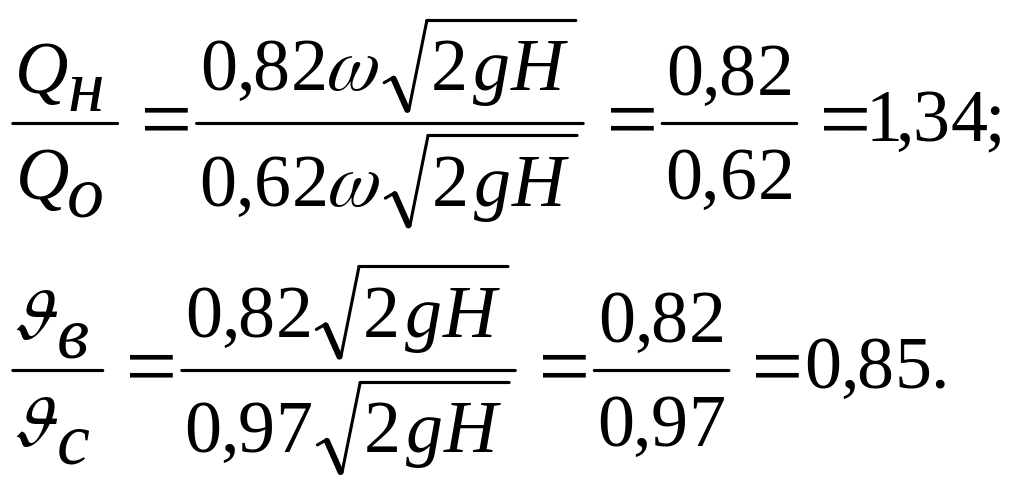
Как видно, внешний цилиндрический насадок, присоединенный к отверстию, дает следующий эффект:

а) расход жидкости, вытекающей из сосуда, увеличивается на 34%;

б) скорость истечения жидкости уменьшается на 15%.

Увеличение расхода обусловлено наличием вакуума в насадке. Благодаря вакууму напор истечения вырастает, становясь равным . Уменьшение же скорости обусловлено увеличением потерь напора в связи с расширением струи в насадке (между сечениями С–С и ).

Величину вакуума в сечении С–С можно найти, если соединить уравнение Бернулли сечения С–С и .

(6.12)

где

; (6.13)

. (6.14)

Подставив (6.13) и (6.14) в (6.12), получаем

(6.15)

или

(6.16)

Подставив в (16) вместо его значение из формулы (10), будем иметь

(6.17)

Если в (6.17) подставить численные значения коэффициентов и , получим

или

(6.18)