5.12. Местные гидравлические сопротивления

При течении вязкой жидкости через места резкого изменения формы пограничных поверхностей труб и каналов, как, например, расширения, сужения, повороты и т.п., изменяется поле скоростей и образуются области, заполненные крупными и мелкими вихрями. Кинематическая структура течения с образованием отрывов потока от стенок и вихревых зон показана на рис.10 а, б и 11 а, б. Крупные вихри интенсифицируют процесс диссипации (рассеивания) энергий , благодаря чему потери в местных сопротивлениях могут намного превосходить потери по длине участка той же протяженности, что и местное сопротивление.

Структура потока, размеры и интенсивность вихрей существенно зависят от режима течения, т.е. от числа Рейнольдса.

Основные виды местных потерь напора можно условно разделить на следующие группы:

а) потери, связанные с изменением живого сечении потока (т.е. его средней скорости), наблюдающиеся в случае резкого и плавного расширения в трубопроводах;

б) потери, вызванные изменением направления потока, что встречается в различного рода коленах, угольниках, и отводах, используемых в трубопроводах;

в) потери, связанные с протеканием жидкости через различного типа арматуру (вентили, краны, обратные клапаны, сетки и т.д.);

г) потери, связанные с отделением одной части потока от другой, или слиянием двух потоков в один общий, что наблюдается в тройниках, крестовинах и отверстиях в боковых стенках трубопровода при наличии транзитного расхода.

Потери напора в местных сопротивлениях определяются формулой Вейсбаха (5.17).

Коэффициент , входящий в формулу, определяется экспериментально для каждого местного сопротивления.

Исключение составляют некоторые частные случаи при квадратичной области сопротивления, для которых при определенных допущениях удается найти теоретическую зависимость .

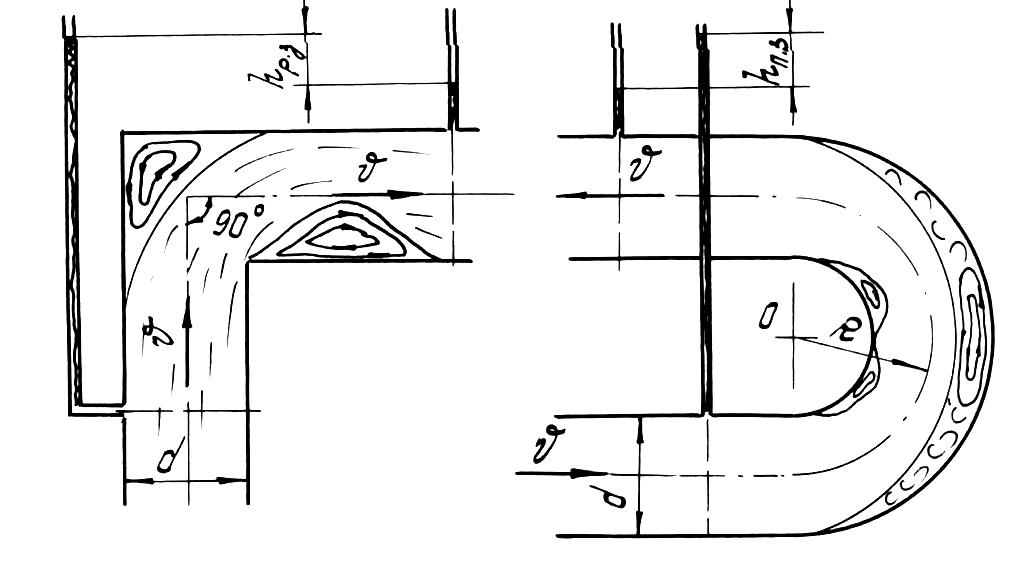
а) б)

Рис.10

На рис. 10 представлена схема движения потока жидкости на повороте: а) при резком (без закругления) повороте; б) при плавном повороте.

а)

б)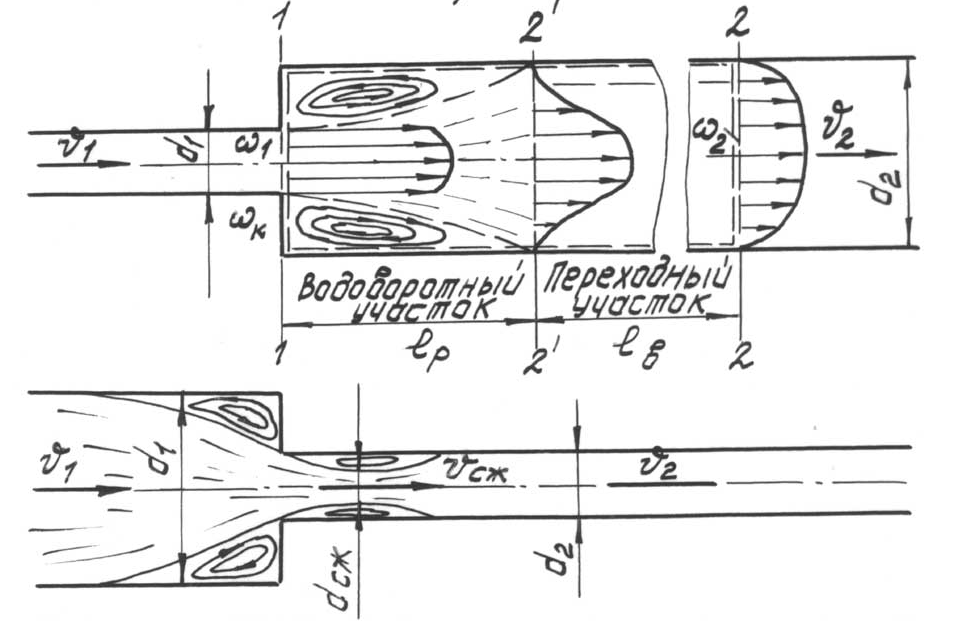

Рис.11

На рис. 10 представлена схема движения потока жидкости при резком изменении поперечного сечения трубопровода: а)резком расширении потока; б)сужении потока.

Результаты экспериментальных исследований разных авторов показывают, что при больших числах Re имеет место область квадратичного сопротивления, где значение коэффициента зависит только от конфигурации граничных поверхностей и не зависит от рода жидкости и скорости течения.

При малых же числах Re значение коэффициента зависит не только от Re, но и от размеров потока и геометрических форм, граничных поверхностей.

Численные значения коэффициентов для различных местных сопротивлений, наиболее часто встречающихся в инженерной практике, приводятся в гидравлических справочниках.

Рассмотрим подробнее местное сопротивление в виде внезапного расширения трубы (см. рис. 11). Наблюдения показывают, что при выходе струи из узкой части трубы образуется отрыв потока от стенок и пространство между струей и стенками заполняется вихрями. На некотором расстоянии струя полностью расширяется, но может иметь в сечении резко неравномерную эпюру скоростей, что обусловлено нарушением оссемметричности (искривлением) потока на участке . Выравнивание эпюры скоростей происходит на участке , в конце которого (сечение 2–2) устанавливается распределение скоростей, характерное для стабилизированного турбулентного потока. Поскольку перестройка эпюры скоростей сопровождается дополнительными потерями (помимо потерь на трение), то в расчетный участок местного сопротивления включает , полагая = + . Выбрав расчетные сечения 1–1 и 2–2, как показано на рис.11а, выразим потери на внезапное расширение по уравнению Бернулли

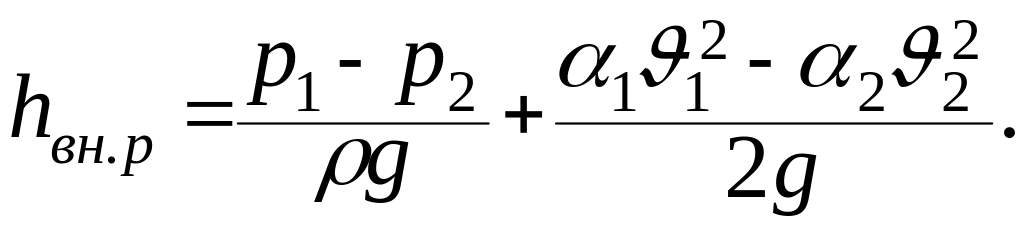(5.63)

В дальнейшем (для простоты) будем полагать, что = =1.

Чтобы исключить разность давлений, применим к отсеку жидкости, ограниченному сечениями 1–1 и 2–2 и боковой поверхностью трубы (контрольная поверхность на рис.2 показана штриховой линией), уравнение количества движения

(5.64)

где –корректив количества движения, который для сечений 1–1 и 2–2 можно принять равным единице; –проекция на направление движения внешней силы трения , действующей со стороны стенок трубы на рассматриваемый отсек жидкости. Так как длина участка потока между сечениями 1–1 и 2–2 невелика, то силой пренебрегаем и считаем =0 (1-е допущение). –проекция собственного веса отсека на направление движения, =0; –сумма проекций на ось S сил гидродинамического давления и , действующих соответственно на торцевые сечения 1–1 и 2–2 выделенного отсека транзитной струи; R – проекция реакции стенок; величина , где R –давление вертикальной стенки, имеющей кольцевую форму.

Величину можно представить в виде

(5.65)

Измерения показывают, что в сечении 2–2 давление распределяется по гидростатическому закону, а в пределах кольцевой площади мало отличается от давления . При этом можем написать:

;

.

Упростив уравнение (5.65) и учтя уравнение неразрывности , находим

Следовательно,

.

Теперь уравнение Бернулли (5.63) можно записать в виде

или, после упрощений

.

Эта формула, называемая формулой Борда, показывает, что потеря напора при внезапном расширении потока равна скоростному напору, вычисленному по потерянной скорости ( ). Учитывая уравнение неразрывности, формулу Борда нетрудно привести к виду, аналогичному формуле Вейсбаха (5.17), и получить теоретическое выражение для коэффициента сопротивления .

Действительно, поскольку , то

,

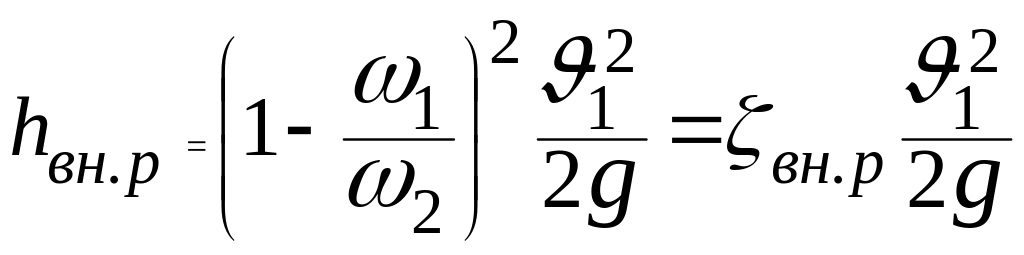и, следовательно,

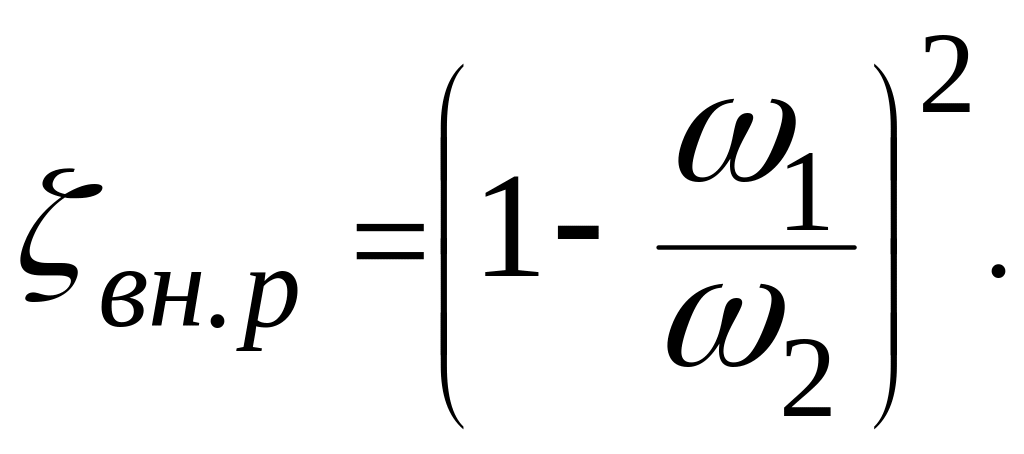(5.66)

В частном случае, когда , т.е. имеет место сопряжение трубы с большим резервуаром, будет или .При пользовании формулой (5.66) необходимо иметь в виду допущения, исходя из которых она выведена. Одним из них является предположение о близости к единице коэффициентов и . Поэтому при значительной неравномерности распределения скоростей перед расширением (когда эти коэффициенты существенно отличны от единицы) формула (5.66) требует уточнения. Такое уточнение можно получить, если при выходе не делать допущения о том, что . Другое ограничение формулы Борда связано с влиянием на числа Рейнольдса. Оно проявляется при , а при малых числах Re становится преобладающим, поэтому формула (5.66) может давать удовлетворительные результаты лишь при квадратичной области сопротивления.

Заметим, наконец, что согласно выводу формулой Борда учитываются только потери на расширение, т.е. то превышение местных потерь над потерями по длине на участке, равном расчетному участку , которое вызвано увеличением диссипации энергии в местном сопротивлении. Если расчетный участок = + велик, то потери на трение здесь могут быть сопоставимы с потерями на расширение, и пренебрегать ими нельзя. Поэтому при постановке опыта для определения потерь на расширение следует из потерь, измеренных в опыте, вычесть потери по длине на участке эквивалентной длины.

Это замечание относится и к другим видам местных сопротивлений.