
- •1.1. Системы измерения физических величин,
- •1.2. Основные физические свойства жидкостей
- •2.1. Силы, действующие в жидкости.
- •2.2. Дифференциальные уравнения равновесия
- •2.3. Интегрирование дифференциальных уравнений равновесия
- •2.4. Полное (абсолютное) и манометрическое давление.
- •2.5. Давление жидкости на плоские поверхности.
- •2.6. Положение центра избыточного давления
- •2.7. Эпюры гидростатического давления
- •2.8. Давление жидкости на криволинейные (цилиндрические) (цилиндрические) поверхности
- •2.9. Плавание тел
- •Метацентрический радиус определяется по формуле
- •3.1. Два метода изучения движения жидкости
- •3.2. Линии тока, трубка тока, траектории и струйка
- •3.3. Уравнение линии тока
- •3.4. Понятия расхода, средней скорости, живого сечения,
- •3.5. Уравнение неразрывности
- •3.6. Вихревые и безвихревые движения
- •3.7 Уравнение компонентов вихря
- •Глава четвертая основные уравнения гидродинамики
- •4.1. Основные дифференциальные уравнения движения
- •4.2. Дифференциальные уравнения движения
- •4.3. Критерии подобий и моделирование
- •4.4. Интегралы уравнения движения жидкости
- •4.5. Интеграл Лагранжа-Коши
- •4.6. Интеграл л. Эйлера
- •4.7. Интеграл д. Бернулли
- •4.8. Геометрическое и энергетическое истолкование
- •4.9. Уравнение д. Бернулли
- •4.10. Уравнение д. Бернулли
- •4.11. Гидравлический и пьезометрический уклоны
- •Гидравлические сопротивления
- •5.1. Понятие о гидравлических сопротивлениях
- •5.2. Режимы движения жидкости. Число Рейнольдса
- •5.3. Характер зависимости потерь напора
- •Для турбулентного движения
- •5.4. Основное уравнение равномерного движения
- •5.5. Общее выражение потерь напора на трение
- •5.6. Равномерное ламинарное движение жидкости
- •Распределение скоростей по сечению круглой трубы
- •Расход и средняя скорость течения
- •Потери напора на трение в круглой трубе
- •5.7. Структура турбулентного потока
- •5.8. Уравнение Рейнольдса
- •5.9. Гипотезы Буссинеска и Прандтля
- •5.10. Турбулентное движение жидкости
- •5.11. Влияние шероховатости стенки трубы
- •5.12. Местные гидравлические сопротивления
- •5.13. Определение длины влияния местных сопротивлений
- •6.1. Истечение жидкости через малые отверстия
- •6.2. Истечение жидкости из насадков при постоянном напоре
- •6.3. Свободные струи. Общие сведения
- •6.4. Затопленная турбулентная струя
- •6.5. Незатопленная турбулентная струя
- •7.1. Основные зависимости для гидравлического расчета
- •7.2. Гидравлические характеристики трубопроводов
- •7.3. Понятие о длинных и коротких трубопроводах
- •7.4 Гидравлический расчет простого короткого трубопровода
- •7.5. Основные задачи по расчету простых
- •7.6. Гидравлический расчет простого
- •7.7. Гидравлический расчет сложных трубопроводов
- •Параллельно разветвленный трубопровод
- •7.8. Гидравлический расчет простого длинного трубопровода
- •7.9. Расчет распределительной
- •7.10. Основы технико-экономического расчета трубопроводов
- •8.2. Гидравлические расчеты открытых каналов
- •8.3. Допустимые скорости
- •8.4. Движение жидкости в самотечных трубопроводах
- •Движение жидкости в пористой среде
- •9.1 Основные понятия и определения
- •9.2. Основные законы фильтрации
- •9.3. Определение коэффициента фильтрации
- •9.4. Безнапорное движение грунтовых вод
- •Разделив переменные
- •9.5. Напорное движение грунтовых вод
5.11. Влияние шероховатости стенки трубы
на коэффициент гидравлического трения
Все формулы (5.55) – (5.60) относятся к трубам с гладкой поверхностью. В действительности же поверхность трубы всегда имеет некоторую шероховатость. По форме неровностей, образующихся на поверхности, различают шероховатости зубчатую и волнистую.
Однако в качестве объекта экспериментального исследования обычно прибегают к трубам с искусственной или так называемой зернистой шероховатостью, которая создается путем приклеивания к стенке трубы сплошного и равномерного слоя песка с определенной средней величиной зерна.
В качестве обобщенной
характеристики шероховатости трубы
служит отношение её абсолютной
шероховатости, под которой понимается
средняя высота бугорков шероховатости
![]() ,
к диаметру трубы d.
Величину
,
к диаметру трубы d.
Величину
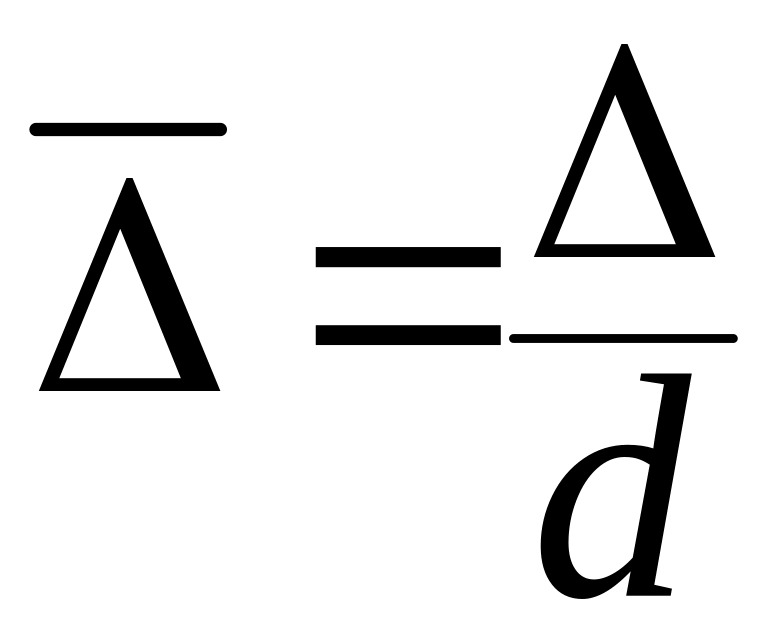 называют относительной шероховатостью
трубы. Величину
называют относительной шероховатостью
трубы. Величину
![]() для труб, выпускаемых промышленностью,
получить путем непосредственного
измерения высоты выступов шероховатости
практически невозможно. Поэтому
определяют на основе гидравлических
экспериментов при квадратической
области сопротивления. При этом находят
для рассматриваемой трубы величину
коэффициента гидравлического трения,
пользуясь формулой Дарси-Вейсбаха, а
затем из формулы Л. Прандтля
для труб, выпускаемых промышленностью,
получить путем непосредственного
измерения высоты выступов шероховатости
практически невозможно. Поэтому
определяют на основе гидравлических
экспериментов при квадратической
области сопротивления. При этом находят
для рассматриваемой трубы величину
коэффициента гидравлического трения,
пользуясь формулой Дарси-Вейсбаха, а
затем из формулы Л. Прандтля
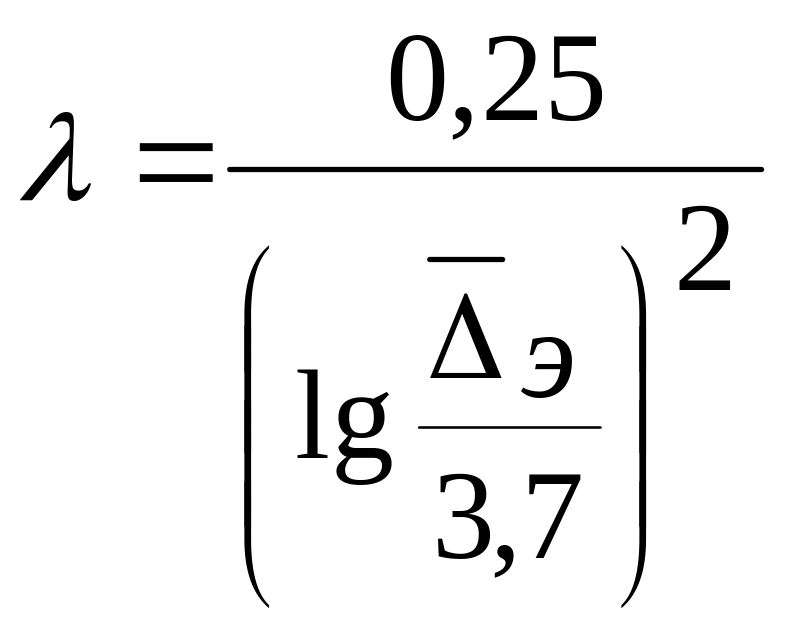 (5.62)
(5.62)
вычисляют значение
![]() а по нему –искомое значение абсолютной
эквивалентной шероховатости
а по нему –искомое значение абсолютной
эквивалентной шероховатости
![]() .
.
Величины абсолютной эквивалентной шероховатости для труб, изготовленных из различных материалов, даны в таблице.
Трубы |
Величина
|
Стеклянные Новые тянутые из латуни, свинца, меди Железные новые Чугунные новые |
0,2 – 0,8 0,1 – 1,0
20 – 50 100 – 200 |
Обширное исследование
влияния шероховатости зернистого типа
на коэффициент сопротивления круглых
труб было выполнено Никурадзе. Результаты
его опытов представлены в виде кривых
зависимости коэффициента гидравлического
трения от числа
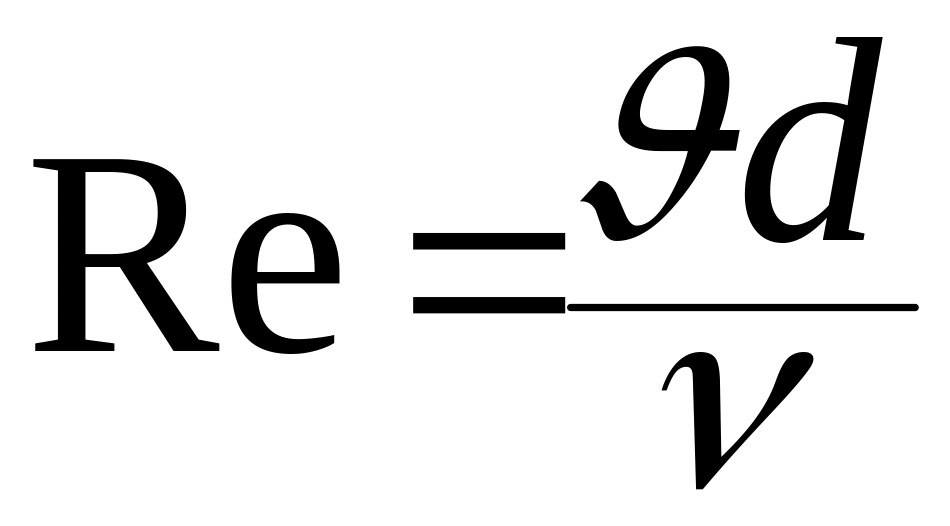 при различных
при различных
![]() .
.
Схема графика Никурадзе изображена на рис. 9.
По характеру зависимости от Re график можно разбить на три зоны.
Первая зона, линия
1, отвечающая значениям
![]() ,
(
,
(![]() ),
относится к ламинарному режиму течения,
при котором коэффициент
не зависит от относительной шероховатости
трубы и определяется по формуле (5.18), а
потери напора на трение, определяемые
формулой (5.19), оказываются пропорциональными
первой степени скорости, т.е
),
относится к ламинарному режиму течения,
при котором коэффициент
не зависит от относительной шероховатости
трубы и определяется по формуле (5.18), а
потери напора на трение, определяемые
формулой (5.19), оказываются пропорциональными
первой степени скорости, т.е
![]() .
.
Вторая зона является
переходной от ламинарного режима к
турбулентному. Коэффициент
в этой зоне, как и в первой, не зависит
от шероховатостей стенок, а зависит
только от числа Рейнольдса, т.е.
![]() .
Вторая зона соответствует числам
Рейнольдса
.
Вторая зона соответствует числам
Рейнольдса
![]() .
.
Третья зона – зона турбулентного режима, относящаяся к большим числам Рейнольдса, разбивается на три области.
1–я область (линия
2) – область гидравлически гладких труб.
В пределах этой области
не зависит от относительной шероховатости,
а зависимость этой величины от числа
Re
удовлетворяет формуле Блазиуса для
гладких труб
![]() благодаря чему
она в логарифмических координатах
изображается в виде прямой. Протяженность
этой области оказывается тем большей,
чем меньше относительная шероховатость
.
благодаря чему
она в логарифмических координатах
изображается в виде прямой. Протяженность
этой области оказывается тем большей,
чем меньше относительная шероховатость
.
Как видно из приведенных формул, в этой области
![]() .
.
Ориентировочно эта область имеет место при
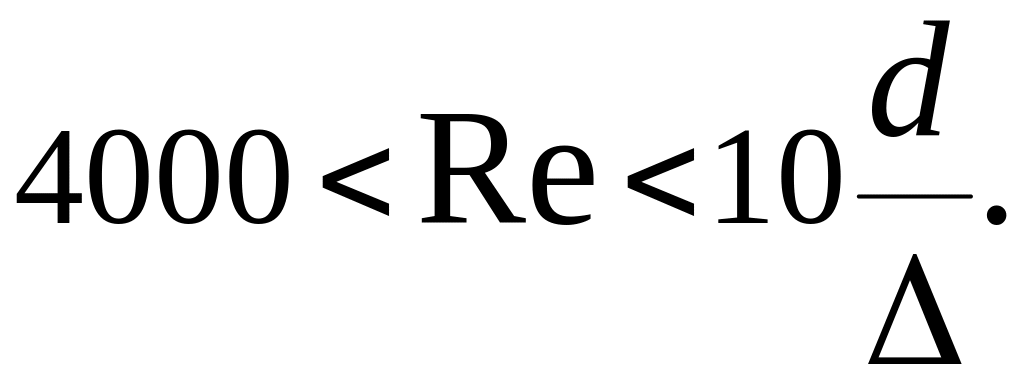
2 –я область
(заключенная между линиями 2 и АВ) –область
доквадратичного сопротивления, в которой
зависит как
от относительной шероховатости, так и
от числа Рейнольдса, а сопротивление
трубы пропорционально скорости в степени
m,
![]() ,
где m
лежит в
пределах
,
где m
лежит в
пределах
![]() .
.
Ориентировочно
эта область имеет место при
 .
Величину
в этой области сопротивления можно
определить, например, по формуле А. Д.
Альтшуля
.
Величину
в этой области сопротивления можно
определить, например, по формуле А. Д.
Альтшуля
![]() .
.
3 –я область (расположенная от линии АВ вправо) – область квадратичного сопротивления, в которой коэффициент не зависит от числа Рейнольдса, а является лишь функцией относительно шероховатости. С ростом последней увеличивается, при этом начало указанной области сдвигается в сторону меньших значений числа Рейнольдса. В этой области сопротивления величина коэффициента может быть определена, например, по формуле (5.59), а также по формуле Прандтля-Никурадзе
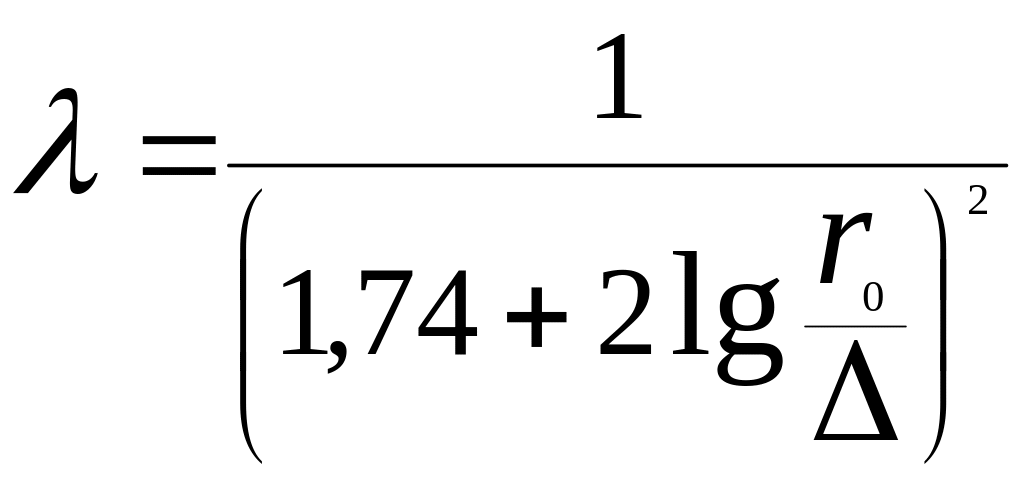 .
.
Перечисленные особенности для зависимости от числа Рейнольдса при турбулентном режиме движения жидкости можно объяснить на основе сопоставления средней высоты бугорков шероховатости с толщиной ламинарного подслоя .
При
![]() ,
что имеет место при сравнительно малых
числах Рейнольдса, бугорки шероховатости
полностью покрыты ламинарным подслоем
и их обтекание не сопровождается
вихреобразованием. Следовательно, в
этом случае шероховатость не влияет на
коэффициент гидравлического трения и
труба ведет себя в гидравлическом
отношении как гладкая, подчиняясь закону
сопротивления Блазиуса (первая область
третьей зоны на графике Никурадзе).
,
что имеет место при сравнительно малых
числах Рейнольдса, бугорки шероховатости
полностью покрыты ламинарным подслоем
и их обтекание не сопровождается
вихреобразованием. Следовательно, в
этом случае шероховатость не влияет на
коэффициент гидравлического трения и
труба ведет себя в гидравлическом
отношении как гладкая, подчиняясь закону
сопротивления Блазиуса (первая область
третьей зоны на графике Никурадзе).
Толщина ламинарного
подслоя уменьшается с увеличением числа
Рейнольдса, и при достаточно больших
значениях последнего оказывается, что
![]() .
В этом случае бугорки шероховатостей
практически целиком оказываются в
турбулентном ядре потока и их обтекание
происходит с образованием вихрей. При
таком характере обтекания силы вязкости
малы по сравнению с инерционными силами,
и коэффициент гидравлического трения
перестает зависеть от числа Рейнольдса
(область квадратичного сопротивления
отвечает случаю, когда
и
оказываются
величинами одного и того же порядка).
.
В этом случае бугорки шероховатостей
практически целиком оказываются в
турбулентном ядре потока и их обтекание
происходит с образованием вихрей. При
таком характере обтекания силы вязкости
малы по сравнению с инерционными силами,
и коэффициент гидравлического трения
перестает зависеть от числа Рейнольдса
(область квадратичного сопротивления
отвечает случаю, когда
и
оказываются
величинами одного и того же порядка).
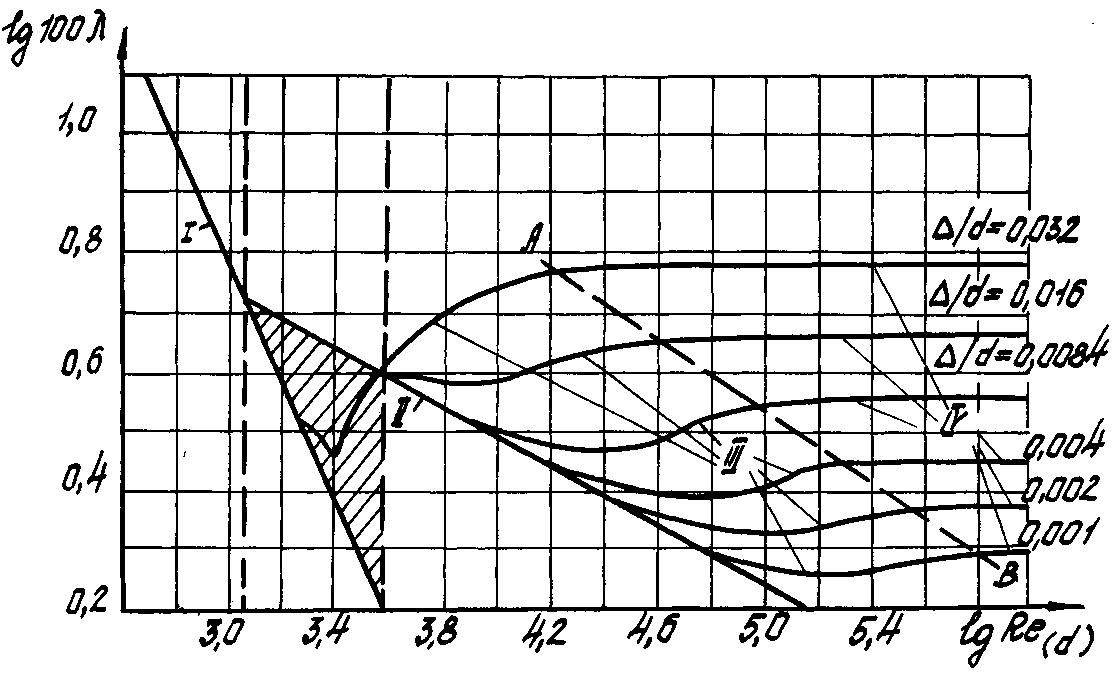
Рис.9
