Для турбулентного движения

.

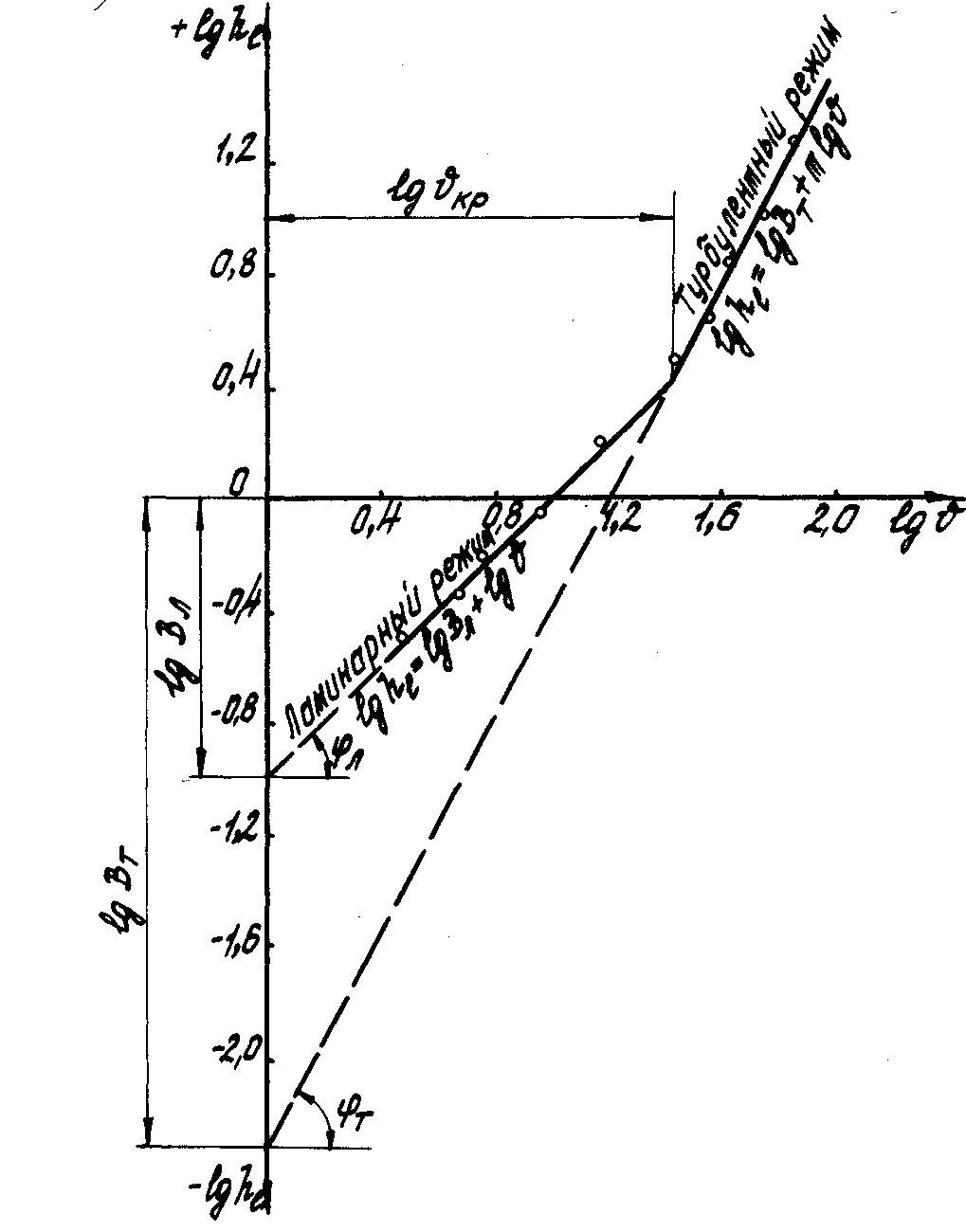
Рис.2

Здесь также получили прямую, но угловой коэффициент этой прямой другой и равен , в то время как в первом случае мы имели (см. рис. 2).

Различие кинематической структуры ламинарного и турбулентного потоков изменяет характер зависимости потери по длине от средней скорости .

Турбулентные пульсации порождают дополнительные касательные напряжения, которые обуславливают увеличение потерь энергии в турбулентных потоках, по сравнению с ламинарными, при сопоставимых условиях.

5.4. Основное уравнение равномерного движения

в цилиндрической трубе

Равномерное движение возможно лишь в трубах постоянного сечения, так как при равномерном движении величина средней скорости и распределение скоростей по сечению должны оставаться неизменными по длине трубопровода.

Найдем выражение для равномерного движения жидкости в трубах, справедливое как для ламинарного, так и турбулентного режимов.

Пусть в наклонном трубопроводе имеем равномерное движение со средней скоростью .

Сечениями 1-1 и 2-2 в трубопроводе выделим соосную цилиндрическую струйку радиусом и длиной (рис. 3).

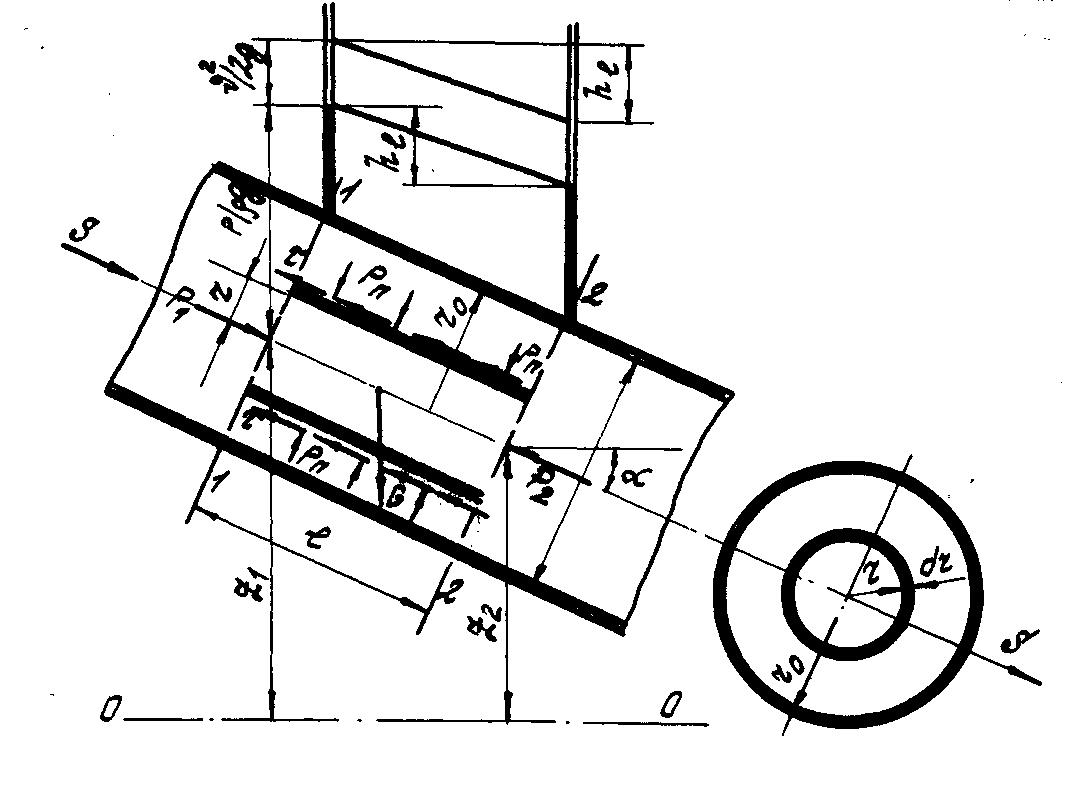
Рис.3

Для выделенного отсека уравнение динамического равновесия относительно оси движения S-S можно записать в виде

где –сумма проекций внешних сил на ось движения; –сумма проекций сил сопротивления на ось движения.

Внешние силы:

1. Сила тяжести проекция которой на ось равна:

, (5.7)

где

2. Силы давления на торцевые поверхности отсека: и .

Сумма проекций этих сил на ось S-S будет

(5.8)

3. Силы давления на боковую поверхность направлены перпендикулярно к оси движения S-S, поэтому проекции этих сил будут равны нулю.

4. Суммарная сила сопротивления (трения) спроектируется на ось движения в натуральную величину и может быть выражена зависимостью

(5.9)

где –сила сопротивления трения, приходящаяся на единицу боковой поверхности выделенного жидкого цилиндра (среднее касательное напряжение). Таким образом, с учетом выражений (5.7)–(5.9) уравнение динамического равновесия (5.6) можно представить в виде

. (5.10)

Разделив уравнение (10) на произведение , получим

. (5.11)

Поскольку левая часть уравнения (11) представляет собой в случае равномерного движения потерю напора по длине , можно это уравнение окончательно записать в виде

(5.12)

или

, (5.13)

где –гидравлический или пьезометрический уклоны, так как при равномерном движении эти уклоны равны.

Уравнение (5.13) является основным уравнением равномерного движения жидкости в цилиндрической трубе.

5.5. Общее выражение потерь напора на трение

при равномерном движении жидкости в трубах

Касательное напряжение в соответствии с формулой (4.13) распределяется по живому сечению потока по линейному закону (рис. 4).

Оно равно нулю на оси трубы (r=0) и принимает максимальное значение на ее стенке ( ), где

откуда следует, что

, (5.14)

. (5.15)

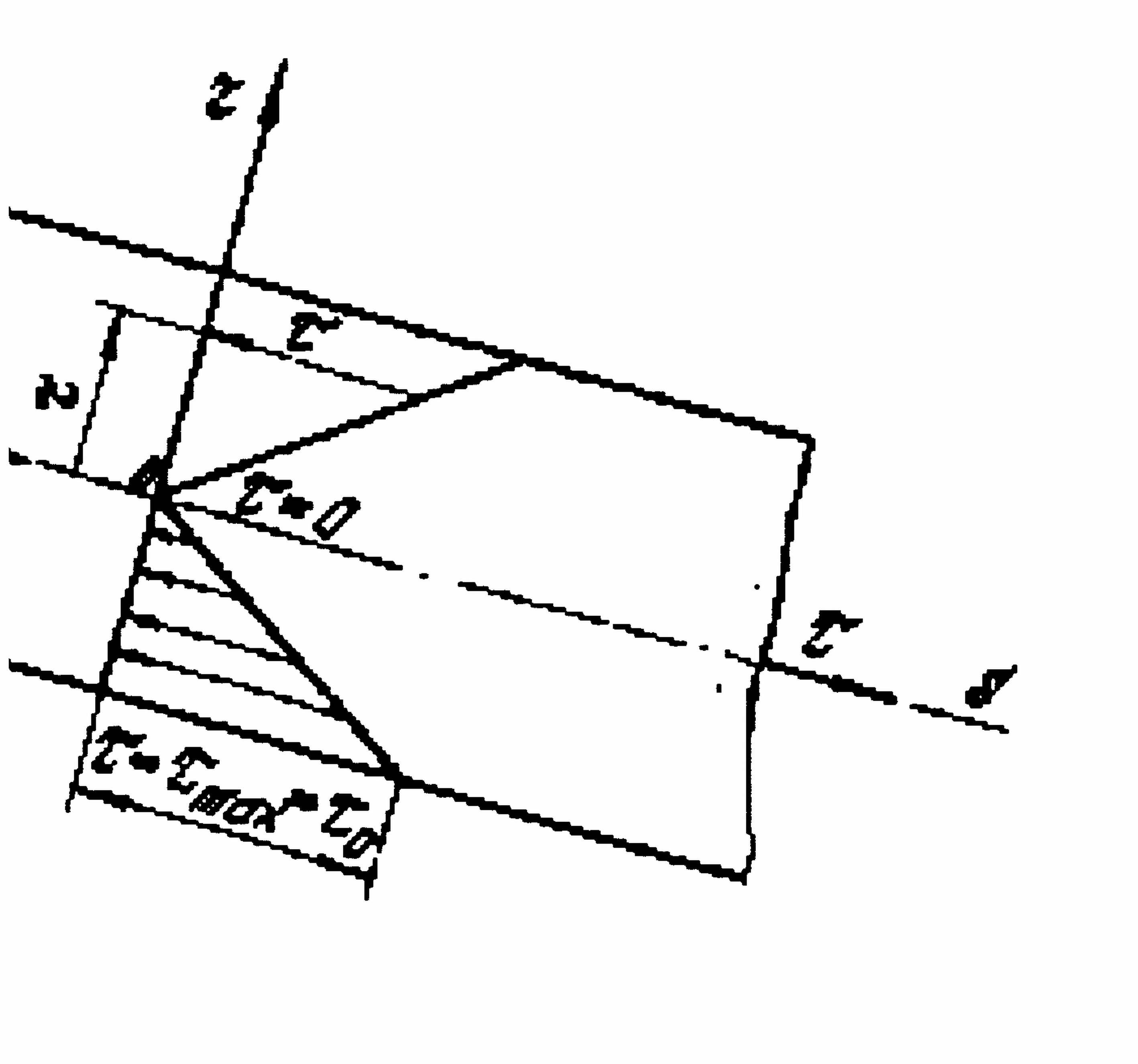
Рис.4

Уравнение (5.10) представляет собой общее выражение потерь напора при равномерном движении жидкости в трубопроводах круглого сечения.

В гидродинамике вместо касательного напряжения употребляют величину

, (5.16)

где С_f –коэффициент местного трения; –средняя скорость течения.

Подставляя в формулу (5.15) вместо его значение из формулы (5.16), получим

(5.17)

Эта формула известна в литературе как формула Дарси-Вейсбаха.

Обозначив , получим

(5.18)

где d –диаметр трубы.

Величина имеет размерность квадрата скорости. Если ввести обозначение где –скорость касательного напряжения на стенке, или динамическая скорость, то уравнение (5.16) можно представить в виде

(5.19)

Коэффициент , называемый коэффициентом гидравлического трения, имеет, очевидно, тот же смысл, что и . Важно выяснить, от каких параметров и как именно зависят эти коэффициенты.

Приведенный метод можно использовать также для определения вида формулы потерь напора на местные сопротивления. В этом случае, учитывая, что местные потери практически не зависят ни от длины участка трубы, ни от её диаметра, можно получить формулу

(5.20)

где –безразмерный коэффициент, так называемый коэффициент местных потерь; –средняя скорость потока после прохода через местное сопротивление.

Эта формула известна в литературе как формула Вейсбаха для местных сопротивлений.

Заметим, что к этому виду можно привести и формулу (18), если обозначить

. (5.21)

Тогда

.

Формула (5.20) применима для всех видов гидравлических сопротивлений, причем коэффициент сопротивления (или ) в наиболее общем случае зависит от конфигурации потока и числа Рейнольдса, Установление конкретного вида этих зависимостей в основном опирается на экспериментальные данные.