5.2. Режимы движения жидкости. Число Рейнольдса
Эксперементально установлено, что движение жидкости в трубах, каналах, порах грунта и т.д. может происходить при двух различных режимах: ламинарном и турбулентном.
Ламинарный режим характеризуется струйчатым упорядоченным движением, при котором отдельные струйки жидкости не перемешиваются между собой.
При турбулентном режиме, наряду с общим поступательным движением потока (например, в трубе), частицы жидкости совершают хаотическое, неупорядоченное перемещение, в результате чего наблюдается интенсивное перемешивание жидкости.
Многочисленные
опыты показывают, что переход от
ламинарного режима течения к турбулентному
происходит при определенной средней
скорости
,
называемой критической. Однако величина
этой скорости различна для труб разных
диаметров и для различного рода жидкостей.
Вместе с тем исследованиями было
установлено, что режим течения жидкости
определяется величиной безразмерного
критерия (числа), учитывающего основные
факторы этого движения: среднюю скорость
, диаметр трубы
d,
плотность жидкости
и её абсолютную вязкость, характеризуемую
динамическим коэффициентом вязкости
.
Этим критерием является число Рейнольдса
Re,
выражение для определения которого
имеет вид
,
(5.2)
где
–кинематический коэффициент вязкости.
Необходимо иметь
в виду, что в формуле (5.2) диаметр d
может быть заменен любым линейным
параметром
,
характеризующим живое сечение потока,
в частности гидравлическим радиусом
R,
т.е. формулу (5.2) можно записать в виде
(5.3)
Формулой (5.3) пользуются, когда живое сечение потока не является круглым, например, при движении жидкости в открытых каналах, в том числе в круглой трубе, работающей неполным сечением.
Значение числа
Рейнольдса, при котором происходит
переход от ламинарного режима течения
к турбулентному, т.е. отвечающее
критической скорости
,
называется критическим и обозначается
символом
.
Величина
не зависит от
рода жидкости и размеров живого сечения
потока. Опытами установлено, что
критическое число Рейнольдса, подсчитанное
по формуле (5.2), равно
а по формуле (5.3) –
,
так как
.
При
режим движения является турбулентным,
при
–ламинарным.
С физической точки зрения число Рейнольдса представляет собой отношение кинетической энергии рассматриваемого объема жидкости к работе сил трения, обусловленных вязкостью жидкости.
Кинетическая
энергия тела зависит от его объема и
пропорциональна
,
где
–линейные
размеры рассматриваемого объема
жидкости. Работа сил трения зависит от
размеров поверхности рассматриваемого
объема жидкости и пропорциональна
.
Отношение кинетической энергии объема жидкости к работе сил трения будет равно:
.
Чем меньше число Рейнольдса, тем большую роль играют силы вязкости.
5.3. Характер зависимости потерь напора
от средней скорости течения жидкости
в круглой цилиндрической трубе
Экспериментальными исследованиями установлено, что при ламинарном режиме движения зависимость потери напора от средней скорости течения имеет линейный характер:
(5.4)
а при турбулентном режиме движения
(4.5)
где показатель
степени
и
–коэффициенты пропорциональности
соответственно для ламинарного и
турбулентного режимов, зависящие от
рода жидкости (её плотности
и вязкости
),
формы и размеров живого сечения. Кроме
того, коэффициент
зависит еще и от шероховатости смоченной
поверхности. Характер зависимости
потерь напора от средней скорости
показан на рис. 1.
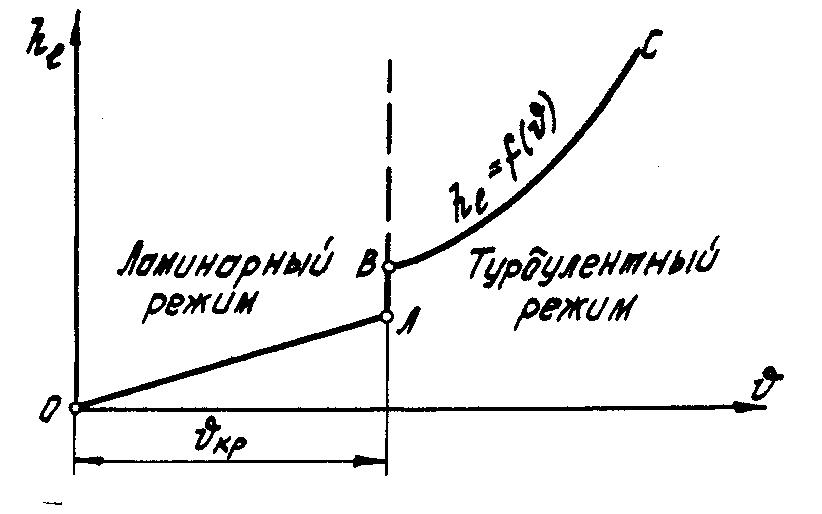
Рис.1
Ламинарному режиму
отвечает прямая ОА. Точка А соответствует
критической скорости
,
т.е. переходу потока из ламинарного
режима в турбулентный. От точки В
и далее с увеличением скорости имеет
место устойчивое турбулентное движение,
которому соответствует кривая ВС.
Численные значения
коэффициентов
и
,
а также показателя степени m
определяются опытным путем с помощью
графика зависимости потерь напора по
длине
от средней скорости
,
построенного в логарифмических
координатах (рис. 2).
Для ламинарного движения:
.
Здесь переменными
будут
и
,
.
Таким образом, получили уравнение
прямой.