4.11. Гидравлический и пьезометрический уклоны

Для характеристики относительного изменения полного напора по длине потока введем понятие о гидравлическом уклоне.

Среднее значение гидравлического уклона на участке потока между сечениями 1–1 и 2–2 (рис.6) определяется как отношение потери напора к длине участка:

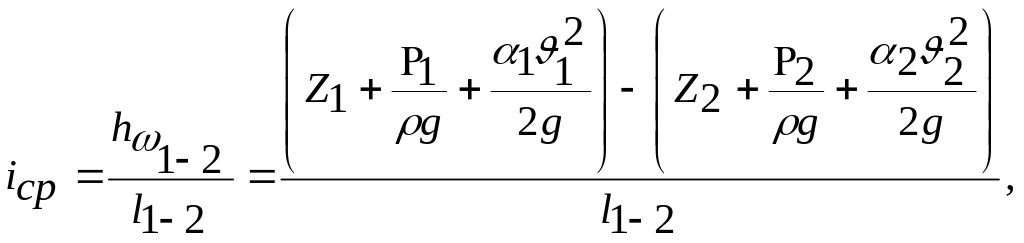
где − расстояние (по пути движение потока жидкости) между сечениями 1–1 и 2–2.

Гидравлический уклон −величина безразмерная и всегда больше нуля. В общем случае величина гидравлического уклона по длине потока переменная и в данном сечении потока определяется выражением

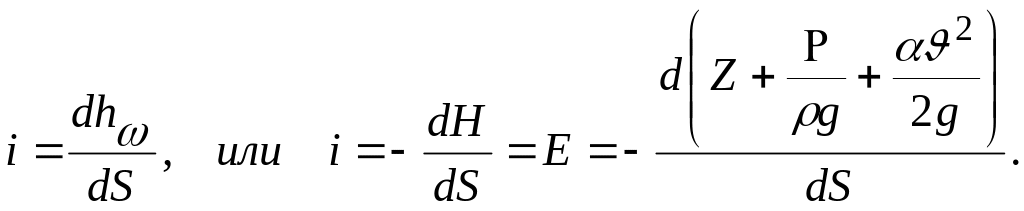
Здесь знак «минус» указывает на убывание полного напора по пути движения жидкости.

Понятие об уклоне можно ввести и для пьезометрической линии.

Средний пьезометрический уклон определяется по формуле

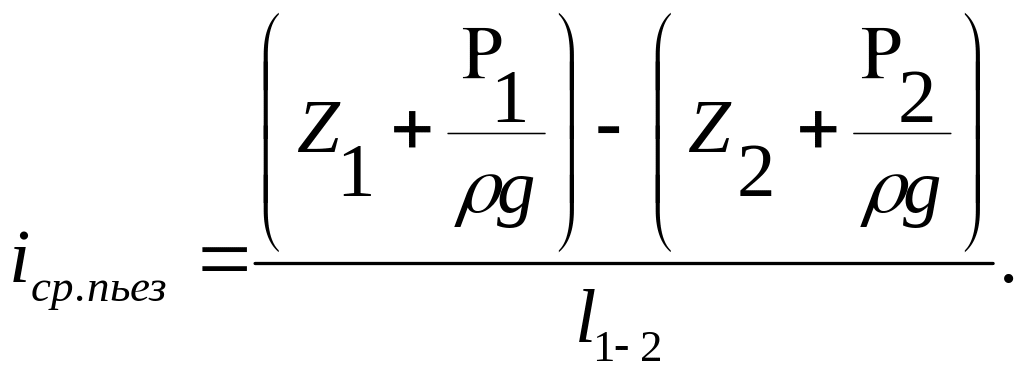
Значение пьезометрического уклона для некоторого сечения потока определяется выражением

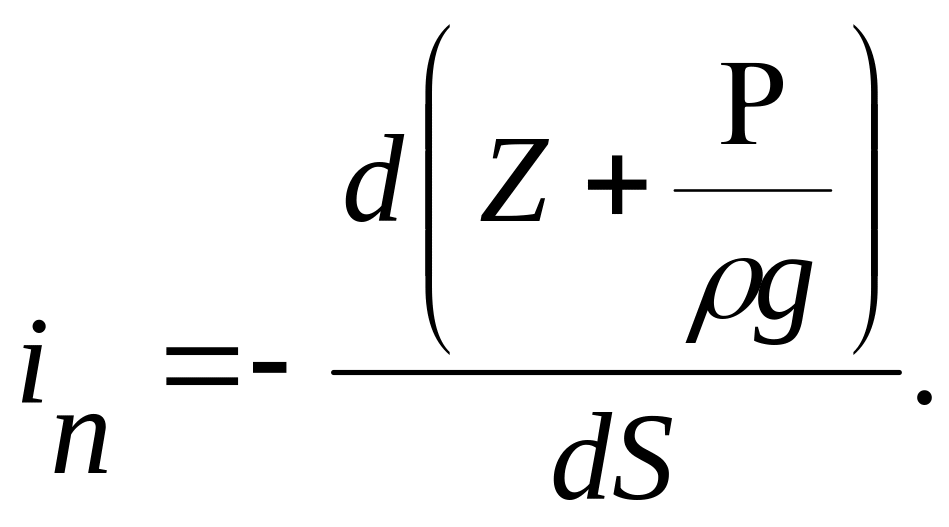
Пьезометрический уклон может быть положительным, равным нулю и отрицательным

В случае, изображенном на рис. 4, пьезометрический уклон отрицательный, а на рис. 6 – положительный.

Глава пятая

Гидравлические сопротивления

5.1. Понятие о гидравлических сопротивлениях

Для практического использования уравнения Бернулли (4.40) необходимо установить способ определения величины потерь напора , вызванных действием в потоке сил сопротивления.

Как показывают многочисленные эксперименты, механизм действия сил сопротивления существенно различен при разных граничных условиях и разных режимах движения жидкости.

Все гидравлические сопротивления удобно разделить на два класса или вида, сущность которых поясним на примерах.

Опыт показывает, что при ламинарном установившемся течении жидкости в круглой горизонтальной цилиндрической трубе имеет место потеря напора, равномерно распределенная по длине потока и равная падению пьезометрической линии на рассматриваемом участке. Здесь мы встречаемся с потерями по длине, обусловленными силами трения частиц жидкости друг о друга и о стенки трубы. Обозначим их .

С другим видом потерь мы встречаемся в случаях резких изменений формы граничных поверхностей потока на коротком участке. Так, например, при протекании жидкости через диафрагму можно наблюдать достаточно резкое падение линии энергии на относительно коротком участке, потери на котором в несколько раз превышают потери в равномерном потоке на участке той же длины. В данном случае внешним фактором, который вызывает увеличение потерь, является деформация потока пограничными поверхностями, сопровождающаяся перестройкой закона распределения скоростей и образованием зон, заполненных вихревыми массами жидкости. Такие участки резких деформаций потока называют местными гидравлическими сопротивлениями, а вызванные ими потери – местными потерями энергии, которые обозначим .

Наряду с различием конфигураций граничных поверхностей необходимо учитывать влияние режимов движения жидкости на величину и механизм потерь. Для оценки потерь важно знать условия перехода ламинарного течения в турбулентное.

В реальных конструкциях участки равномерного движения жидкости могут чередоваться с местными сопротивлениями. При подсчетах полных потерь напора широко применяется принцип сложения, согласно которому полные потери равны сумме потерь на отдельных участках равномерного движения и потерь на всех местных сопротивлениях:

(5.1)

где –потеря по длине на i–м участке равномерного движения; - местная потеря на i–м местном сопротивлении.

При протекании через местное сопротивление в потоке возникают деформации эпюры скоростей, отрывы и вихревые зоны, которые могут распространяться как вверх, так и вниз по течению. В связи с этим, если величины вычисляют по формулам, установленным для изолированных местных сопротивлений, то применение принципа сложения потерь согласно (5.1) будет правомерным лишь в том случае, когда местные сопротивления не влияют друг на друга, т.е. разделены участками движения со стабилизированным распределением скорости. В противном случае два или более местных сопротивления следует рассматривать как одно сложное, и для него должны быть установлены специальные расчетные зависимости.

Как указано выше, структура потока и механизм потерь в местных сопротивлениях и на участках равномерного движения существенного различны, а поэтому требуют установления частных зависимостей, пригодных для сопротивлений данного типа.