4.9. Уравнение д. Бернулли

для струйки реальной жидкости

Напишем уравнения Навье-Стокса в развернутом виде, ограничиваясь рассмотрением только установившегося движения:

(4.29)

С учетом того что для всех точек оси струйки

преобразуем первое уравнение системы (4.29) следующим образом:

или

Аналогично второе и третье уравнения системы (4.29) можно привести к виду

;

.

Пусть объемные силы, действующие на жидкость, имеют потенциал:

Сложив полученные уравнения и сгруппировав слагаемые соответствующим образом, получим

. (4.30)

В правой части уравнения (4.30) второе слагаемое выражает работу, затраченную на преодоление сил вязкости при перемещении единицы массы жидкости на расстояние dS. Перепишем уравнение (4.30) в виде

(4.31)

Интегрируя выражение (4.31) на участке между сечениями 1-1 и 2-2 длиной S по оси струйки, получим

или

(4.32)

где

Уравнение (4.32) и является уравнением Д. Бернулли для струйки реальной жидкости.

Величина A является энергией, потерянной единицей массы жидкости на участке между сечениями 1-1 и 2-2. Теоретически определить величину в общем случае чрезвычайно трудно вследствие сложности интегрирования уравнения Навье-Стокса.

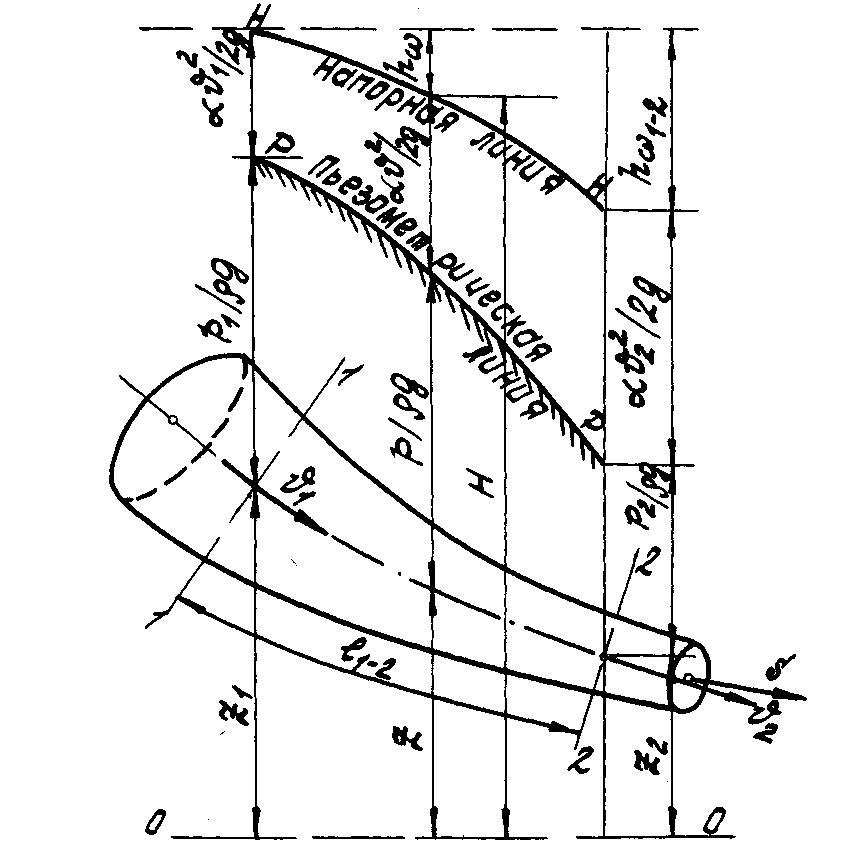
Обозначая потерянную работу, совершаемую единицей веса жидкости против сил сопротивления при перемещении её из сечения 1-1 в сечение 2–2 (рис.4), через и допуская, что П= -gZ, уравнение (4.32) можно представить в виде

. (4.33)

Как видим, в случае реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению движения. В соответствии с этим график уравнения Бернулли для струйки реальной жидкости (рис.4) будет отличаться от аналогичного графика для идеальной жидкости.

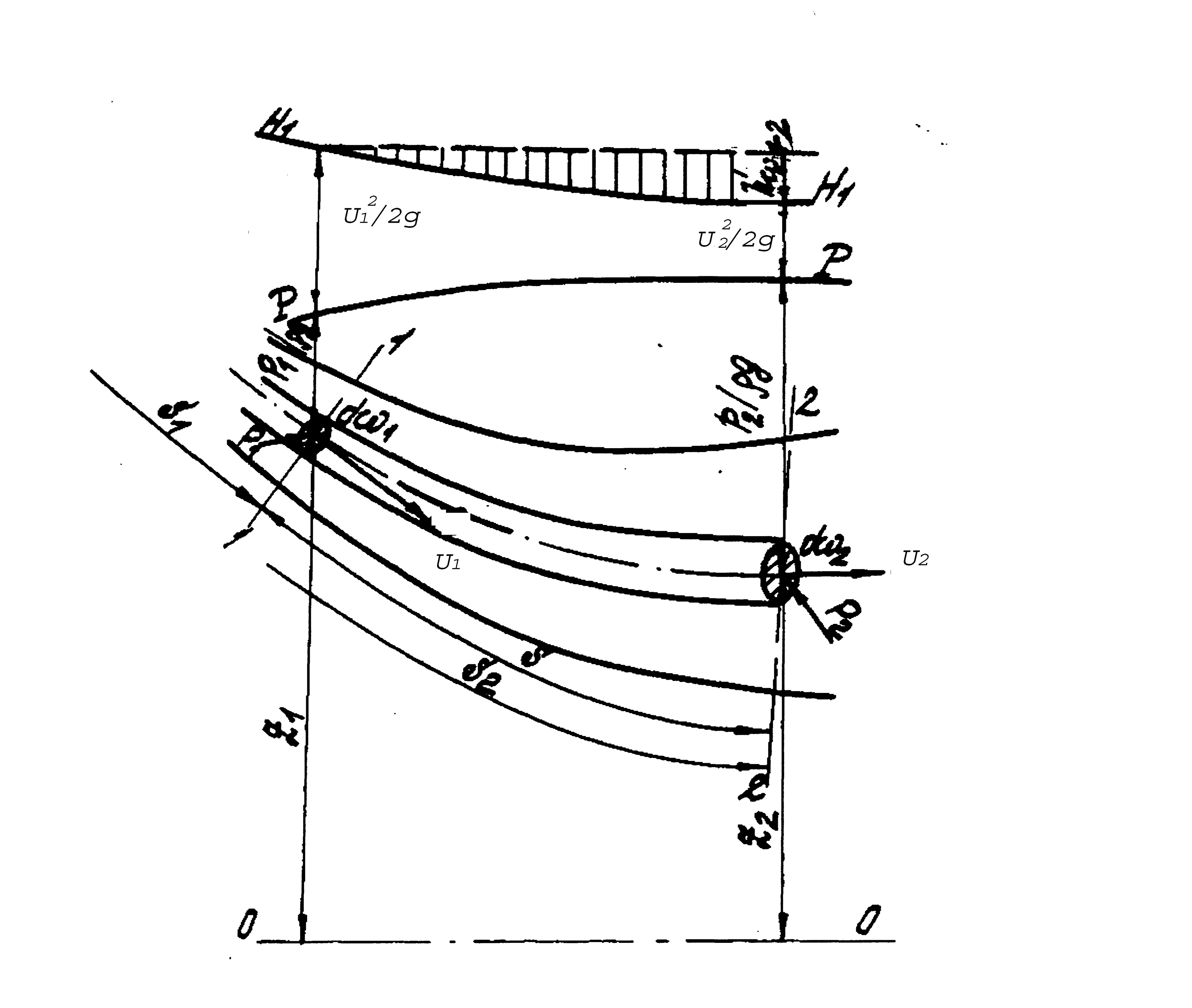
Рис. 4

4.10. Уравнение д. Бернулли

для потока реальной жидкости

Рассмотрим основные свойства плавно изменяющихся потоков. Для этого выберем в живом сечении mn систему координат X, Y, Z, направив ось X вдоль оси потока (рис.5), а ось Y – горизонтально.

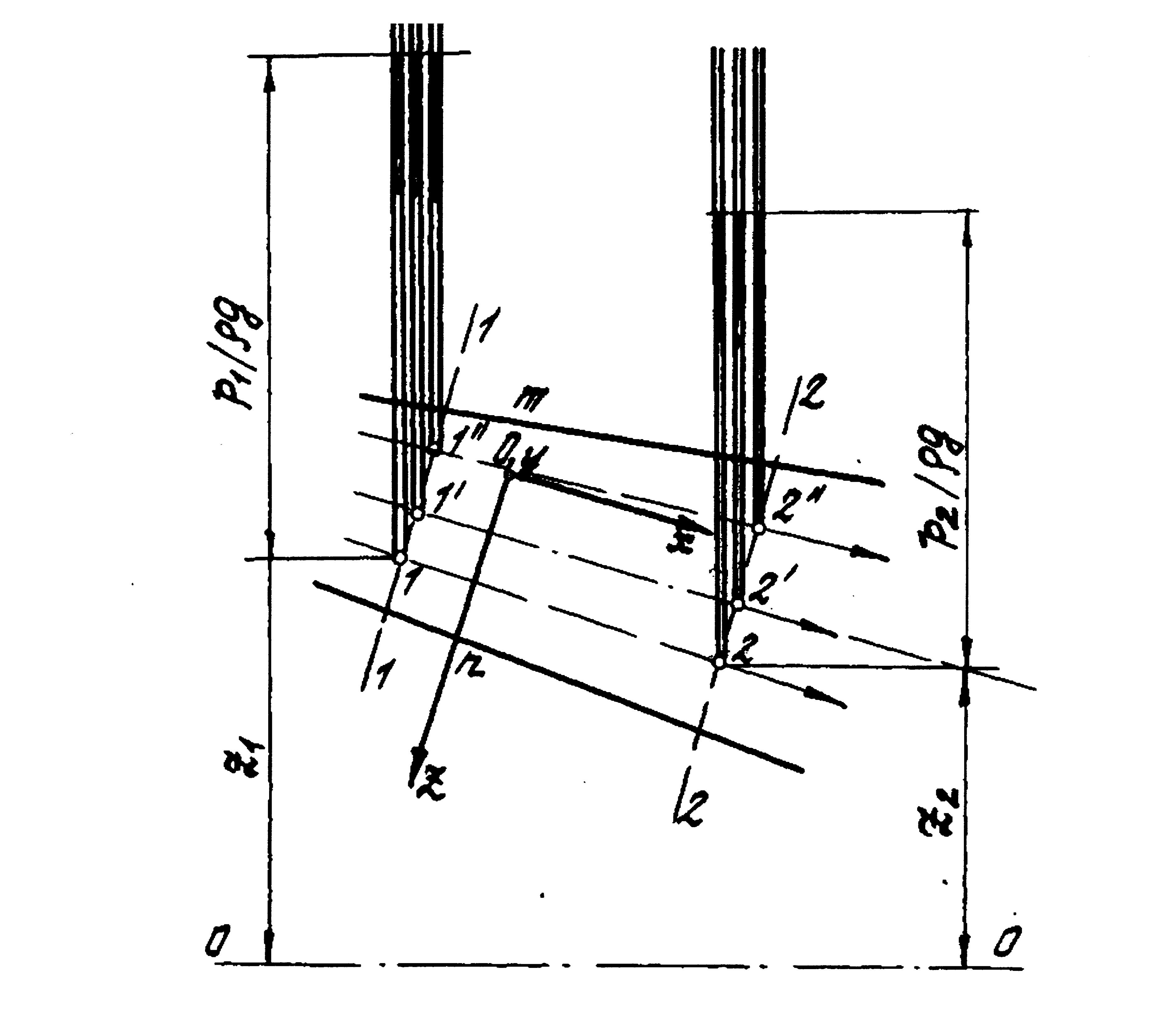
Рис. 5

Поскольку в рассматриваемом потоке углы, образованные линиями

тока, малы, то при выбранной системе координат поперечные компоненты скорости малы и можно принять, что Тогда в уравнениях Навье-Стокса для установившегося движения можно пренебречь членами, зависящими от этих компонентов, после чего получим

(4.34)

Из дифференциального уравнения неразрывности вытекает, что тогда уравнения (4.29) запишутся в виде

(4.35)

Так как последние два уравнения системы (4.35) ничем не отличаются от соответствующих двух дифференциальных уравнений равновесия жидкости, можно заключить, что при плавно изменяющемся движении в пределах живого сечения потока давление распределяется по гидростатическому закону.

При плавно изменяющемся движении в плоскостях, параллельных плоскости YOZ для различных точек данного живого сечения, величины Z и имеют разное значение, однако их сумма постоянна:

(4.36)

В другом живом сечении сумма будет иная, но постоянная для всех точек этого сечения. Этот результат позволяет распространить уравнение Бернулли на поток конечных размеров.

Соблюдая условие плавной изменяемости, при переходе к потоку жидкости будем исходить из уравнения (4.33). Умножим все члены этого уравнения на (весовой расход струйки), получим уравнение, выражающее энергию отдельной элементарной струйки:

. (4.37)

Просуммировав энергии струек для живого сечения потока жидкости, получим энергию всего потока:

(4.38)

Рассмотрим каждый из членов этого уравнения в отдельности.

Слагаемые

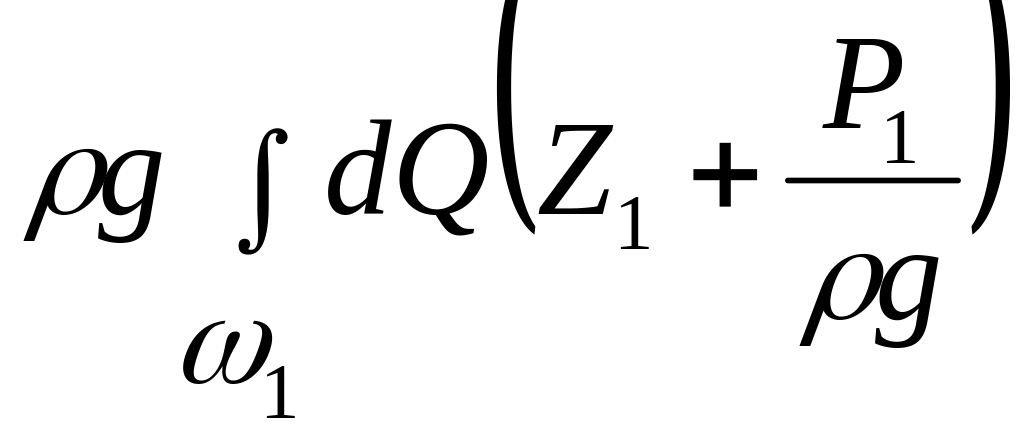и

выражают потенциальную энергию потока жидкости в сечениях 1-1 и 2-2, которой обладает масса жидкости, проходящая через живое сечение потока в единицу времени.

С учетом замечания о плавной изменяемости движения потенциальная энергия для произвольного сечения может быть определена следующим образом:

.

Слагаемые

и

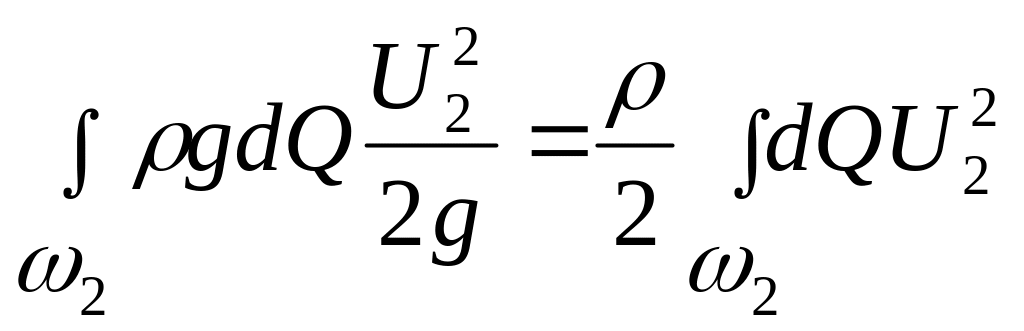
выражают кинетическую энергию массы жидкости, протекающей через живые сечения 1–1 и 2–2 потока в единицу времени. Рассмотрим эти слагаемые более подробно. Так как для произвольного сечения струйки

, то

Местную скорость U можно представить в виде:

где U −средняя скорость; а −разность между местной и средней скоростями . Сделав подстановку, получим:

или

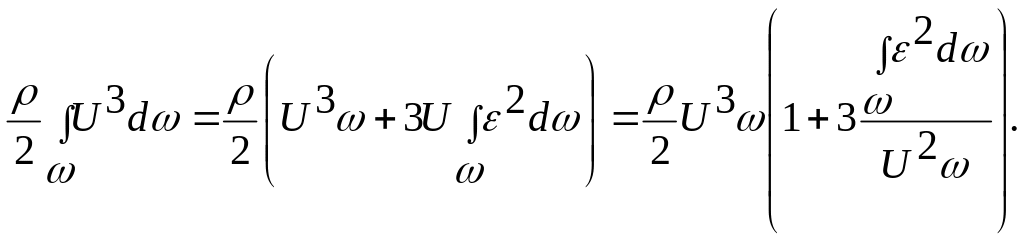
Здесь учтено, что так как

Интеграл так как малая величина для разных точек сечения имеет различный знак.

Обозначим для краткости , получим выражение для кинетической энергии потока жидкости:

из которого видно, что поправочный коэффициент , называемый коэффициентом Кориолиса, или коррективом кинетической энергии, представляет собой отношение действительной кинетической энергии потока жидкости, протекающей через поперечное сечение потока в единицу времени, к кинетической энергии, которая имела бы место при этом же расходе, если бы все частицы жидкости обладали одинаковыми скоростями, равными средней скорости, т.е.

.

Величина этого коэффициента всегда больше единицы и зависит от степени неравномерности распределения скорости по сечению: для развитого ламинарного течения в круглой цилиндрической трубе − 2, а для турбулентного − , однако при значительной неравномерности эпюры скорости может достигать больших значений.

Последнее слагаемое , выражающее потерянную энергию потока жидкости за единицу времени при перемещении его из сечения 1–1 в сечение 2–2, можно представить в виде

.

Подставляя полученные выражения для слагаемых в уравнение (4.38), будем иметь:

,

или после сокращения на

, (4.39)

или

. (4.40)

В последнем виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной вязкой несжимаемой капельной жидкости при установившемся плавно изменяющемся движении.

Как следует из вывода уравнения (4.40), выполнение условий плавной изменяемости необходимо лишь для выбранных расчетных сечений, тогда как на участке между этими сечениями они могут нарушаться.

Согласно выполненным преобразованиям четвертый член правой части уравнения (4.40) выражает усредненную потерю удельной механической энергии между сечениями 1–1 и 2–2.

Уравнению (4.40) может быть дана геометрическая трактовка. Так, учитывая, что все члены имеют линейную размерность, можно построить график уравнения Бернулли для потока вязкой жидкости (рис.6).

Рис. 6