4.4. Интегралы уравнения движения жидкости

Уравнения Эйлера для общего случая не интегрируются. Интегрирование возможно только в некоторых частных случаях при упрощающих предположениях. В зависимости от принятых допущений различают несколько случаев прямого интегрирования:

1. Интеграл Лагранжа-Коши для безвихревого неустановившегося движения.

2. Интеграл Л. Эйлера для безвихревого установившегося движения.

3. Интеграл Д. Бернулли для установившегося движения вдоль линии тока.

Все интегралы получены при условии, что массовые силы потенциальны.

4.5. Интеграл Лагранжа-Коши

для безвихревого неустановившегося движения

Приведем уравнения движения идеальной жидкости (4.6) к виду, позволяющему из всех возможных типов движения выделить группу потенциальных потоков.

Напишем выражение для полной скорости U через её проекции:

.

Взяв частную производную от этого выражения по x, находим

.

Вычитая соответственно из левой и правой частей первого из системы уравнений (2) выражение для частной производной по x, получим

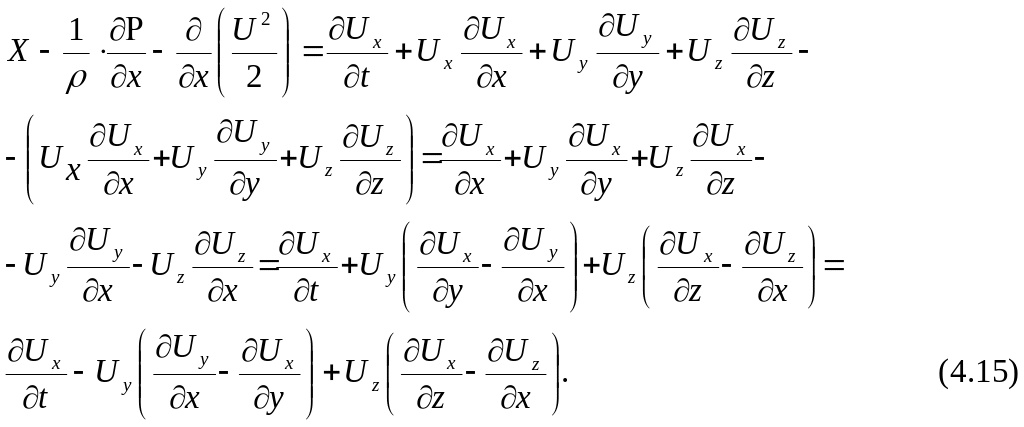
Выражения в скобках в правой части уравнения (4.15) равны удвоенным компонентам угловой скорости соответственно по осям OY и OZ (см. 3.7, уравнения 3.24), т.е.

.

С учетом этого из формулы (3) получим

.

Аналогичные уравнения можно написать и для осей OY и OZ:

;

.

В результате получим следующую систему уравнений:

(4.16)

Записанные в таком виде уравнения Эйлера, т.е. в форме предложений И.С. Громеко, позволяют отделить вихревые движения от безвихревых.

Для безвихревого (потенциального) движения компоненты угловой скорости, каждый в отдельности, равны нулю: , поэтому уравнения Эйлера для потенциального движения примут вид

(4.17)

Пусть объемные силы имеют потенциал, тогда проекции ускорения объемных сил X, Y и Z определяются выражениями:

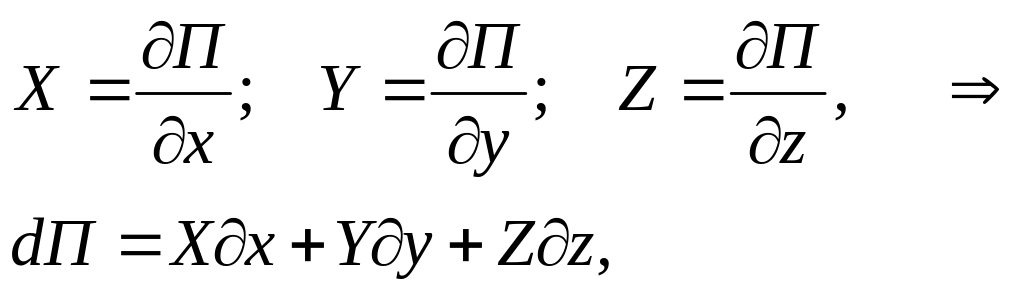
где П –силовая функция.

Рассмотрим далее производные Так как движение потенциальное, то существует функция , для которой

Поэтому

.

По аналогии

; .

С учетом вышеизложенного можно, например, первое уравнение системы (4.17) привести к виду

.

Аналогичные уравнения можно написать и для осей OY и OZ. В результате получим систему уравнений:

Предполагая жидкость однородной и несжимаемой, после умножения этих уравнений соответственно на независимые величины dx, dy, dz и их сложения, найдем

,

или

(4.18)

Полученный интеграл называется интегралом Лагранжа-Коши. Здесь временная постоянная c(t) одинакова для всех точек рассматриваемого объема и может быть определена, если в какой-нибудь точке поля известна функция .

В частном случае, когда движение установившееся ( ),

. (4.19)

Здесь постоянная не зависит от времени и одинакова для всех точек рассматриваемого объема.

4.6. Интеграл л. Эйлера

для безвихревого установившегося движения

Рассмотрим установившееся потенциальное движение несжимаемой жидкости в поле силы тяжести. В этом случае П=-gZ и .

Подставляя в уравнение (4.15) вместо П его значение, найдем

(4.20)

или, деля на g, получим:

(4.21)

Это выражение и называется интегралом Л. Эйлера.