Глава четвертая основные уравнения гидродинамики

4.1. Основные дифференциальные уравнения движения

невязкой жидкости

В потоке жидкости рассмотрим движение элементарного объема в форме параллелепипеда со сторонами dx,dy,dz (рис. 1).

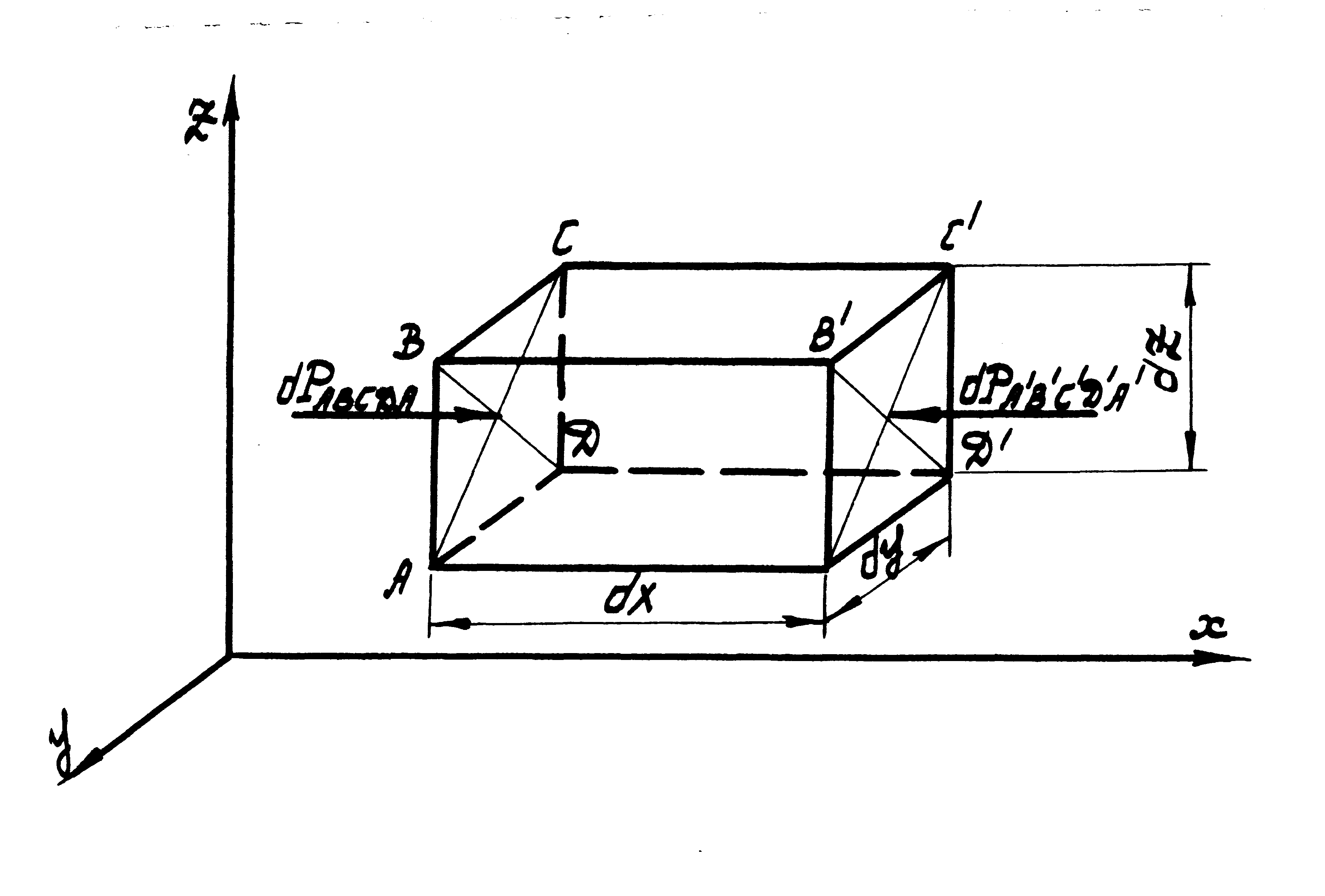
Рис. 1

Напишем второй закон Ньютона для массы жидкости в этом объеме сначала в проекциях на ось Ox:

(4.1)

где масса , а проекция ускорения

.

Определим проекцию на ось Ox равнодействующих внешних сил. Проекция силы давления на боковую грань АВСД

dP_АВСДА=p·dy·dZ,

где p − среднее давление в пределах указанной грани.

Среднее давление в пределах грани

Следовательно, сила давления на эту грань

С учетом того что проекция на ось OX силы давления на другие грани параллелепипеда равна нулю, сумма проекций сил давления на боковые грани АВСД и будет равна

Проекция объемных сил на ось Ox можно представить в виде

где X –проекция ускорения на ось OX.

Подставляя выражение для проекций сил в формулу (1), получим

или после сокращения на , т.е. отнеся все члены уравнения к единице массы жидкости в рассматриваемом объеме,

Аналогичные уравнения можно написать и для других координатных осей. В результате получим следующую систему уравнений

(4.2)

которая называется системой уравнений Л.Эйлера для движения сплошной среды.

В систему из трех уравнений входят четыре неизвестные функции:U_X,U_Y,U_Z и p. Поэтому для ее решения необходимо иметь еще одно уравнение, которое связало бы между собой названные функции. Таким уравнением является рассмотренное выше уравнение неразрывности (3.15).

4.2. Дифференциальные уравнения движения

вязкой жидкости (уравнения Навье-Стокса)

Дифференциальные уравнения движения вязкой жидкости могут быть составлены путем дополнения уравнений Л.Эйлера слагаемыми, учитывающими вязкость жидкости. Тогда уравнения Эйлера запишутся в виде

(4.3)

где F_x ,F_y, и F_z −проекции сил вязкости, отнесенные к единице массы жидкости, на координатные оси. Найдем силы F_x ,F_y и F_z , предполагая, что жидкость движется слоями, т.е. без перемешивания. Под действием сил вязкости возникают как тангенциальные, так и нормальные напряжения.

Выделим элемент движущейся жидкости в форме параллелепипеда с ребрами, параллельными координатным осям, и определим сумму проекций сил вязкости, действующих только на те три грани параллелепипеда, которые образуют трехгранный угол с вершиной А (рис. 2).

Рис.2

Для удобства дальнейших рассуждений введем двойную индексацию напряжения, например: для нормального напряжения − р_хх, касательного напряжения − и т.д. Здесь первый индекс указывает на то, что площадка, для которой определяется напряжение, расположена нормально к данной оси координат, а второй –направление действия напряжения. С учетом этого получим выражение для проекций сил, действующих на грани трехгранного угла с вершиной А:

ось ОХ ; ; ;

ось ОY ; ; ;

ось ОZ ; ; .

Переходя затем к проекциям сил, действующих на грани трехгранного угла с вершиной С, отметим, что напряжения на этих гранях будут отличаться от напряжений на гранях трехгранного угла с вершиной А.

Итак, выражения для проекций сил, действующих на грани трехгранного угла с вершиной С:

ось ОХ ; ; ;

ось ОY ; ; ;

ось ОZ ; ; ;

где для оси OX

Аналогичные уравнения можно получить и для двух других осей координат.

Составим теперь уравнение для силы, представляющей собой сумму проекций на ось OX сил вязкости.

Полагая, что направление сил, действующих на грани угла с вершиной , противоположно направлению сил, действующих на грани трехгранного угла с вершиной А, получим

Но

в силу чего, делая соответствующую подстановку, найдем

Сила F_x, входящая в уравнение Эйлера, как указано выше, представляет собой проекцию силы вязкости, отнесенной к единице массы жидкости, т.е. где в данном случае а поэтому для силы F_x получим выражение

(4.4)

где р_хх −нормальные, и касательные напряжения.

Касательные напряжения в пределах грани dxdy остаются одинаковыми для всех ее точек, т.е. не зависят от координат X и Y и изменяются только при перемешивании этой грани вдоль оси OY, т.е. зависят от координаты Y.

Другими словами, −это касательные напряжения, зависящие только от градиента скорости Поэтому в соответствии с законом внутреннего трения в жидкости Ньютона а (по аналогии).

Рассмотрим производную . Здесь P_xx представляет собой нормальное к площадке dydz напряжение, обусловленное влиянием вязкости (сжатие в условиях торможения и растяжение при ускоренном движении). Поэтому можно допустить, что напряжение P_xx может также определяться по закону Ньютона , тогда

Делая соответствующие подставки в уравнение (4.4), получим

,

или, так как

Аналогично для других координатных осей можно записать

Вводя теперь полученные выражения для сил F_x,F_y,F_z в систему уравнений (4.3), после некоторой перестановки слагаемых получим дифференциальные уравнения движения вязкой жидкости:

(4.5)

или окончательно

(4.6)

где −оператор Лапласа.

Эти уравнения именуются уравнениями Навье-Стокса. Они составляют основу гидродинамики реальной жидкости.

При решении конкретных задач о движении несжимаемой жидкости к уравнениям Навье-Стокса необходимо добавить уравнение неразрывности в форме

Таким образом, мы получаем замкнутую систему четырех уравнений, достаточную для определения четырех неизвестных величин: трех компонентов скорости U_x,U_y,U_z и давления P.

Кроме того, для определения произвольных постоянных и произвольных функций, появляющихся при интегрировании, должны быть сформулированы так называемые краевые условия, т.е. начальные и граничные условия.

Начальные условия, о которых может идти речь лишь в случае не стационарного движения, указываются посредством задания поля скоростей и давлений в какой-нибудь определенный (начальный) момент времени t=t_x.

Задание граничных условий для случая движения вязкости жидкости сводится к признанию того факта, что частицы жидкости, непосредственно соприкасающиеся с поверхностью твердого тела, прилипают к ней и поэтому имеют одинаковую с ней скорость.

В частном случае при обтекании неподвижного тела граничное условие для скорости вязкой жидкости должно быть записано в виде V = 0.

Дифференциальные уравнения движения реальной жидкости представляют собой нелинейные уравнения второй степени в частных производных. В самом общем виде эти уравнения не могут быть проинтегрированы. Их решение возможно лишь для частных случаев, допускающих упрощение этих уравнений путем отбрасывания тех или иных членов. Уравнения движения критериев гидродинамического подобия будут рассмотрены ниже.