3.6. Вихревые и безвихревые движения

Частица жидкости при движении может изменять форму, т.е. де­формироваться. Поэтому движение частицы может быть разложено на поступательное, вращательное и деформационное.

На примере параллелепипеда (рис.5), схематически показаны: поступательное и вращательное; поступательное и деформационное, а также комбинированное (поступательное, вращательное и деформационное движения).

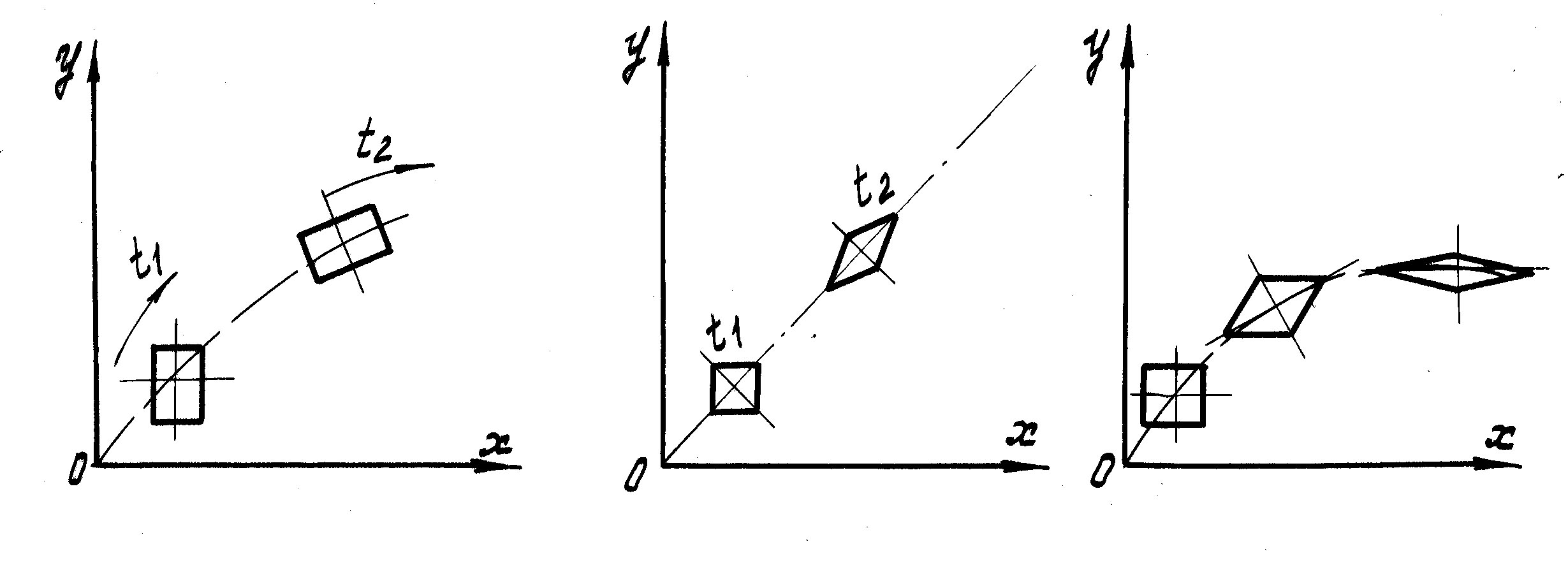
Рис.5

Как видно из схем, вращательное движение характеризуется пово­ротом параллелепипеда вокруг его центра, причем диагонали паралле­лепипеда изменяют свое положение относительно координатных осей. Вращение частицы можно оценивать величиной и направлением угловой скорости при её повороте.

Деформационное движение характеризуется изменением углов между гранями параллелепипеда и оценивается скоростью изменения этих углов.

3.7 Уравнение компонентов вихря

Вектор угловой скорости вращения частицы жидкости называется вихрем.

Рассмотрим движение частицы жидкости, имеющей первоначально форму кубика с ребрами, параллельными координатным осям. На (рис.6) этот кубик изображен в проекции на плоскость XOZ квадратом МАСВ.

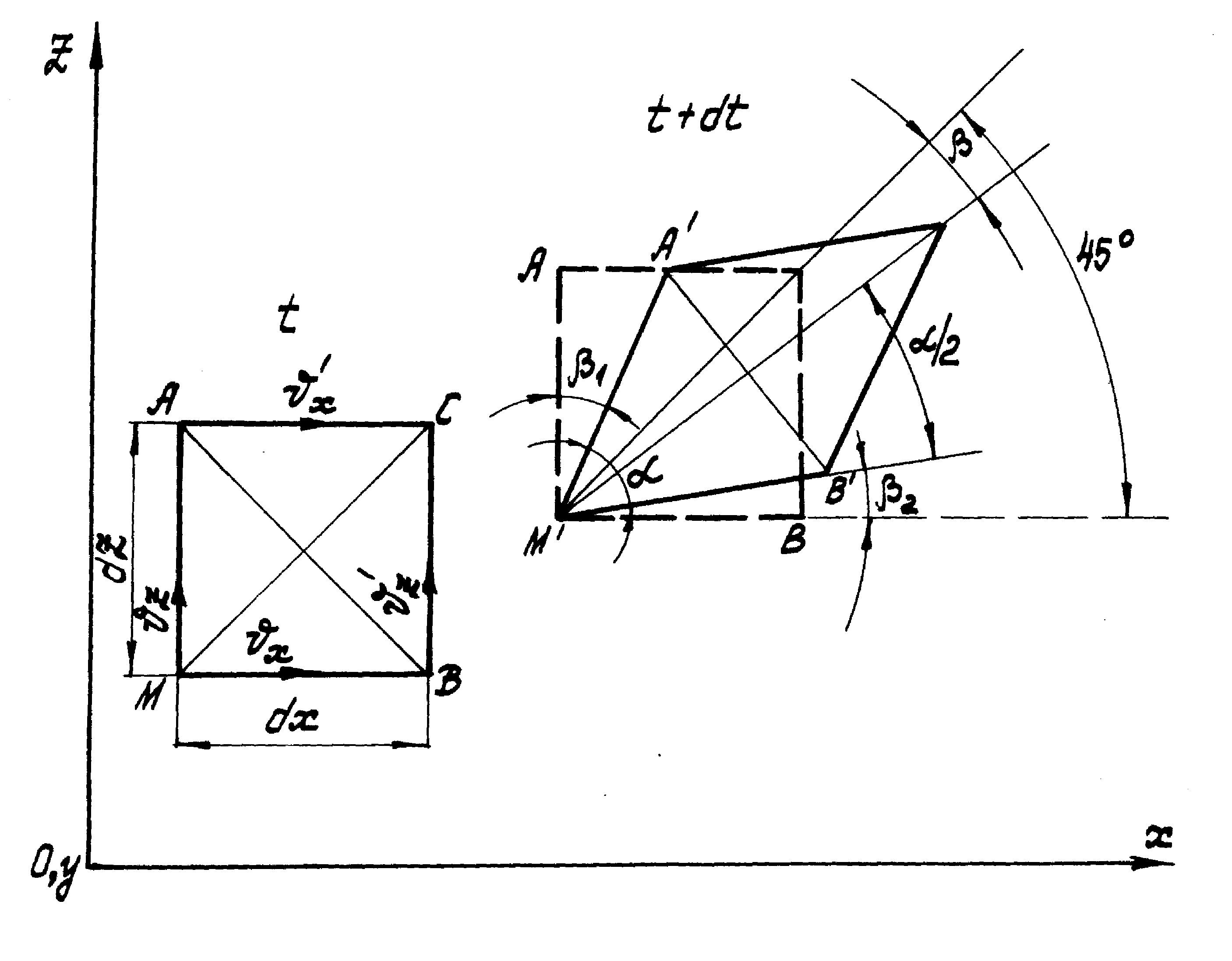
Рис.6

Пусть за время dt кубик переместился и его проекцией стала, фигура Диагональ МС при этом переместилась в положение , изменив свое начальное направление на угол . Скорость этого поворота и представляет собой угловую скорость вращения относительно координатной оси Oy, то есть проекцию вихря.

Найдем выражение угла поворота . Из (рис.6) следует, что

.

Угол , поэтому

.

Принимая и (что допустимо по малости углов), получим

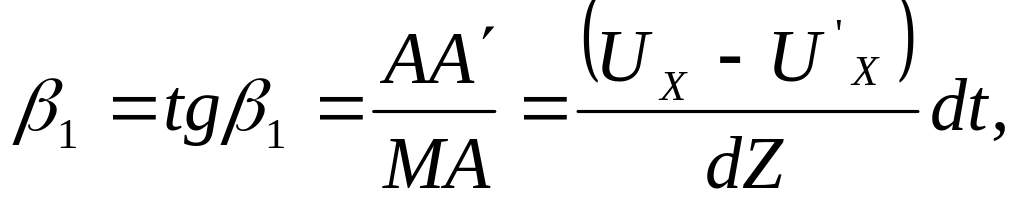
где U_X и − соответственно проекции на ось Ox скоростей точек М и А.

Но поэтому

тогда

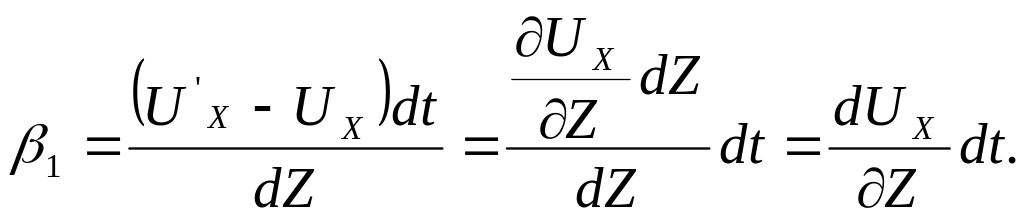
Аналогично получим

следовательно,

Отсюда компонент вихря – угловая скорость вращения вокруг оси OY

Проводя аналогичные рассуждения по отношению к углам поворота вокруг двух других координатных осей, можно получить следующие выражения для проекций вихря на три оси:

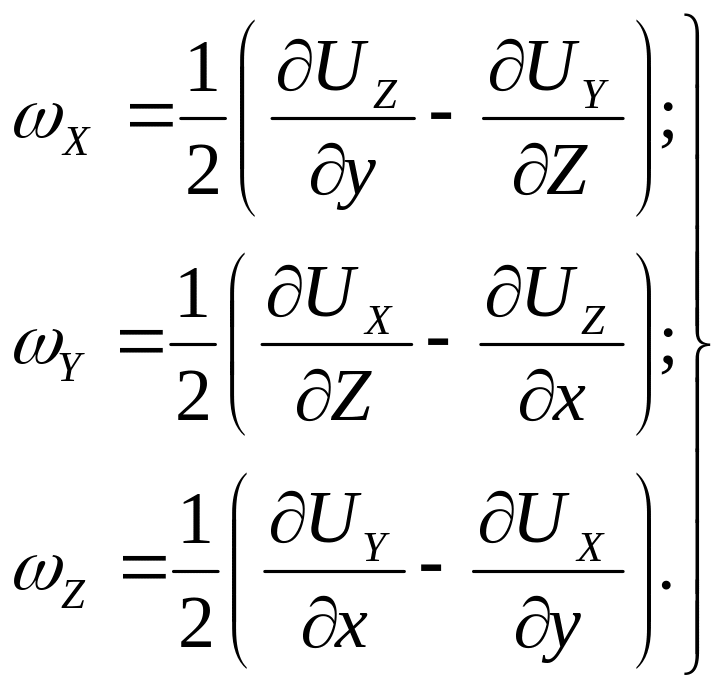(3.24)

Величина вихря, т.е. угловая скорость вращения вокруг мгновенной оси,

Рассмотрим движение при =0 с учетом, что при этом каждый компонент вихря порознь равняется нулю, т.е. _x= _y= _z=0.Такое движение называется безвихревым.

Тогда из (3.24) получается

(3.25)

Безвихревое движение называют потенциальным (или движение с потенциалом скорости) потому, что при наличие равенства (3.25) существует такая функция , частные производные которой по координатам определяют собой величину проекций скорости. Таким образом,

(3.26)

При безвихревом движении функция действительно существует.

В самом деле, пусть имеем некоторую функцию Ее полный дифференциал будет равен

Если существуют равенства (3.26), тогда

то для полного дифференциала функции получим

(3.27)

причем, правая часть уравнения (3.26) должна быть так же полным дифференциалом, а это требует соблюдения равенств (3.25).

Таким образом, если существуют равенства (3.25), то правая часть (3.26) есть полный дифференциал, следовательно, существует функция .

Но эти равенства существуют только при безвихревом движении, следовательно, в этом случае действительно существует и функция , для которой

Если для некоторого конкретного случая будет найдена функция , то дальнейшее исследование данного движения уже не встречает затруднений, так как в этом случае путем прямого дифференцирования найденной функции можно получить основные уравнения в координатах Эйлера, а именно:

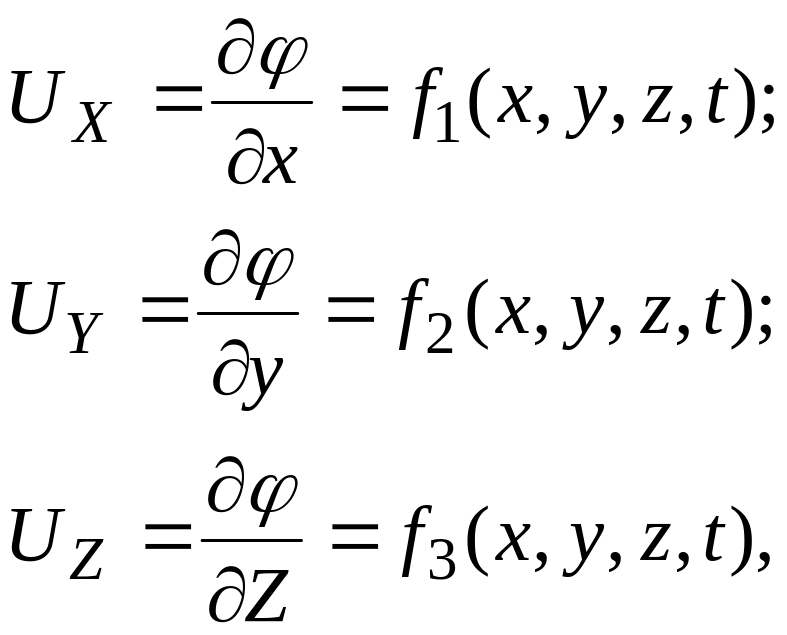
после чего определяются и все иные параметры движения.

Непосредственной подстановкой можно убедиться, что при существовании потенциала скорости уравнение неразрывности (уравнение 3.15) принимает вид

а для случая несжимаемой жидкости (см. уравнение 3.17) оно превращается в уравнение Лапласа:

Потенциал скорости , удовлетворяющий этому уравнению, является гармонической функцией.

При изучении потенциальных потоков большое значение имеют эквипотенциальные поверхности, на которых =const.