3.4. Понятия расхода, средней скорости, живого сечения,

смоченного периметра и гидравлического радиуса

Объем жидкости, протекающей через сечение за единицу времени, называют объемным расходом элементарной струйки dQ:

. (3.11)

Расход потока жидкости равен алгебраической сумме расходов элементарных струек, составляющих данный поток:

. (3.12)

Скорость жидкости U в различных точках поперечного сечения потока, очевидно, может быть неодинаковой, поэтому для характеристики движения всего потока вводится понятие средней скорости потока по сечению (средняя скорость в сечении представляет собой одинаковую для всех точек сечения скорость, при которой проходит тот же расход, какой фактически имеет место при действительных скоростях).

Учитывая, что U = V, получим , или

,

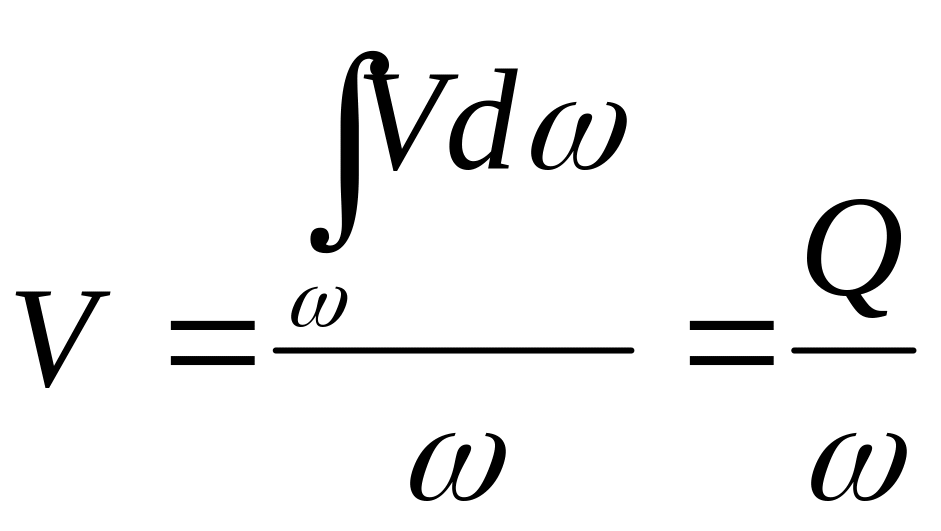из которого следует, что расход потока жидкости равен средней скорости, умноженной на площадь его поперечного сечения:

Q = V. (3.13)

Живым сечением называют сечение потока с поверхностью, нормальной в каждой своей точке к направлению скорости в этой точке.

Поверхность живого сечения может быть плоской или криволинейной. Величина живого сечения определяется его площадью.

Смоченным периметром называют ту часть полного периметра сечения, по которой жидкость соприкасается с твердыми стенками.

Смоченный периметр обозначают обычно греческой буквой .

Гидравлическим радиусом называют отношение живого сечения к смоченному периметру, то есть величину

. (3.14)

Величина R приближенно характеризует форму и размеры живого сечения.

3.5. Уравнение неразрывности

Внутри движущейся жидкости построим параллелепипед АВСДА₁В₁С₁Д₁ (рис. 4), рассматривая его как некоторое неподвиж­ное относительно координатных осей пространство, через которое протекает жидкость.

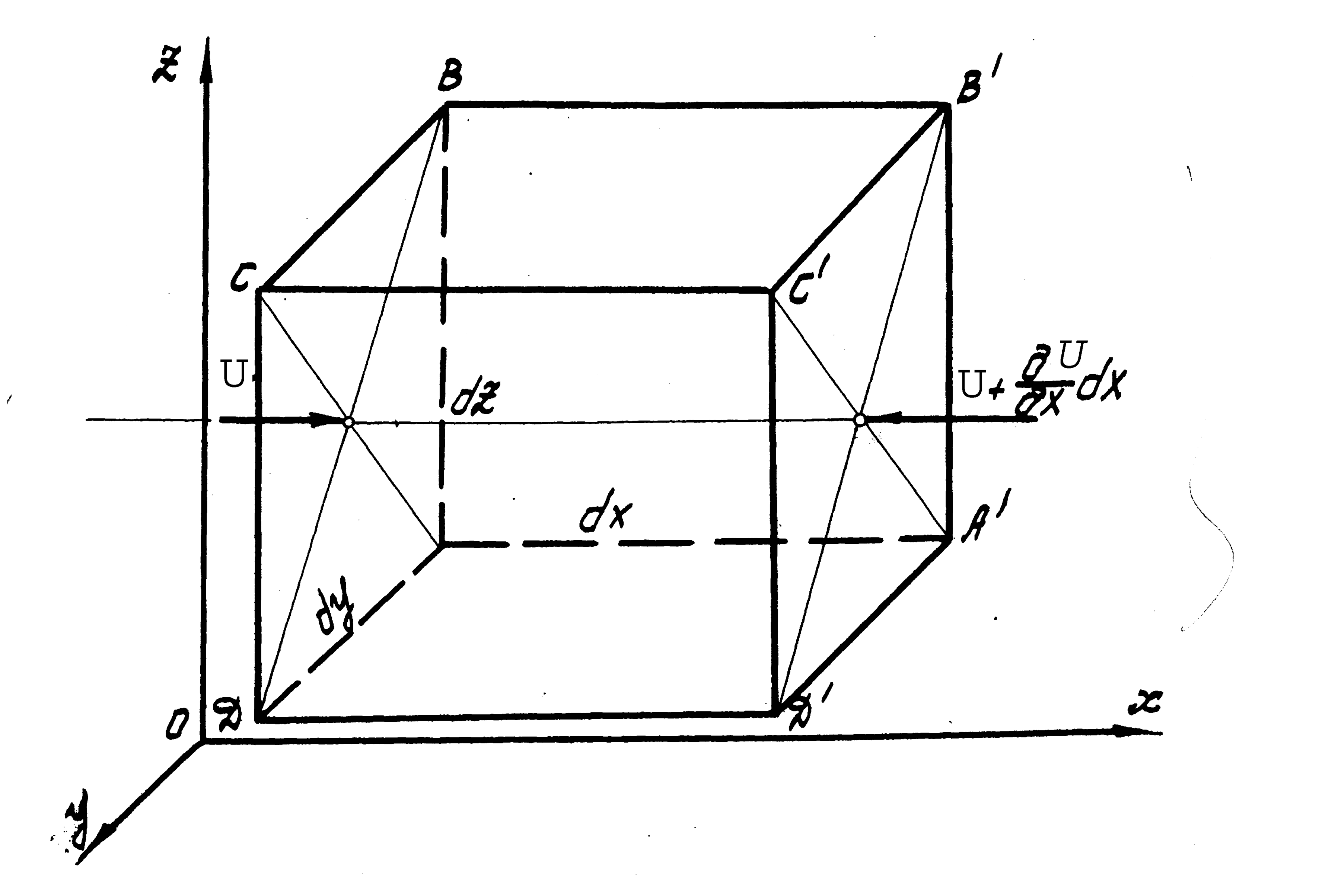
Рис. 4

За время dt через грань АВСДА во внутрь параллелепипеда втекает масса жидкости dM_x , равная

,

а вытекает через грань А₁В₁С₁Д₁ А₁ масса .

Здесь плотность и скорость U на входе в общем случае не равны плотности ₁ и скорости U₁ на выходе. При этом изменение и U обусловливается изменением только координаты x, так как втекание и вытекание происходит одновременно. Поэтому

; .

следовательно,

.

Но

,

а − есть бесконечно малая величина высшего порядка малости относительно других слагаемых и ею можно пренебречь.

Поэтому

.

Если масса жидкости за время dt внутри параллелепипеда уве­личилась за счет притока на величину dM_X, а уменьшилась за счет вытекания на величину dM_1X, то изменение массы вследствие движения вдоль координатной оси ОХ будет равно:

Аналогично найдем, что в итоге движения жидкости вдоль осей ОХ и ОZ изменение массы за время dt соответственно будет равным:

;

.

Следовательно, общее изменение массы за время dt определяется по формуле:

.

Это изменение массы при условии неразрывности движения должно равняться изменению массы, обусловленному изменением плотности. В начальный момент времени t_H масса внутри параллелепипеда

dM_H = dxdydz.

В конечный момент (t+dt) плотность изменяется. Это изменение происходит независимо от координат, поэтому

.

Следовательно, в конечный момент времени t_k=t+dt масса жидкости в объеме параллелепипеда

.

Таким образом, приращение массы за время dt находиться по формуле:

.

При условии неразрывности , т.е.

или после сокращения на dxdydzdt

(3.15)

Это и будет искомое уравнение неразрывности. В частном случае –при установившемся движении −плотность от времени не зависит и .

Поэтому уравнение неразрывности примет вид

(3.16)

И, наконец, для несжимаемой жидкости ( =const) уравнение неразрывности примет вид:

(3.17)

Посмотрим, каким образом можно интерпретировать принцип сплошности движения применительно к струйке жидкости (см. 3.3 рис.3). Выделим в струйке двумя бесконечно близкими сечениями и , находящимися на расстоянии dS друг от друга, объем

.

Масса жидкости, вошедшая в рассматриваемый объем через сечение , в течение некоторого элементарного промежутка времени dt при расходе в струйке dQ будет равна dQdt, масса же, вышедшая через противоположное сечение , будет равна

.

Разность между поступающей и вышедшей массой должна, очевидно, равняться изменению за тот же промежуток времени массы d dS, первоначально заключавшейся в выделенном объеме, т.е. должна равняться

.

Следовательно, имеем равенство

,

откуда

,

или

. (3.18)

В случае мало сжимаемой жидкости изменением плотности вдоль пути dS можно пренебречь и придать уравнению неразрыв­ности более простое выражение:

. (3.19)

Для несжимаемой жидкости ( =const) уравнение неразрывности принимает вид

. (3.20)

В случае

, (3.21)

откуда dQ =const или, так как dQ=U ,

U = const. (3.22)

Таким образом, объемный расход жидкости остается неизменным на всем протяжении данной элементарной струйки.

Так как расход потока жидкости равен алгебраической сумме расходов элементарных струек, условие сплошности потока для несжи­маемой жидкости можно записать в виде

. (3.23)