139

Глава первая

1.1. Системы измерения физических величин,

применяемые в гидравлике

Так как гидравлика изучает законы равновесия и движения жидкостей, логично прежде всего рассмотреть некоторые физические свойства реальных жидкостей. Прежде чем перейти к изучению основных свойств жидкостей, остановимся на единицах измерения, принятых в гидравлике.

За основу принята Международная система единиц измерения (СИ). Кроме того, применяются внесистемные единицы. В инженерной практике используются такие системы МКГСС и СГС.

Основными единицами системы СИ являются:

единица длины – метр (м);

единица массы – килограмм (кг);

единица времени – секунда (с);

единица температуры – градус Кельвина ( К);

единицей силы является Ньютон (Н), т.е. сила, сообщающая массе в 1 кг ускорение в 1 м/с².

Однако до сих пор в инженерной практике измеряют: давление (напор) в технических атмосферах (атм), метрах водяного столба и миллиметрах ртутного столба (м вод. ст. и мм рт. ст.), температуру в градусах Цельсия(⁰С), динамическую вязкость в пуазах(Пз) и кинематическую в стоксах (Ст), работу и энергию в киловаттчасах (кВт·ч).

Чтобы оценивать основные физические свойства жидкостей в различных системах единиц измерения, нужно знать соотношения между ними для этих свойств.

В системе СГС за единицу длины принят – см, за единицу времени – с, за единицу массы – г (масса 1 см³ воды при 4⁰С).

Единицей силы в системе СГС служит длина, т.е. сила, которая массе в 1г сообщает ускорение, равное 1 см/с².

Основные единицы в системе МКГСС:

единица длины – м, единица времени – с, единица силы – килограмм − сила (вес 1 дм³ дистиллированной воды при 4⁰С).

За единицу массы здесь принимается масса, которая под действием силы в 1 кгс получает ускорение, равное 1м/с². Эту единицу часто называют технической единицей массы (тем).

Назовем некоторые основные соотношения, которые служат для пересчета данных из одной системы единиц в другую

Если принять массу m=1, ускорение a = 961 см/с² (ускорение силы тяжести), то получим силу:

в системе СГС (физической)

Р_сгс = 1г · 981 см/с² = 981 дина;

в системе СИ (международной)

Р_СИ = 0,001 кг · 9,81 м/с² = 0,00981 Н;

в системе МКГСС (технической)

Р_МКГСС = 0,001 кгс.

Отсюда имеем

1Н = 100 000 дин = 0,102 кгс;

1 дина = кгс;

1 кгс = 9,81 Н = 981 000 дин.

Поступая подобным образом, можно найти также соотношение между единицами измерения массы в различных системах:

1 кг = 1000 г = 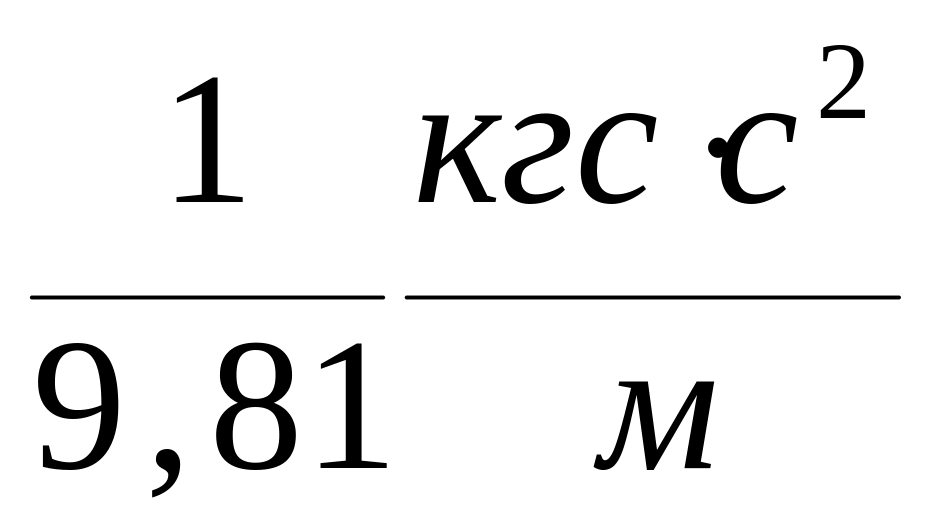(тем).

Размерности и единицы измерения других физических единиц, с которыми приходится иметь дело при гидравлических расчетах, легко получить как производные от установленных выше основных единиц измерения.

1.2. Основные физические свойства жидкостей

Плотность жидкостей

Плотностью жидкости называется ее масса, заключенная в единице объема:

, , (1.1)

где М – масса жидкости; W – объем этой жидкости.

Плотность воды при 4⁰С:

_{в 4}⁰С = 1000 = 102 .

В практических приложениях о массе жидкости судят по ее весу.

Вес жидкости, приходящийся на единицу объема, называется удельным весом:

,

где G – вес жидкости; W – объем этой жидкости.

Удельный вес воды при 4⁰С

. (1.2)

Поскольку

G = M · g , (1.3)

· g , (1.4)

где g – ускорение свободного падения.

Относительным удельным весом жидкости (или относительным весом) называется отношение удельного веса данной жидкости к удельному весу дистиллированной воды при 4⁰С:

. (1.5)

Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия , который представляет собой относительное уменьшение объема жидкости на единицу увеличения напряжения сжатия:

, (1.6)

где W –первоначальный объем жидкости; –уменьшение этого объема при увеличении сжимающего напряжения на величину .

Коэффициент объемного сжатия в системе СИ имеет размерность .

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости:

, . (1.7)

Как показывают исследования, при повышении сжимающего напряжения на 9,81 * 10⁴ Па (1 ат) объем воды уменьшается в среднем на 1/20000 часть первоначальной величины.

Для воды

или ,

Е_В = 2 · 10⁹ П_а.

Вязкость жидкостей

Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц или слоев жидкости. Таким образом, вязкость характеризует степень текучести жидкости или подвижности ее частиц.

Впервые наличие внутреннего трения в жидкостях было отмечено И. Ньютоном, высказавшем в 1687 г. гипотезу о том, что величина силы внутреннего трения между смежными слоями жидкости зависит от свойств жидкости, пропорциональна площади поверхности соприкасаемых слоев (площади трения) и их относительной скорости перемещения.

Справедливость гипотезы И. Ньютона была доказана русским ученым и инженером Н.П. Петровым в его работе «Трение в машинах и влияние на него смазывающей жидкости», вышедшей в 1883 году. В результате исследования движения жидкости при небольших скоростях в прямолинейной трубе круглого сечения была предложена зависимость

, (1.8)

или

, (1.9)

где Т – сила внутреннего трения; –динамический коэффициент вязкости, т.е. коэффициент, характеризующий сопротивляемость данной жидкости сдвигу. Величина, аналогичная коэффициенту сдвига в твердых телах; F – площадь поверхности соприкасающихся слоев; –градиент скорости (относительный сдвиг); −абсолютный сдвиг (скорость смещения одного слоя относительно другого); –расстояние между осями двух смежных слоев; –напряжение сил внутреннего трения, возникающих по поверхности соприкосновения слоев.

Знак «+» или «-» принимают в зависимости от знака градиента скорости , чтобы всегда было положительным.

Соотношение 1.8 так же, как и 1.9, называется законом продольного внутреннего трения в жидкостях Ньютона. Поясним этот закон рисунком.

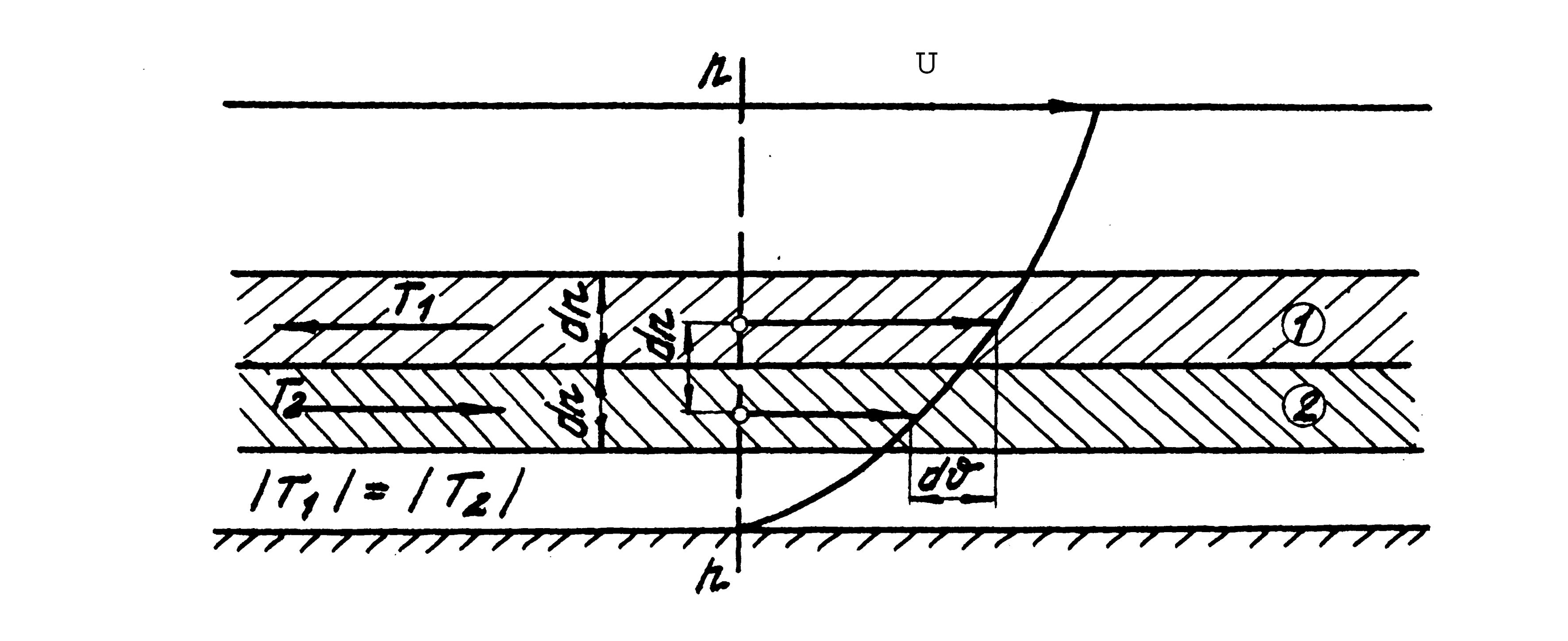
Как видите, трение в жидкости отличается от трения в твердых телах, где сила трения зависит от нормального давления и не зависит от площади трущихся поверхностей и скорости:

.

В системе СИ выражается в или Па·с.

В системе МКГСС динамический коэффициент вязкости имеет размерность .

В системе СГС за единицу динамической вязкости принят пуаз (Пз) в честь французского врача Пуазеля, исследовавшего законы движения крови в сосудах человеческого тела, .

Соотношение между _СИ и _СГС следующее:

,

.

1Пз = 1 г/см·с = 0,001 кг/0,01 м·с = 0,1 кг/м·с = 0,1 Па · с,

т.е. 1Пз = 0,1 Па·с, 1Пз = 1 дина·с/см² = 10^-5 Н с/10^-4м² = 0,1Н·с/м² = =0,1 Па·с.

Для пресной воды при t = 10⁰С

Па·с.

В расчетах часто применяют кинематический коэффициент вязкости .

Связь между и выражается зависимостью:

, (1.10)

где –плотность жидкости.

Размерность в системе МКГСС – м²/с, в системе СГС – см²/с, в системе СИ –м²/с.

1см²/с = 1 стокс (ст). Для воды при t = 10⁰С

= 0,0131 см²/с = 0,0131 ст = 1,31 сст.

Глава вторая

ГИДРОСТАТИКА