
- •Общие понятия Теории дискретных линейных систем
- •Линейные системы с постоянными параметрами
- •Физическая реализуемость линейной системы
- •Классические методы анализа временных рядов
- •Некоторые понятия теории случайных процессов
- •Классификация случайных процессов
- •Вычисление среднего значения и дисперсии
- •Корреляционный анализ
- •Автокорреляционная функция
- •Взаимная корреляционная функция (вкф)
- •Спектральный анализ
- •Преобразование Фурье и его основные свойства
- •Быстрое преобразование Фурье
- •Алгоритмы бпф с основанием 2
- •Функция спектральной плотности
- •Определение спектральной плотности через ковариационную функцию
- •Функция когерентности
- •Основные понятия линейной дискретной системы.
- •Введение в цифровые фильтры. Основные определения и классификация.
- •Синтез цифровых фильтров и задание требований к цифровым фильтрам
- •Типы избирательных фильтров и задание требований к ним
- •Постановка задачи оптимального синтеза
- •Представление сигналов в р – области
- •Синтез бих- фильтров
- •Методы синтеза аналоговых фильтров прототипов
- •Реактансные преобразования
- •Аппроксимация ачх рациональными функциями
- •Фильтр Баттерворта.
- •Фильтр Чебышева
- •Эллиптические фильтры
- •Фильтр Бесселя
- •Синтез бих- фильтров методом стандартного z- преобразования.
- •Процедура синтеза бих-фильтров методом билинейного z- преобразования
- •Основы адаптивной обработки сигналов.
- •Классификация адаптивных систем
- •Постановка задачи адаптивной обработки сигналов
- •Многоскоростные системы цос
- •Однократные системы интерполяции
- •Однократные системы децимации
- •Интерполяционный полином Лагранжа
- •Интерполяционный полином Ньютона
- •Интерполяция сплайнами
- •На основании соотношения
- •Общие понятия
- •Числовые характеристики киг
- •Статистический анализ ср
- •Теоретическое введение
- •Простейшие пороговые методы
- •Метод сравнения с образцом
- •Метод на основе цифровой фильтрации
- •Структурные методы
- •Пример алгоритма, основанного на применении структурного метода
- •Основные понятия
- •Последовательность действий при картировании
- •Теоретическое введение
- •Простейший апертурный метод
- •Алгоритмы интерполяции и экстраполяции
- •Сущность метода синхронного накопления и усреднения
- •Основные ограничения, накладываемые на сигнал вп
- •Недостатки метода усреднения, другие методы выделения вп
Функция когерентности
Функция когерентности определяется следующим образом:
![]()
Функция когерентности является аналогом коэффициента корреляции в частотной области и отражает степень линейной взаимосвязи гармонических компонент рассматриваемых процессов. Чем ближе функция когерентности к 1 на конкретной частоте f, тем больше совпадения гармонических составляющих на этой частоте. Как правило, именно функция когерентности, а не взаимная спектральная плотность используется в практических приложениях для анализа связанности процессов в частотной области.
Лекция 4. Wavelet-анализ.
Вейвлет анализ широко используется для нестационарных случайных процессов. Он показал свою эффективность для решения широкого класса задач, связанных с подавлением шумов, сжатием больших объемов информации.
Вейвлет анализ, как и преобразование Фурье, состоит в вычислении корреляции между анализируемым временным рядом и базисной функцией преобразования. Вейвлет преобразование, состоящее в разложении ряда по базису, сконструированному из обладающих определенными свойствами функций, называется Вейвлетом (маленькая волна) посредством ее масштабных изменений и переносов. Каждая вейвлет функция базиса характеризуется определенным масштабом (частотой) и локализацией во времени. В отличие от преобразования Фурье вейвлет преобразование дает двумерную развертку одномерного процесса, при этом частота и время рассматриваются как независимые переменные. В результате появляется возможность анализировать свойства процесса одновременно в частотной и временной областях. В основе вейвлет преобразования лежит идея многомасштабного анализа, который заключается в последовательном огрублении исходной информации, содержащейся в процессе.
Данный подход
позволяет выявлять локальные области
процесса и классифицировать их по
интенсивности; отслеживать динамику
частотного состава процесса во времени.
Операция огрубления исходной информации
осуществляется путем сглаживания
исходного ряда с помощью функции вейвлета
![]() .
Термин вейвлет обозначает локализованные
во временной и частотной областях
функции, обладающие следующими свойствами:
.
Термин вейвлет обозначает локализованные
во временной и частотной областях
функции, обладающие следующими свойствами:
Вейвлет имеет среднее значение, равное нулю:
![]() .
.
Ограниченность функции вейвлета, т.е. она быстро убывает при
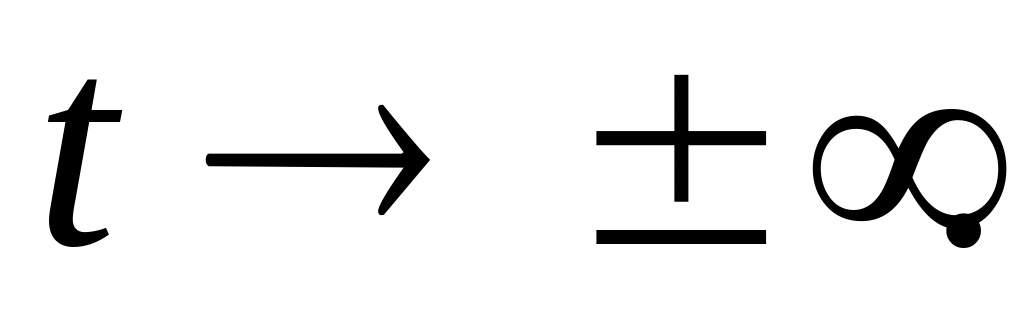
Автомодельность, т.е. при любых масштабных изменениях вейвлета его форма (количество экстремумов) не меняется.
Данные свойства определяют большой класс действительных и комплексных функций, которые являются вейвлетами. Вейвлет локализован сразу в двух областях: временной и частотной. Для осуществления вейвлет преобразования произвольного временного ряда x(t) необходимо предусмотреть возможность сдвигов функции вейвлета вдоль временной оси и масштабных преобразований в частотной области путем сжатия или растяжения исходного вейвлета. Такую возможность реализует базисная функция следующего вида:
![]() .
.
Соответственно, вейвлет преобразование сигнала имеет вид:
![]() (4.1)
(4.1)
В этой формуле a и b являются действительными числами и определяют масштаб (величину обратно пропорциональную частоте) и временной сдвиг соответственно.
На основе этой
базисной функции вейвлет преобразование
временного ряда x(t)
определенного на всей временной оси
(![]() )
записывается в виде (4.1). В формуле (4.1)
параметр «b»
меняется в интервале от
)
записывается в виде (4.1). В формуле (4.1)
параметр «b»
меняется в интервале от
![]() до
до
![]() ,
пробегая всю временную ось, т.е. всю
временную область, на которой определена
функция x(t).
Параметр «a»
меняется от 0 до
.
При использовании действительной
функции вейвлета в результате
преобразования получается двумерный
массив коэффициентов W(a,b),
а при применении комплексной функции
вейвлета в результате получаются
двумерные массивы модуля и фазы:
,
пробегая всю временную ось, т.е. всю
временную область, на которой определена
функция x(t).
Параметр «a»
меняется от 0 до
.
При использовании действительной
функции вейвлета в результате
преобразования получается двумерный
массив коэффициентов W(a,b),
а при применении комплексной функции
вейвлета в результате получаются
двумерные массивы модуля и фазы:

Алгоритм вычисления коэффициента вейвлет преобразования по формуле (4.1) для каждой пары параметров «a» и «b» выглядит следующим образом:
растянуть вейвлет
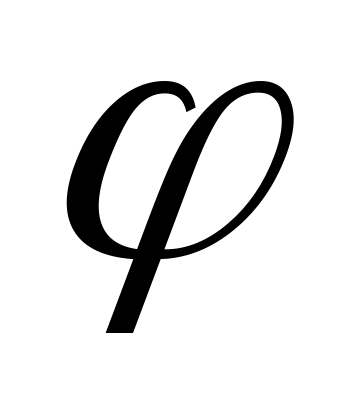 в a
раз по горизонтали в 1/a
раз по вертикали;
в a
раз по горизонтали в 1/a
раз по вертикали;сдвинуть вейвлет в точку
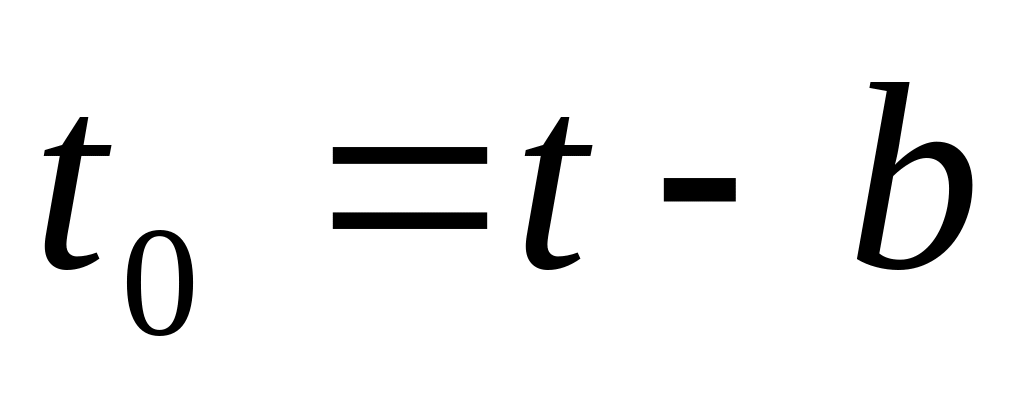 по оси времени;
по оси времени;произвести вычисление вейвлета по (4.1) и усреднить значение полученной функции по ширине окна самого вейвлета;
Далее процедура повторяется для другой пары параметров «a» и «b» до тех пор, пока не будут рассчитаны вейвлет преобразования для всех значений «a» и «b». Полученные результаты Wab представляются на графике преобразования следующим образом:
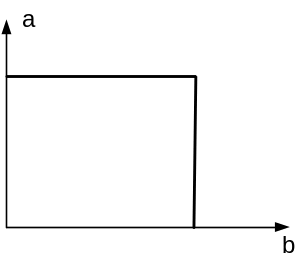
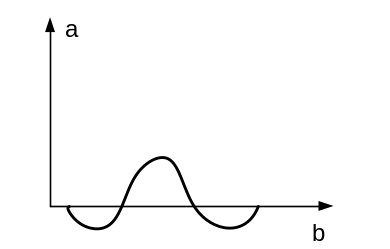
Результат кодируется цветом. Два наиболее распространенных вейвлета, применяемых в медицинских целях называются Сомбреро и Вейвлет Морле.
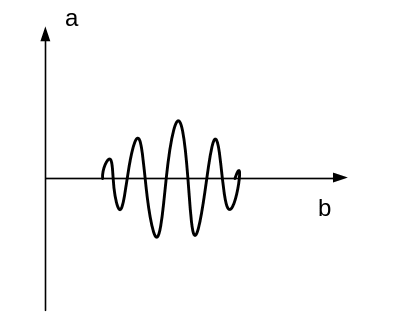 Вейвлет
Морле
Вейвлет
Морле
Сомбреро
Для дискретных сигналов формула расчета вейвлет-преобразования имеет вид:
![]() (4.2)
(4.2)
сигнал, представленный в виде дискретных цифровых отсчетов;
![]() вейвлет;
вейвлет;
![]() длительность
окна вейвлет преобразования.
длительность
окна вейвлет преобразования.
В медицинских целях вейвлет преобразование может применяться для сжатия исходных сигналов. В этом случае необходимо знать формулу обратного вейвлет преобразования, позволяющего восстановить исходный временной ряд:
![]()
![]() нормализующий
коэффициент.
нормализующий
коэффициент.
Лекция 5. Основные характеристики линейных дискретных систем. Введение в цифровые фильтры. Основные определения и классификация цифровых фильтров.
