Взаимная корреляционная функция (вкф)

ВКФ рассматривает два разных процесса или сигнала и определяет степень связности этих процессов между собой:

(2.4)

Для дискретного представления сигнала:

где , (2.5)

Т – интервал времени, используемый для анализа.

Возможные виды ВКФ:

Т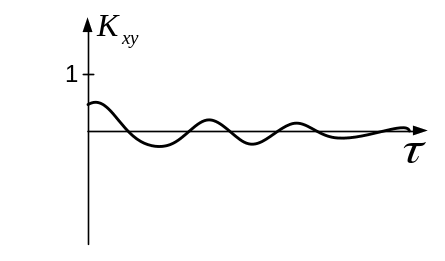 акая ВКФ показывает, что два процесса слабо связаны между собой и не имеют гармонических составляющих.

Э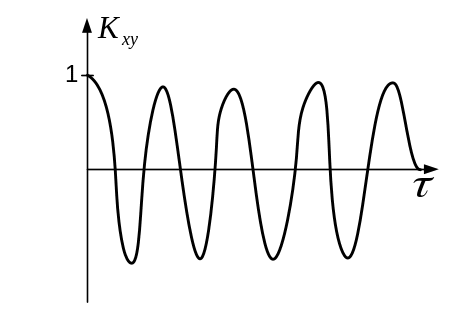 та ВКФ показывает, что процессы сильно связаны между собой и имеют общие гармонические компоненты.

Т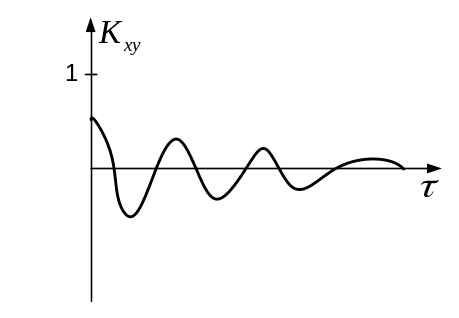 акая ВКФ показывает, что процессы имеют незначительные общие гармонические составляющие и несильно связаны.

Т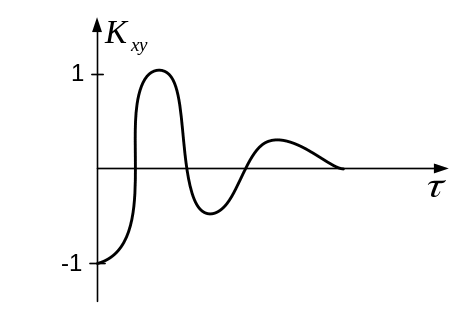 акой вид ВКФ показывает, что процессы имеют общие гармонические составляющие, но сдвинуты по фазе между собой.

Рассмотрим математические характеристики ВКФ:

1. коэффициент кросскорреляции – это значение ВКФ при :

Если коэффициент кросскорреляции близок к единице (0,9<К_кр<1), то степень корреляционной связи двух процессов считается очень высокой. Если коэффициент кросскорреляции находится в пределе 0,7<К_кр<0, то связь считается высокой. Если 0,5<К_кр<0,7, то связь значительная. Если 0,3<К_кр<0,5, то умеренная. Если К_кр<0,3, то слабая. Если получаются те же значения со знаком « - », то добавляется, что процессы находятся в противофазе.

2. степень кросскорреляционной связи – это отношение максимального значения ВКФ к величине максимума АКФ каждого из исследуемых процессов. Так как максимумы АКФ приводят к единице, то степень кросскорреляционной связи К_с фактически равна максимальному значению ВКФ, взятому по модулю.

3. временной сдвиг определяется как интервал времени до максимального значения ВКФ.

Спектральный анализ

С помощью спектрального анализа можно характеризовать частотный состав исследуемого временного ряда. Математической основой, которая связывает временной сигнал с его представлением в частотной области, является преобразование Фурье. Это преобразование играет важную роль не только как инструмент получения спектрального состава сигнала, но также как необходимый промежуточный этап при вычислении некоторых характеристик.

Преобразование Фурье и его основные свойства

Общий вид преобразования Фурье для непрерывных сигналов:

, где (2.6)

временной ряд (исследуемый сигнал),

j- мнимая единица,

f- частота,

t- интервал времени, на котором производится анализ.

Преобразование Фурье существует, если выполняется условие абсолютной интегрируемости функции x(t), т.е.:

<

Обратное преобразование Фурье – переход от частотной области к временной:

Непрерывно – дискретное преобразование Фурье применяется для дискретных сигналов:

где

Т – участки временного ряда, имеющие непрерывную характеристику.

Другая запись:

Дискретное преобразование Фурье используется для анализа дискретных сигналов, каковыми в большинстве своем являются медицинские сигналы. Формула для него имеет следующий вид:

(2.7)

Обратное преобразование имеет следующий вид:

, где

временной ряд, представленный в виде дискретных отсчетов;

представленный в виде дискретных значений частотный ряд, отражающий спектральную оценку сигналов;

интервал времени, выраженный в количестве дискретных отсчетов, которые используются для анализа;

дискретно представленный частотный диапазон, в котором производится частотное представление сигналов.

Формула перехода от логарифмического состава к тригонометрическому:

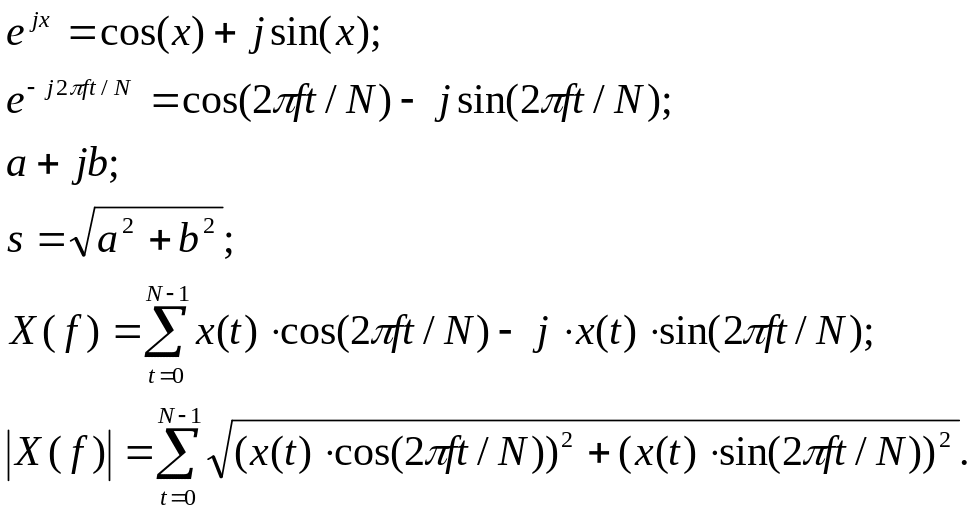
Лекция 3. Алгоритмы быстрого и дискретного преобразования Фурье. Функция спектральной плотности мощности. Алгоритмы ее определения. Функции когерентности и алгоритмы ее определения.