Многоскоростные системы цос
В некоторых системах ЦОС необходимым либо эффективным является реализация различных этапов обработки данных на разных частотах дискретизации. Такие системы являются системами с многочастотными дискретизациями, более известными как многоскоростные ЦОС.
В таких системах для сопряжения различных этапов обработки данных необходимо решать задачу преобразования частоты дискретизации:
1. от меньшей к большей, то есть повышение этой частоты в целое число раз, называемое интерполяцией;
2. от большей к меньшей, то есть понижение частоты в целое число раз, называемое децимацией.
Для систем
интерполяции:
;
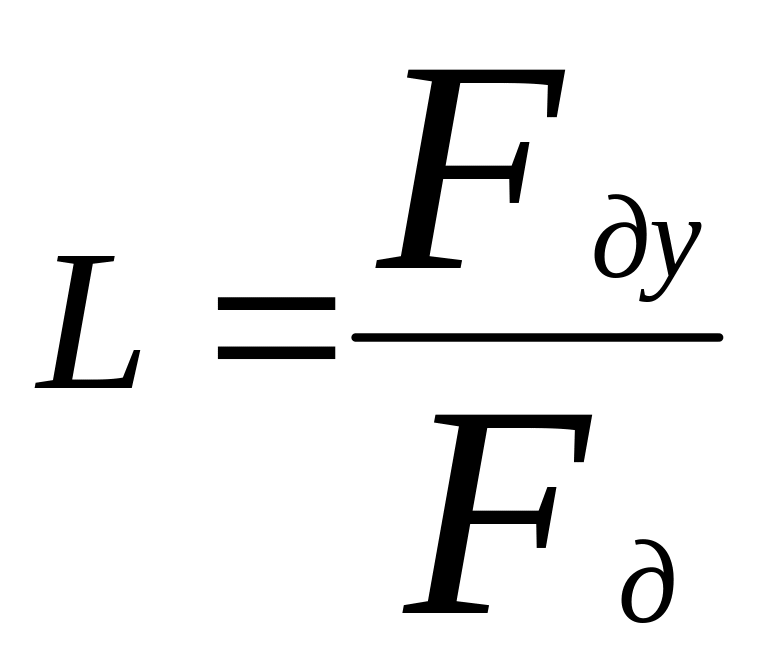для систем децимации:
.
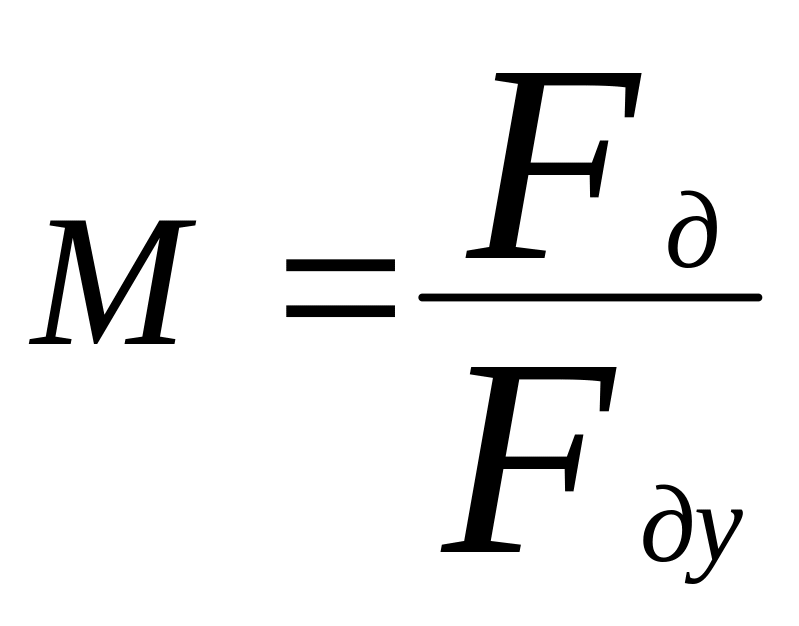Эти коэффициенты обязательно должны
быть целыми.
Fду – частота дискретизации на выходе системы; Fд – частота дискретизации на входе.
Многоскоростные системы, в которых уменьшение или увеличение частоты дискретизации реализуется в один прием, называются однократными. Многократными называются системы, образованные последовательным соединением однократных систем.
Помимо систем интерполяции и децимации с целочисленными коэффициентами L и M существуют также системы преобразования частоты с дробными коэффициентами, равными L/M. Они строятся по принципу последовательного вычисления интерполяций и децимаций.
В теории ЦОС смысл термина интерполяция не тождественен общепринятому математическому; равно как и смысл термина децимации не заключается в отбрасывании некоторого количества отсчетов между каждой парой сохраняемых отсчетов на периоде.
Преобразование частоты определяется как ЦОС с помощью операции линейной фильтрации, в результате которой формируется выходной сигнал с новой частотой дискретизации. При этом на временные и спектральные изменения выходного сигнала накладываются определенные ограничения.
Однократные системы интерполяции
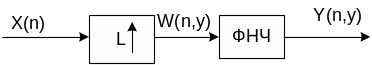
Процедура интерполяции выполняется в 2 этапа: на 1 этапе из входного сигнала формируется промежуточный сигнал w(n,y) с частотой дискретизации fду и интервалом дискретизации Ту=Т/L; на 2 этапе из промежуточного сигнала w(n,y) формируется искомый выходной сигнал Y(n,y) той же частоты в результате операции линейной цифровой фильтрации.
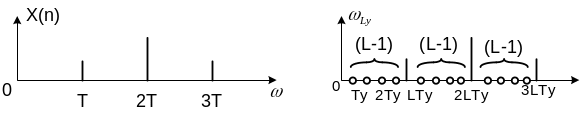
Процедура повышения частоты дискретизации называется экспандером. Сигнал на выходе экспандера заполняется (L-1) нулевыми отсчетами между каждой парой отсчетов входного сигнала на его периоде дискретизации.
в
L раз (9.1)
Для сигнала w(n,y) верхняя полоса пропускания Fву получается из соотношения согласно теореме Найквиста (9.1). Соответственно верхняя полоса пропускания сигнала w(n,y) будет превышать верхнюю полосу пропускания сигнала X(n), что искажает спектр сигнала, а соответственно влияет на его частотные свойства. Для устранения данных искажений на втором этапе применяется ФНЧ с частотой среза, равной Fв исходного сигнала.
Однократные системы децимации
Процедура децимации так же выполняется в 2 этапа и обозначается диаграммой:
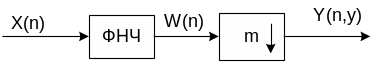
На первом этапе формируется промежуточный сигнал w(n) из входного сигнала X(n) в результате операции линейной фильтрации; на втором этапе из промежуточного сигнала формируется искомый сигнал Y(n,y) с интервалом Ту=mТ.
Согласно теореме Найквиста при понижении частоты дискретизации в m раз при неизменной верхней полосе пропускания произойдет эффект наложения спектров, который повлечет за собой частотные изменения сигнала. Чтобы этого избежать верхнюю полосу спектра входного сигнала равную Fв=Fд/2 нужно уменьшить в m раз согласно формуле Fву=Fд/(2m). Эта процедура выполняется с помощью линейного ФНЧ.
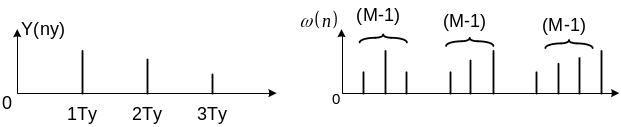
Из промежуточного сигнала w(n) формируется выходной сигнал Y(n,y) путем прореживания отсчетов промежуточного сигнала, то есть из последовательности отсчетов w(n) берется каждый m-ый отсчет.
Процедура понижения частоты дискретизации называется компрессором.
Лекция 10. Методы аппроксимации функций.
При анализе биомедицинских сигналов важно иметь возможность получения аналитического выражения, описывающего сигнал, представленный последовательностью отсчетов. Для этих целей используется такой математический аппарат, как интерполяция. Далее будут рассмотрены основные виды интерполяции, применяемые в медицинских системах.
Задачей интерполяции в узком смысле считают нахождение приближенных значений табличной функции при аргументах х, не совпадающих с узловыми. Если значение аргумента х расположено между узлами x0 и xn, то нахождение приближенного значения функции f(x) называют интерполяцией, если аппроксимирующую функцию вычисляют вне этого интервала, то процесс называют экстраполяцией. Происхождение этих терминов связано с латинскими словами inter - между, внутри, ро1е - узел, extra - вне.
Интерполяция каноническим полиномом
Пусть функция f(x) задана таблицей значений, представляющей последовательность отсчетов некоего биомедицинского сигнала.
Введем аппроксимирующую функцию (x, c0, c1,…, cn) так, чтобы она совпадала с табличными значениями во всех узлах xi:
(x, c0, c1,...,cn)=fi , 0 i n. (10.1)
Свободные параметры сi определяются из системы (10.1).
Подобный способ введения аппроксимирующей функции называется лагранжевой интерполяцией, а соотношения (10.1) - условиями Лагранжа.
Выберем в качестве аппроксимирующей функции (х) полином Рn (х) степени n в каноническом виде
(х) =Pn(x)=c0+c1x+c2x2+...+cnxn . (10.2)
Свободными параметрами интерполяции сi являются коэффициенты полинома (10.2). Интерполяция полиномами обладает такими преимуществами, как простота вычислений их значений, дифференцирования и интегрирования. Коэффициенты сi определим из условий Лагранжа
Рп(хi) = fi, 0 i п
или
c0 + c1x0+c2x02+…+cnxn0 = f0,
c0 + c1x1+c2x12 +…+cnxn1 = f1,
c0 + c1xn + c2xn2 + …+cnxnn = fn.
Эта система линейных алгебраических уравнений относительно свободных параметров сi имеет решение, так как определитель системы отличен от нуля, если среди узлов xi нет совпадающих. Определитель системы называется определителем Вандермонда и имеет аналитическое выражение.