Фильтр Чебышева
Чтобы получить достаточно крутую характеристику АЧХ в переходной области для фильтра Баттерворта необходимо использовать очень высокий порядок. Ту же характеристику в переходной полосе и при гораздо меньшем порядке, можно получить с помощью фильтров Чебышева, в которых ошибка аппроксимации равномерно распределена по полосе пропускания или по полосе задерживания. В зависимости от области, в которой минимизируется ошибка аппроксимации, различают фильтры Чебышева I и II рода.
Фильтр I рода в полосе пропускания имеет равноволновой характер аппроксимации АЧХ, а в полосе задерживания – оптимально плоский. Фильтр II рода в полосе задерживания имеет волновой характер аппроксимации, а в полосе пропускания – оптимально плоский.
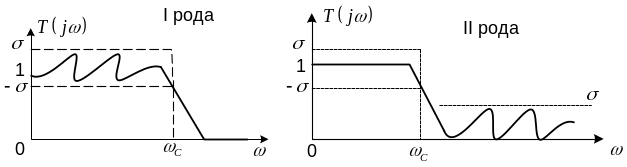
АЧХ фильтра Чебышева I рода:
,
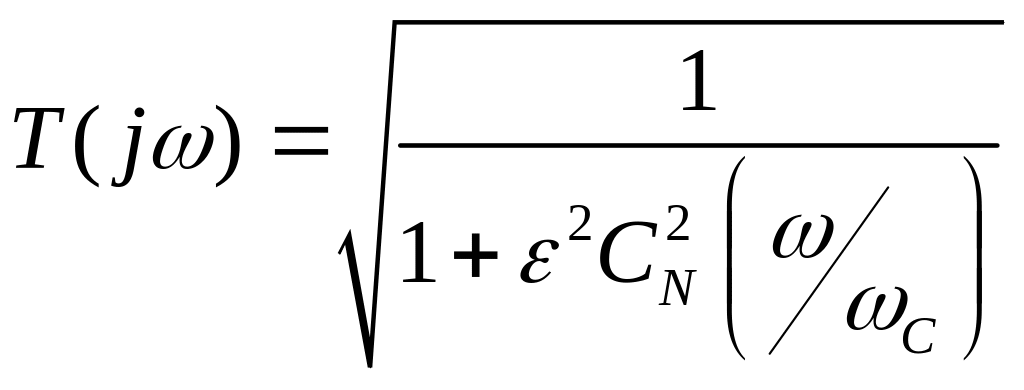где
;
Нули у фильтра Чебышева I рода не вычисляются, а для полюсов используется следующая формула:
Для фильтров Чебышева II рода используется следующий вид аппроксимирующего АЧХ полинома:
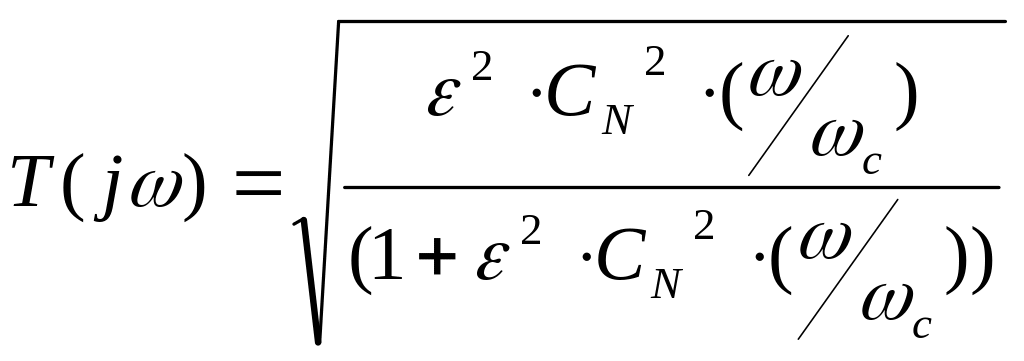
Полюса рассчитываются по формуле:
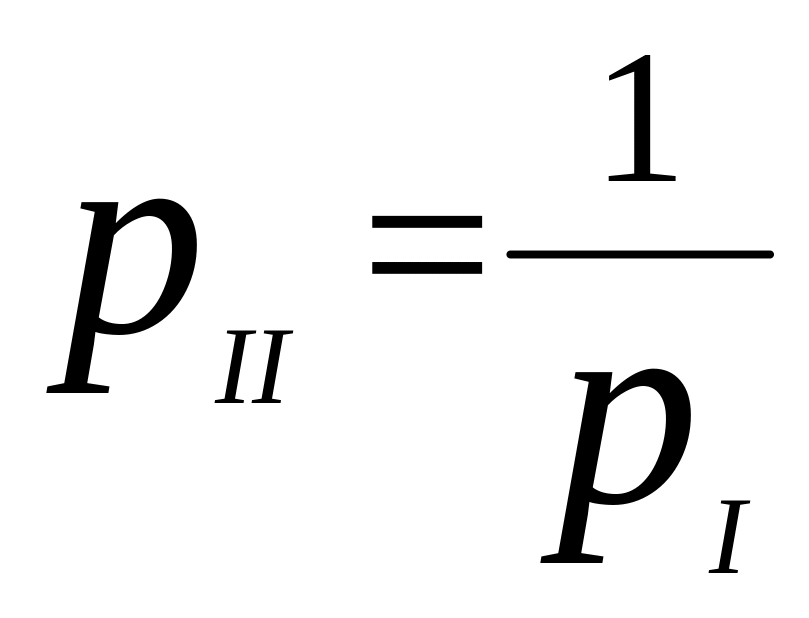
Нули рассчитываются по формуле:
Эллиптические фильтры
Они характеризуются равноволновой АЧХ как в полосе пропускания, так и в полосе задерживания; но более крутой характеристикой в переходной полосе при тех же порядках, что и в фильтре Чебышева.
Поэтому такие фильтры применяют в задачах, требующих высокой избирательности и не критичных к виду фазочастотной характеристики, которая не является линейной.
,
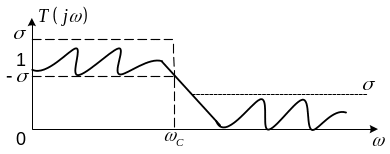
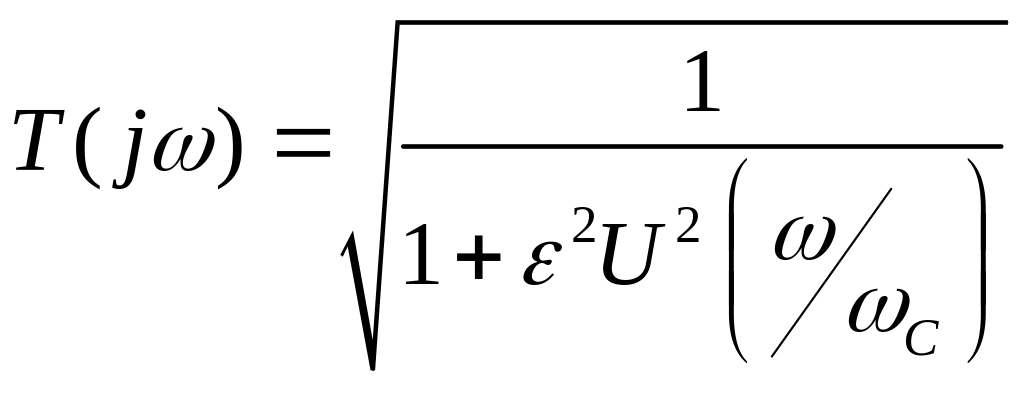где
-
эллиптический полином
Данный тип фильтра не так часто используется в связи со сложностью его расчета.
Фильтр Бесселя
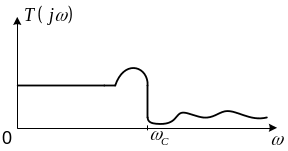
Для него аналитическая АЧХ не задается, а задается передаточная функция:
,
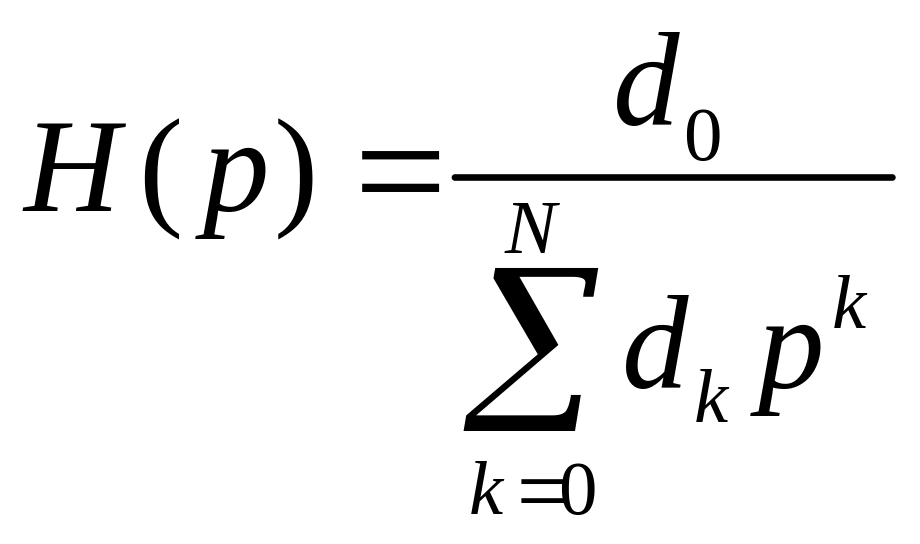где
Синтез бих- фильтров методом стандартного z- преобразования.
Данный метод использует прямую дискретизацию аналоговых БИХ- фильтров. Иначе он называется методом инвариантности импульсной характеристики аналогового фильтра-прототипа. Под инвариантностью понимают равенство цифровых отсчетов импульсной характеристики цифрового фильтра h(nT) и значений импульсной характеристики аналогового фильтра-прототипа g(t).
Для решения задачи синтеза таким методом необходимо:
1. найти импульсную характеристику прототипа g(t);
2. получить импульсную характеристику БИХ-фильтра h(nT) путем дискретизации g(t) с шагом дискретизации T;
3. найти передаточную функцию БИХ-фильтра, выполнив следующее преобразование от полученной импульсной характеристики h(nT):
Алгоритм синтеза БИХ-фильтров методом стандартного z- преобразования:
1. задать требования к ЦФ (тип частотной избирательности, граничные значения частот, допуски АЧХ в полосах пропускания и задерживания и тип фильтра по виду аппроксимируемого полинома);
2. рассчитать нули и полюсы аналогового фильтра-прототипа с помощью реактансных преобразований;
3. на основании рассчитанных нулей о полюсов построить передаточную функцию АФ G( p);
4. разложить G( p) на простые дроби вида:
;
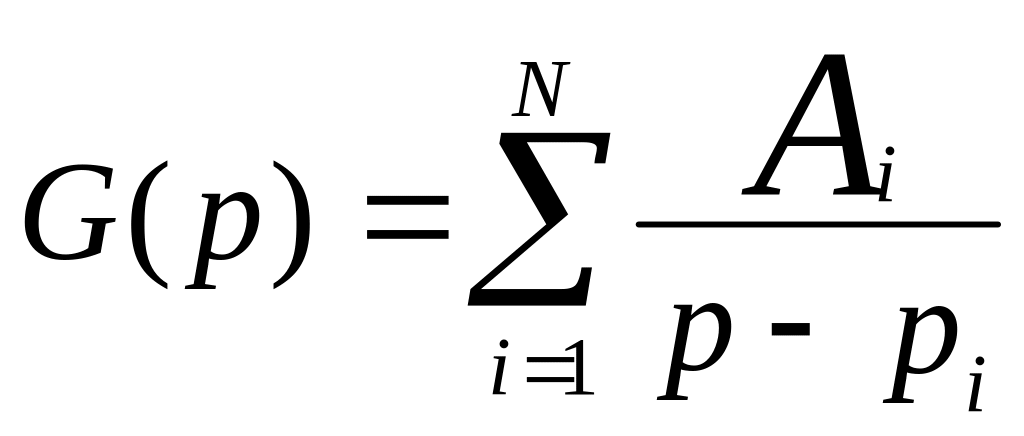5. используя дискретизацию перейти от передаточной функции G(p) к передаточной функции H(z).
Основным недостатком метода инвариантности импульсной характеристики прототипа является искажение АЧХ соответствующего цифрового фильтра вследствие наложения АЧХ, что объясняется периодичностью, а потому и неоднозначностью отображения р-плоскости на z-плоскость. Причем эти искажения оказываются столь велики, что метод инвариантности накладывает ограничения на синтез цифровых фильтров верхних частот, режекторных и широкополосных фильтров.