ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное учреждение

высшего профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Семестровый курс лекций по дисциплине "Методы обработки биомедицинских сигналов и данных"

Работу выполнил

к.т.н., доцент Сахаров В.Л.

(должность, звание, ФИО)

Таганрог

2008

Лекция 1. Основные типы сигналов. Общие понятия теории дискретных линейных систем. Некоторые понятия теории случайных процессов.

ОСНОВНЫЕ ТИПЫ СИГНАЛОВ

К основным типам сигналов относятся аналоговый, дискретный и цифровой. Аналоговым называется сигнал, непрерывный во времени и по состоянию. Это означает, что сигнал описывается непрерывной (или кусочно-непрерывной) функцией x(t), причем и аргумент, и сама функция могут принимать любые значения из некоторых: .

Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию. (рис. 1) Он описывается решетчатой функцией x(nT), где n – номер отсчета, n = 0, 1, 2, 3 … Интервал T называется периодом дискретизации, а обратную величину - частотой дискретизации.

Цифровым называется сигнал, дискретный как во времени, так и по состоянию. Сигналы этого типа также описываются решетчатой функцией x (nT), однако могут принимать только конечное число значений из некоторого конечного интервала . Эти значения называются уровнями квантования, а соответствующие функции – квантованными.

Общие понятия Теории дискретных линейных систем

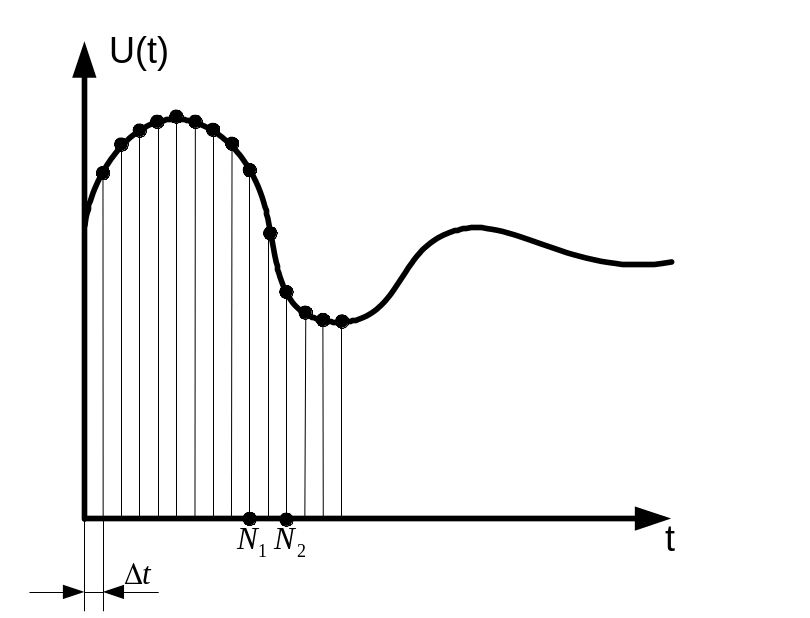
Рис.1

Теория дискретных линейных систем связана с описанием и обработкой временных и частотных последовательностей.

При переходе из аналогового представления в цифровое отмечаются цифровые отсчеты на данном сигнале, которые и будут представлять собой цифровой сигнал. Процедура преобразования аналогового сигнала в цифровой называется дискретизаций. Основными параметрами дискретизации являются:

• интервал между двумя соседними цифровыми отсчетами, называемый интервалом дискретизации;

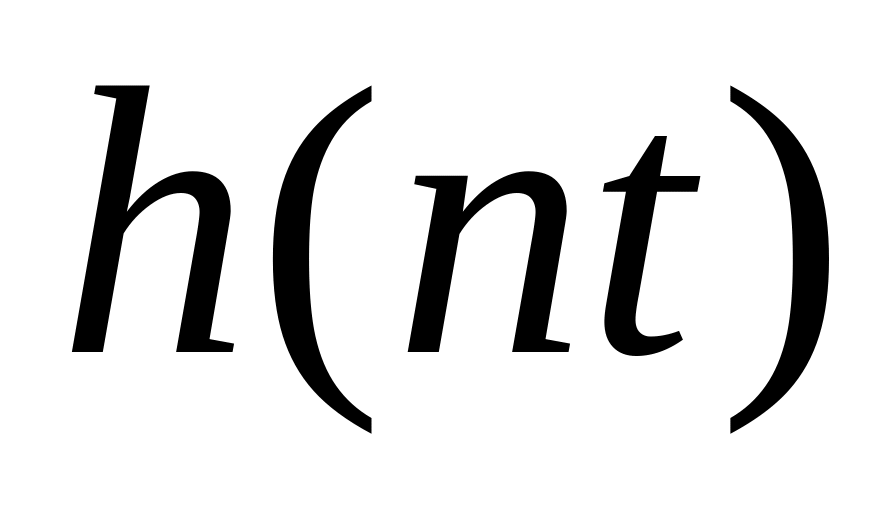
• значение цифрового отсчета, соответствующее его амплиту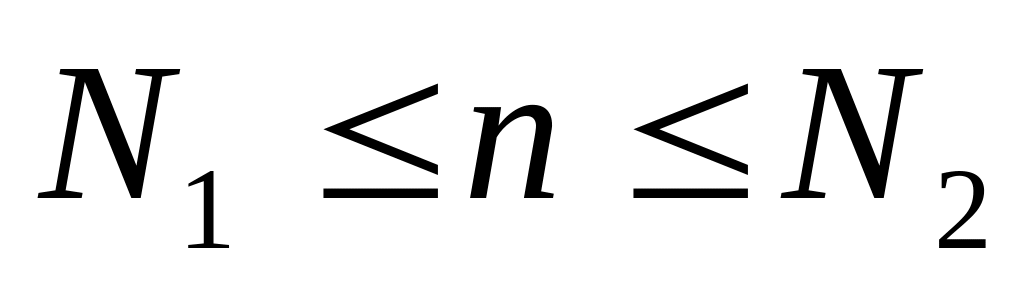де , где 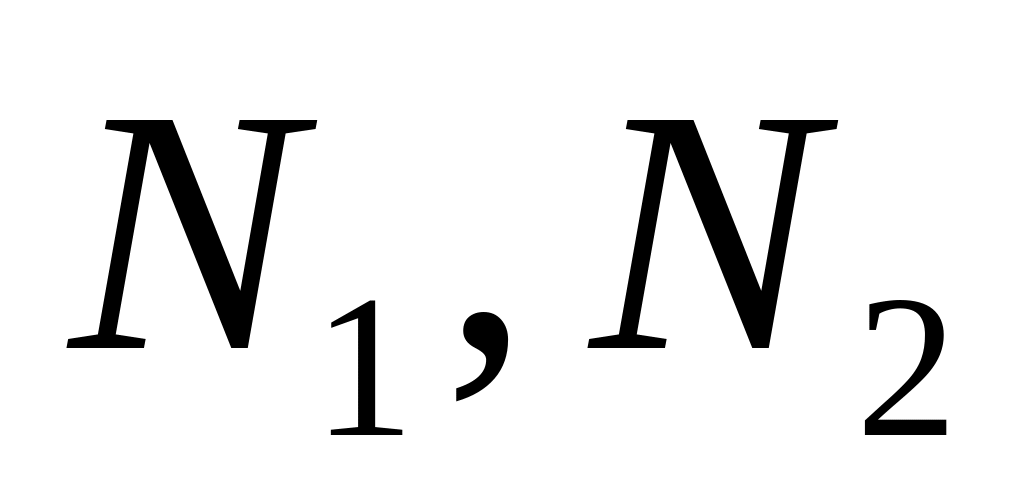-конечные отсчеты, между которыми рассматривается данный сигнал.

Цифровой сигнал представляет собой массив значений амплитуд, заданный в определенной области (N₁,N₂) c определенным интервалом дискретизации .

Каждое отдельное значение цифрового сигнала называется цифровым отсчетом. Каждый цифровой отсчет характеризуется разрядностью его представления. В зависимости от используемого АЦП количество разрядов цифрового сигнала в современных системах может колебаться от 1 до 256. Разрядность определяет максимально возможную амплитуду представляемого сигнала, которая определяется соотношением 2ⁿ-1, где n-количество разрядов.

Интервал дискретизации зависит от частоты дискретизации системы:

Интервал дискретизации для цифровых сигналов может быть равномерным или неравномерным.

Линейные системы с постоянными параметрами

Дискретная система является алгоритмом преобразования одной цифровой последовательности, называемой входной , в другую, называемую выходной . Функционально они связаны соотношением , где - функция преобразования сигнала, которые выполняет дискретная система.

Если система называется линейной, то она определяется следующим образом. Если и являются входными последовательностями, а выходными являются и , то при подаче на вход системы функции на выходе будем иметь .

Если рассмотреть систему с постоянными параметрами, то она характеризуется тем, что если входной последовательности соответствует выходная последовательность , то входной последовательности будет соответствовать выходная последовательность .

Физическая реализуемость линейной системы

Линейную систему с постоянными параметрами называют физически реализуемой, если величина выходной последовательности при зависит только от отсчетов входной последовательности с номерами .

Линейная система с постоянными параметрами называется устойчивой, если при любой ограниченной входной последовательности выходная последовательность также ограничена.

Классические методы анализа временных рядов

Временным рядом называется последовательность временных отсчетов, записанных с определенным интервалом дискретизации. Классическими методами называют методы, разработанные для анализа стационарных случайных процессов, т.е. процессов, статистические свойства которых не изменяются при переносе начала отсчета времени.

Классические методы анализа условно делятся на две группы в соответствии с целями, достигаемыми обработкой временного ряда:

1. Вероятностные методы применяются для анализа и описания статистических особенностей случайного процесса во временной области. Основными характеристиками, имеющими значение для описания статистических свойств стационарных случайных процессов являются плотность вероятности, среднее значение, дисперсия, корреляционные и ковариационные функции.

2. Параметрические и непараметрические методы спектрального анализа, которые применяются для изучения особенностей случайного процесса в частотной области. Основной характеристикой, по которой можно судить о спектральном составе исследуемого процесса является функция спектральной плотности.