3.2 Синтез контура регулирования тока якоря:

Рис. 3. Структурная схема контура тока

Его передаточная функция:

W_Р.Т(p)= ,

где k_П, Т_И, – коэффициент пропорциональной части и постоянные времени интегрирования,

Настройки вычисляются по формулам:

Т_И= ;

k_П =

W_Р.Т(p)= =0.129+1/0.796p.

5.3 Синтез контура регулирования скорости

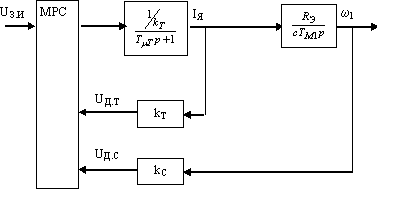
Рис. 4. Структурная схема контура регулирования скорости

Расчетные формулы:

k_T(2T_Tp+1)I_Я = - k₁ k_T I_Я- k₂ k_C₁ ;

I_Я = =

После подстановки несложно найти полином передаточной функции контура

W(p) = =

Коэффициенты полинома являются функциями параметров МРС.

Далее выбирают желаемый полином в знаменателе передаточной функции контура:

.

Приняв a₁= a₂ = 2, a₃ = 1 и Т_Ж < 0,2 t_П=0.2 , определяют настройки МРС, которые являются корнями системы уравнений:

0.00044T=0.2³

T=18.182

0.022T+0.022k₁T=2*0.2²

k₁= -0.8

0.023Tk₂=2*0.2

k₂=0.957

3.4. Структурная схема задатчика интенсивности

Рис. 5. Структурная схема задатчика интенсивности

В СУ скоростью управляющее воздействие подается через задатчик интенсивности. Приняв напряжение ограничения сумматора задатчика равным 10 В, а его коэффициент – 50, по заданному времени разгона до номинальной скорости t_П надо определяем постоянную времени интегратора ЗИ:

Т_З.И = с.

k_З.И=50.

3.5 Исследование характеристик схемы

Контур тока:

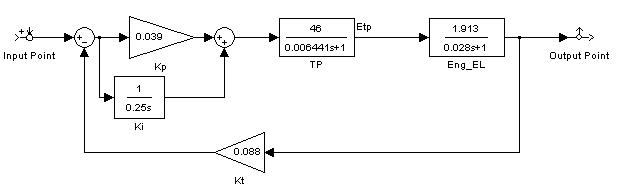
Рис. 6. Схема контура тока

В программе MATLAB был определёны коэффициенты регулятора, для соответствия переходного процесса заданному качеству.

Рис. 7. Переходной процесс в контуре тока.

Рис. 8. Диаграмма Найквиста.

Контур устойчив и обеспечивает заданное время регулирования.

Контур скорости:

Рис. 9. Схема контура скорости

Рис. 10. Переходной процесс в контуре скорости.

Рис. 11. Диаграмма Найквиста.

Система устойчива, но не обеспечивает заданное время регулирования. Поставим коэффициент усиления.

Рис. 12. Схема контура скорости

Рис. 13. Переходной процесс в контуре скорости.

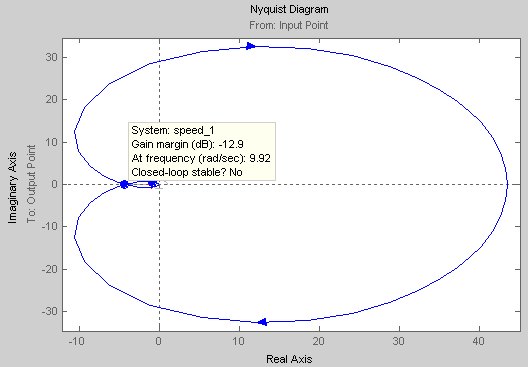
Рис. 14. Диаграмма Найквиста.

Система обеспечивает заданное время регулирования, но не устойчива. Введём корректирующее устройство с опережением по фазе:

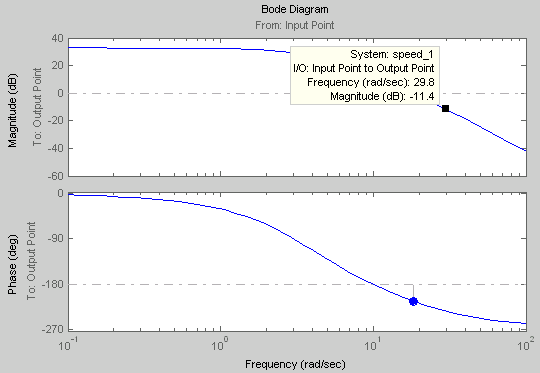
Рис. 15. Диаграмма Боде.

По диаграмме Боде (Рис.15) определим частоту, при которой амплитудная характеристика нескорректированной системы имеет значение 10log():

Передаточная функция корректирующего устройства: .

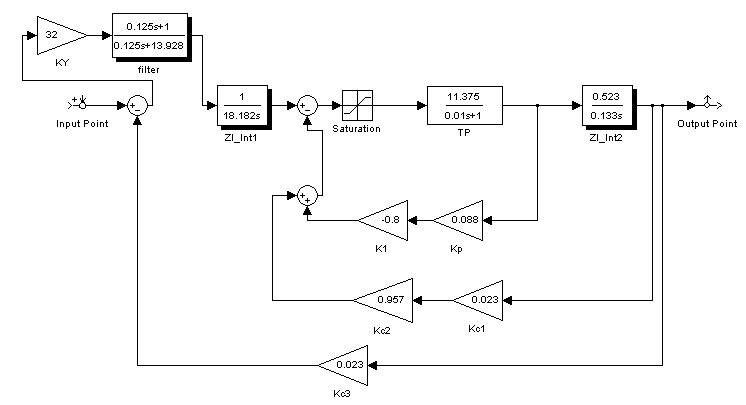
Рис. 16. Схема контура скорости

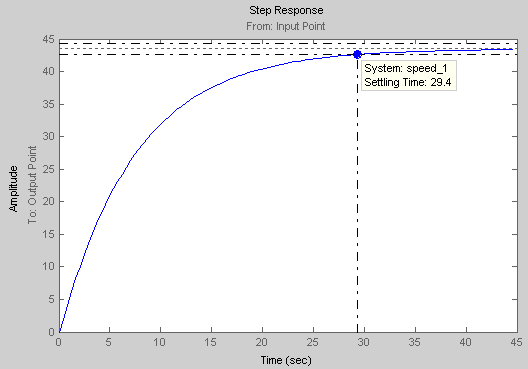
Рис. 17. Переходный процесс.

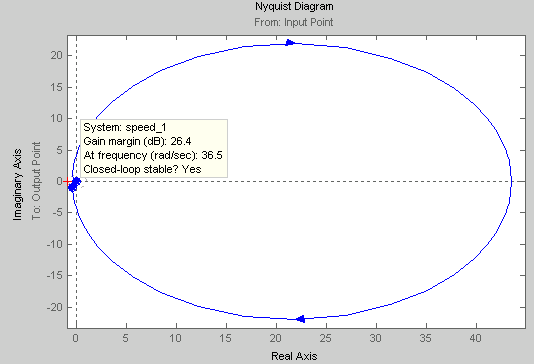
Рис. 18. Диаграмма Найквиста

Система устойчива, но не обеспечивает заданное время регулирования. Поставим коэффициент усиления.

Рис. 19. Схема контура скорости

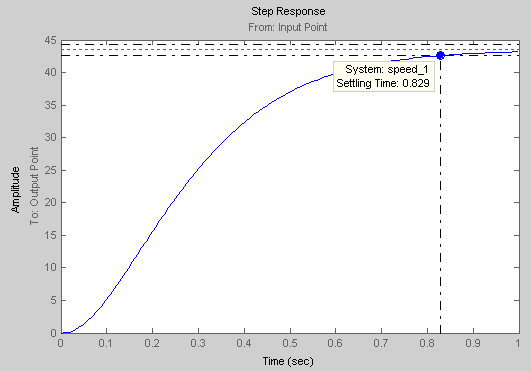
Рис. 20. Переходный процесс

Рис. 21. Диаграмма Найквиста

Система обеспечивает заданное время регулирования, но не устойчива. Введём корректирующее устройство с опережением по фазе

Рис. 22. Диаграмма Боде.

По диаграмме Боде (Рис.22) определим частоту, при которой амплитудная характеристика нескорректированной системы имеет значение 10log():

Передаточная функция корректирующего устройства:

Рис. 23. Схема контура скорости

Рис. 24. Переходный процесс

Рис. 25. Диаграмма Найквиста:

Система устойчива, но не обеспечивает заданное время регулирования. Поставим коэффициент усиления.

Рис. 24. Схема контура скорости

Рис. 25. Переходный процесс:

Рис. 26. Диаграмма Найквиста:

Система стала устойчивой и обеспечивающей заданное время регулирования

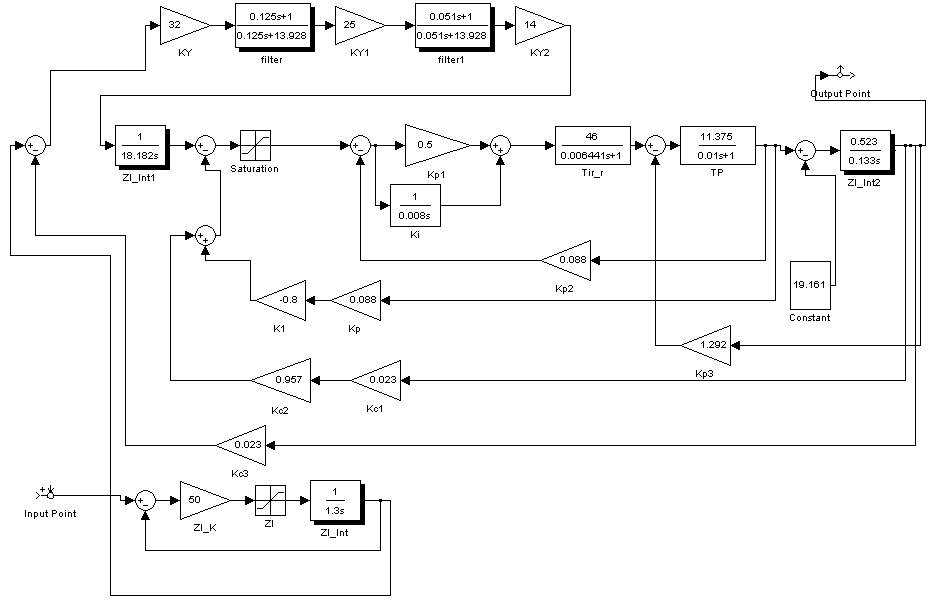
Рис. 27. Схема ЭП

Рис 28. Переходный процесс

Рис 29. Диаграмма Найквиста

Полученная система обеспечивает заданное время регулирования – 1с, выходит на установившуюся величину без перерегулирования и является устойчивой.

24