- •Тема: «Визначення відношення молярних теплоємностей газу
- •Теоретичні відомості
- •Порядок виконання
- •Контрольні питання
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні питання
- •Лабораторна робота №6 Тема: « Введення у магнетизм»
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні питання
- •Література
- •Дифракційної решітки».
- •Теоретичні відомості
- •Порядок виконання роботи.
- •Контрольні питання
- •Література
- •Теоретичні відомості
- •Контрольні питання
- •Список літератури
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні питання
- •Література
- •Тема: «Ознайомлення з роботою радіометра бета- і гама – випромінювання»
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні питання
- •Література
Лабораторна робота №11
Тема: «Визначення відношення молярних теплоємностей газу
за методом Клємана-Дезорма»
Мета роботи: Удосконалити на практиці знання законів ідеального газу.
Засвоїти сутність ізотермічного, ізохорного, ізобарного та адіабатного процесів, а також понять теплоємності ідеального газу при постійному тискові та постійному об’ємі, понять кількості степенів вільності молекули, внутрішньої енергії ідеального газу, основного закону термодинаміки.
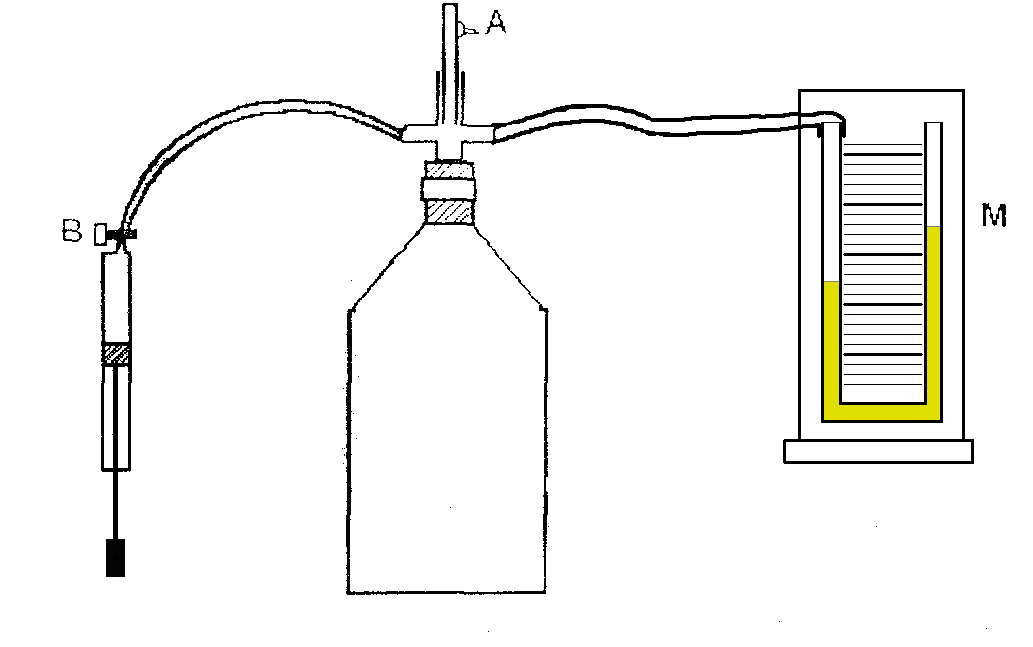
Прилади та обладнання: прилад Клємана-Дезорма, манометр, насос, фізичні таблиці.
Теоретичні відомості
Питомою теплоємністю газу називається величина, чисельно рівна кількості теплоти, яку необхідно надати одиниці маси газу, для того, щоб збільшити його температуру на один градус. Для газів ця величина залежить від умов, при яких здійснюється підігрів. Можна проводити підігрів при постійному об'ємі чи при постійному тиску. Тоді отримаємо відповідно питому теплоємність газу при постійному об'ємі сv чи при постійному тиску ср , при цьому ср завжди більше ніж сv .Це пояснюється тим, що для підігріву газу з постійним об'ємом уся кількість теплоти йде тільки на збільшення внутрішньої енергії газу; а при підігріві газу з постійним тиском, окрім теплоти, яка йде на збільшення внутрішньої енергії газу, необхідно ще тепло для роботи розширення газу.
Безпосереднє визначення ср та сv важке, оскільки теплоємність газу мaла у порівнянні з теплоємністю сосуду. Простіше визначити відношення цих теплоємностей:
![]()
Величина γ має велике значення у термодинаміці. Вона входить у рівняння Пуассона, що описує адіабатичні процеси:
рVγ = const
Адіабатичним процесом називається така зміна стану газу, яка проходить без теплообміну з навколишнім середовищем. Тоді перший закон термодинаміки для адіабатичного процесу розширення прийме вигляд:
dU+dA=0 або dA = – dU
Отже робота розширення газу при такому процесі буде здійснюватися за рахунок внутрішньої енергії газу. Оскільки внутрішня енергія газу прямо пропорційна його абсолютній температурі то після здійснення адіабатичного процесу розширення температура газу знижується.
Запропонований Клєманом та Дезормом метод полягає у наступному. Якщо у скляний балон, з’єднаний з манометром, за допомогою насосу закачати повітря, то тиск у балоні буде вище за атмосферний. Після того, як повітря у балоні прийме температуру навколишнього повітря Т1 , тиск у балоні буде Р1 :
P1 = P2 + bh1, (1)
де Р2 - атмосферний тиск, h1 - різниця рівнів рідини у манометрі, b – коефі-цієнт переходу від різниці рівнів манометру у см до тиску, що вимірюється у паскалях (Па) за системою СІ. Цей стан газу з параметрами Р1 Т1 V1 будемо вважати початковим.
Швидке розширення газу можна з достатнім наближенням розглядати як адіабатичне. Якщо за короткий час (десь 0,5 с) газ розширити, – з’єднавши з атмосферним, то тиск у балоні знизиться до атмосферного. Газ перейде у новий стан, що характеризується величинами
Р2 Т2 V2. Температура газу T2 після адіабатичного розширення буде менша ніж навколишня внаслідок зменшення внутрішньої енергії газу. Саме за рахунок внутрішньої енергії газу і була здійснена робота розширення А. Параметри початкового і нового стану газу пов'язані рівнянням Пуассона для адіабатичного процесу:
![]() (2)
(2)
Через 3-5 хв. газ нагріється до температури навколишнього повітря. Оскільки при цьому підігріві об’єм газу залишається незмінним, то тиск збільшиться до Р3 ізобарно.. При цьому
Р3 = Р2 + bh2 , (3)
де h2-різниця рівнів на манометру. Кінцевий стан газу характеризується параметрами Р3 Т1 V2 . Вихідний і кінцевий стан газу знаходиться при одній і тій самій температурі. Тому за законом Бойля-Маріотта для ізотер-мічного процесу маємо:
Р3 V2=Р1 V1 (4)
Піднесемо рівняння (4) до степеня γ та розділимо його почленно на рівнян-ня (2):
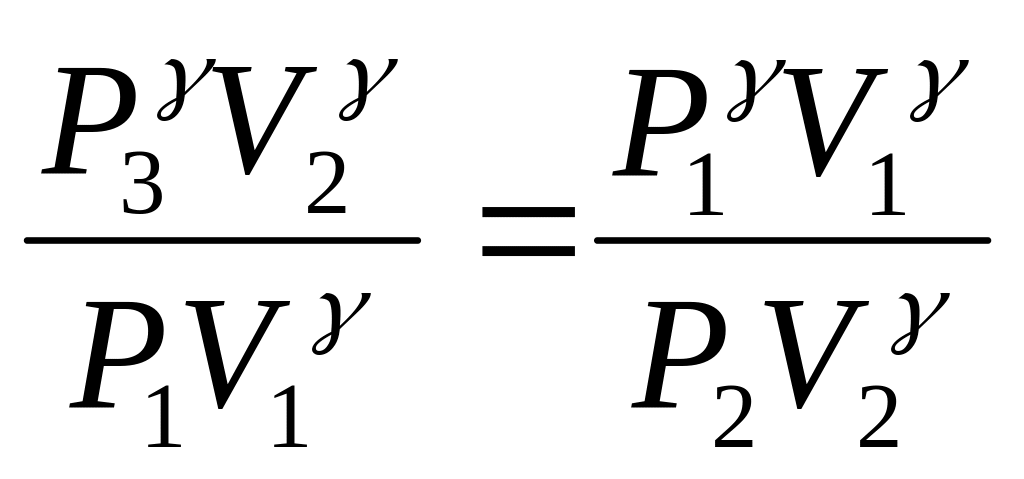 ;
;
![]()
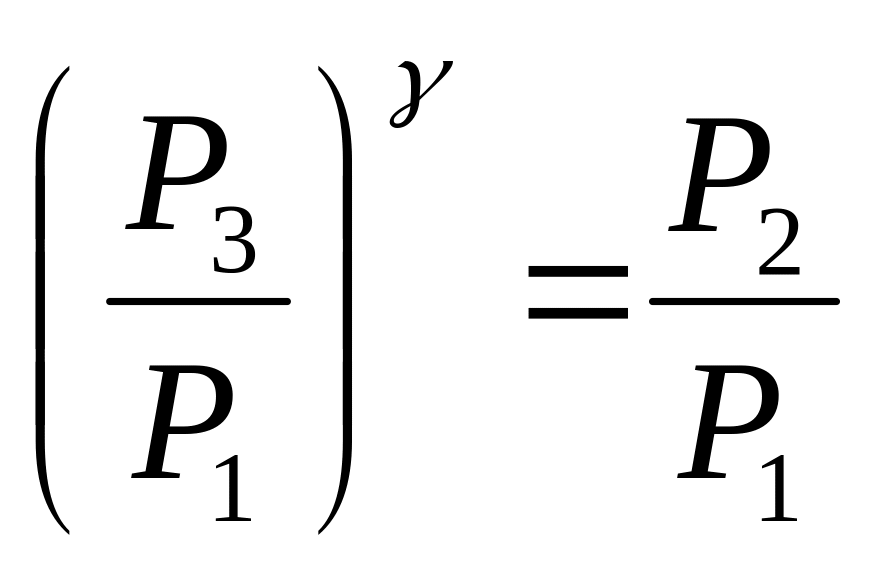 (5)
(5)
Логарифмуючи рівняння (5), знаходимо:
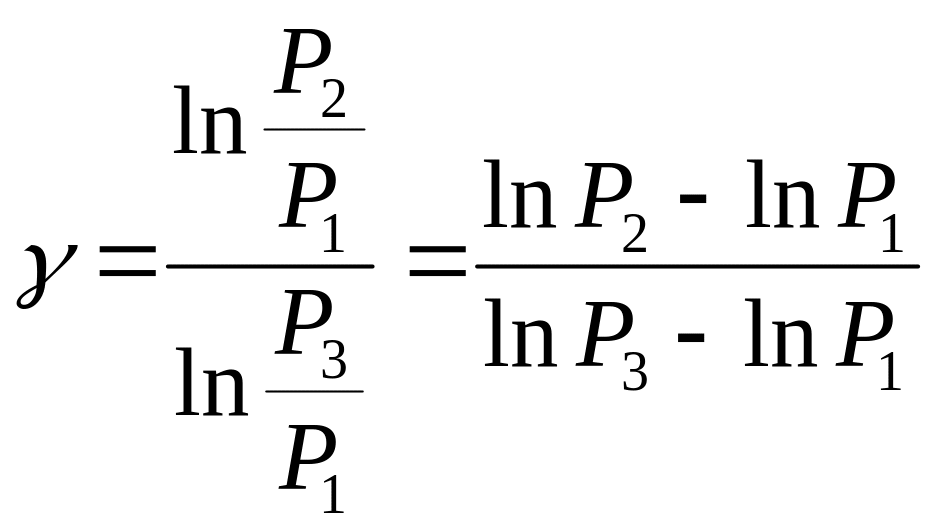 (6)
(6)
Тиски P1, P2, Р3 відрізняються незначно, тому різницю логарифмів можна замінити різницею самих чисел тобто:
![]()
Підставивши Р1 та Р3 з виразів (1) та (3) остаточно отримуємо:
![]() (7)
За
цією формулою і визначається відношення
питомих тепло-
(7)
За
цією формулою і визначається відношення
питомих тепло-
ємностей ідеального газу за методом Клємана - Дезорма.