Контрольные вопросы

1. Покажите, что в условиях опыта концентрацию газов можно считать постоянной по всему объему сосуда V₂ (и V₁).

2. Почему следует ожидать, что график зависимости D от 1/Р должен иметь вид прямой линии?

3. От каких параметров зависит коэффициент диффузии?

4. Охарактеризуйте применяемый в работе метод измерения коэффициента взаимной диффузии газов.

5. Почему вблизи поверхности датчика происходит температурный скачок?

6. Какие еще явления переноса Вы знаете? Какая связь существует между коэффициентами переноса?

Лабораторная работа №9

ЭФФЕКТ ДЖОУЛЯ-ТОМСОНА

Цель работы: Овладеть методикой определения коэффи­циента Джоуля-Томсона. Определить коэффициент Джоуля-Томсона и его зависимость от температуры.

Литература:

1. Кикоин А.К., Кикоин И.К. Молекулярная физика. — М.: Наука, 1976, гл. III, § 111.

2. Сивухин Д.В. Общий курс физики. Т.2. Термодинамика и молекулярная физика — М.: Наука, 1990, §§ 97, 98, 104.

3. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. I. Физические основы механики. Молекулярная физика. Колебания и волны. – М.: Физматгиз, 1961, гл. VII, §§ 64, 65.

4. Лабораторные занятия по физике. /Под ред. Гольдина Л.Л. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 704 с.

5. Введение в технику эксперимента/ Составитель: Беленко И.А. –   БелГУ, 2004. – 124 с.

Приборы, оборудование и их характеристики:

1. Трубка с пористой перегородкой;

2. Термостат TW – 2.03;

3. Дифференциальная термопара медь – константан;

4. Цифровой вольтметр В7 – 46/1;

5. Форвакуумный насос 3НВР – 1Д.

Теория метода

Эффектом Джоуля — Томсона называется изменение температуры газа, медленно протекающего из области высокого в область низкого давления через пористую перегородку в условиях хорошей тепловой изоляции. В разреженных га­зах, которые приближаются по своим свойствам к идеальному газу, при таком течении температура газа не меняется. Эффект Джоуля — Томсона демонстрирует отличие исследуемого газа от идеального.

Коэффициентом Джоуля–Томсона называется отношение

,

где – изменение температуры при течении газа из одной области в другую, перепад давлений между которыми .

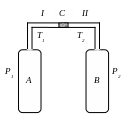
Рис. 1. Опыт Джоуля-Томсона.

Рассмотрим стационарный поток газа между произвольными сече­ниями I и II трубки (до пористой перегородки С и после нее), соединяющей сосуды А и В (рис. 1). Пусть, для опреде­ленности, через трубку прошел 1 моль газа;  – его масса. Молярные объемы газа, его давления и отнесенные к молю внутрен­ние энергии газа в сечениях I и II обозначим соответственно V₁, P₁, U₁ и V₂, Р₂, U₂. Для того чтобы ввести в трубку объем V₁, над газом нуж­но совершить работу А₁=P₁V₁. Проходя через сечение II, газ сам со­вершает работу A₂=Р₂ V₂. Если трубка окружена теплоизолирующим веществом, то через боковые стенки не происходит ни обмен теплом, ни передача механической энергии и

. (1)

В уравнении (1) учтено изменение как внутренней (первые члены в скобках), так и кинетической (вторые члены в скобках) энергии газа. Подставляя в (1) написанные выражения для А₁ и А₂ и перегруппиро­вывая члены, найдем

H₁ –H₂ =(U₁ + P₁V₁) – (U₂ + P₂V₂) = (2)

Входящая в это выражение величина

H = U +PV. (3)

носит название энтальпии. Формула (2) полностью описывает про­цесс стационарного течения газа.

Сделаем несколько замечаний. Прежде всего, отметим, что при процессе Джоуля – Томсона газ испытывает в пористой перегородке существенное трение, приводящее к ее нагреву. Потери энергии на нагрев трубки в начале процесса могут быть очень существенными и сильно искажают ход явления. После того как температура трубки установится и газ станет уносить с собой все выделенное им в перегородке тепло, формула (1) становится точной, — если, конечно, теплоизоля­ция трубки достаточно хороша и не происходит утечек тепла наружу через ее стенки.

Второе замечание связано с правой частью (2). Процесс Джоуля — Томсона в чистом виде осуществляется лишь в том случае, если пра­вой частью можно пренебречь, т.е. если скорость газа с обеих сторон трубки достаточно мала. У нас сейчас нет критерия, который позво­лил бы установить, когда это можно сделать. Поэтому мы отложим на некоторое время обсуждение вопроса о правой части (2), а пока бу­дем считать, что энтальпия газа не меняется, т. е.

H₁ =H₂. (4)

Рассмотрим эффект Джоуля — Томсона в идеаль­ном газе. Для идеального газа внутренняя энергия U является функ­цией одной только температуры. Произведение РV равно RТ и тоже зависит только от температуры. Поэтому и энтальпия идеального газа зависит от одной только температуры. При процессе Джоуля — Том­сона энтальпия, а значит и температура идеального газа, не меняется. Поэтому, как уже указывалось, изменение температуры в рассматриваемом процессе и является чувствительным индикатором, указывающим на отличие реальных газов от идеального.

Заметим теперь, что энтальпия газа, подобно его энергии, объему и давлению, является функцией состояния. Это означает, что, вычис­ляя изменение энтальпии при переходе от сечения I к сечению II, нет нужды детально следить за ходом процесса Джоуля — Томсона, что сделать очень непросто, так как процесс протекания газа через пористую перегородку не может быть рассчитан простыми методами. Вме­сто этого можно рассчитать изменение энтальпии при любом другом процессе, происходящем между тем же начальным и конеч­ным состояниями. Выберем для расчета обратимый процесс, для ко­торого нетрудно написать точные формулы.

При дальнейшем рассмотрении мы ограничимся малыми перепа­дами Р и, иначе говоря, будем рассматривать дифференциальный эффект Джоуля–Томсона. Выберем в качестве независимых пере­менных давление и температуру. Тогда

.¹ (5)

Коэффициент Джоуля — Томсона , следовательно, равен

(6)

Рассмотрим производные, входящие в эту формулу. Заметим, что в силу первого закона термодинамики

Q = dU + PdV = d(U + PV) – VdP = dH – VdP.

Рассмотрим процесс при постоянном Р. Тогда второй член формулы обращается в нуль. Разделим обе части формулы на dT:

(Q/dT)_p = (dH/dT)_p.

Левая часть этого равенства (по определению) равна теплоемкости при постоянном давлении С_Р. Поэтому

(7)

Можно показать (см. приложение 6), что

. (8)

Поэтому

. (9)